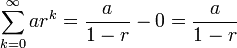Let's say we have 0.33, we need to output 1/3.
If we have 0.4, we need to output 2/5.
The idea is to make it human-readable to make the user understand "x parts out of y" as a better way of understanding data.
I know that percentages is a good substitute but I was wondering if there was a simple way to do this?
I have found David Eppstein's find rational approximation to given real number C code to be exactly what you are asking for. Its based on the theory of continued fractions and very fast and fairly compact.
I have used versions of this customized for specific numerator and denominator limits.
/*
** find rational approximation to given real number
** David Eppstein / UC Irvine / 8 Aug 1993
**
** With corrections from Arno Formella, May 2008
**
** usage: a.out r d
** r is real number to approx
** d is the maximum denominator allowed
**
** based on the theory of continued fractions
** if x = a1 + 1/(a2 + 1/(a3 + 1/(a4 + ...)))
** then best approximation is found by truncating this series
** (with some adjustments in the last term).
**
** Note the fraction can be recovered as the first column of the matrix
** ( a1 1 ) ( a2 1 ) ( a3 1 ) ...
** ( 1 0 ) ( 1 0 ) ( 1 0 )
** Instead of keeping the sequence of continued fraction terms,
** we just keep the last partial product of these matrices.
*/
#include <stdio.h>
main(ac, av)
int ac;
char ** av;
{
double atof();
int atoi();
void exit();
long m[2][2];
double x, startx;
long maxden;
long ai;
/* read command line arguments */
if (ac != 3) {
fprintf(stderr, "usage: %s r d\n",av[0]); // AF: argument missing
exit(1);
}
startx = x = atof(av[1]);
maxden = atoi(av[2]);
/* initialize matrix */
m[0][0] = m[1][1] = 1;
m[0][1] = m[1][0] = 0;
/* loop finding terms until denom gets too big */
while (m[1][0] * ( ai = (long)x ) + m[1][1] <= maxden) {
long t;
t = m[0][0] * ai + m[0][1];
m[0][1] = m[0][0];
m[0][0] = t;
t = m[1][0] * ai + m[1][1];
m[1][1] = m[1][0];
m[1][0] = t;
if(x==(double)ai) break; // AF: division by zero
x = 1/(x - (double) ai);
if(x>(double)0x7FFFFFFF) break; // AF: representation failure
}
/* now remaining x is between 0 and 1/ai */
/* approx as either 0 or 1/m where m is max that will fit in maxden */
/* first try zero */
printf("%ld/%ld, error = %e\n", m[0][0], m[1][0],
startx - ((double) m[0][0] / (double) m[1][0]));
/* now try other possibility */
ai = (maxden - m[1][1]) / m[1][0];
m[0][0] = m[0][0] * ai + m[0][1];
m[1][0] = m[1][0] * ai + m[1][1];
printf("%ld/%ld, error = %e\n", m[0][0], m[1][0],
startx - ((double) m[0][0] / (double) m[1][0]));
}
From Python 2.6 on there is the fractions module.
(Quoting from the docs.)
>>> from fractions import Fraction
>>> Fraction('3.1415926535897932').limit_denominator(1000)
Fraction(355, 113)
>>> from math import pi, cos
>>> Fraction.from_float(cos(pi/3))
Fraction(4503599627370497, 9007199254740992)
>>> Fraction.from_float(cos(pi/3)).limit_denominator()
Fraction(1, 2)
If the the output is to give a human reader a fast impression of the order of the result, it makes no sense return something like "113/211", so the output should limit itself to using one-digit numbers (and maybe 1/10 and 9/10). If so, you can observe that there are only 27 different fractions.
Since the underlying math for generating the output will never change, a solution could be to simply hard-code a binary search tree, so that the function would perform at most log(27) ~= 4 3/4 comparisons. Here is a tested C version of the code
char *userTextForDouble(double d, char *rval)
{
if (d == 0.0)
return "0";
// TODO: negative numbers:if (d < 0.0)...
if (d >= 1.0)
sprintf(rval, "%.0f ", floor(d));
d = d-floor(d); // now only the fractional part is left
if (d == 0.0)
return rval;
if( d < 0.47 )
{
if( d < 0.25 )
{
if( d < 0.16 )
{
if( d < 0.12 ) // Note: fixed from .13
{
if( d < 0.11 )
strcat(rval, "1/10"); // .1
else
strcat(rval, "1/9"); // .1111....
}
else // d >= .12
{
if( d < 0.14 )
strcat(rval, "1/8"); // .125
else
strcat(rval, "1/7"); // .1428...
}
}
else // d >= .16
{
if( d < 0.19 )
{
strcat(rval, "1/6"); // .1666...
}
else // d > .19
{
if( d < 0.22 )
strcat(rval, "1/5"); // .2
else
strcat(rval, "2/9"); // .2222...
}
}
}
else // d >= .25
{
if( d < 0.37 ) // Note: fixed from .38
{
if( d < 0.28 ) // Note: fixed from .29
{
strcat(rval, "1/4"); // .25
}
else // d >=.28
{
if( d < 0.31 )
strcat(rval, "2/7"); // .2857...
else
strcat(rval, "1/3"); // .3333...
}
}
else // d >= .37
{
if( d < 0.42 ) // Note: fixed from .43
{
if( d < 0.40 )
strcat(rval, "3/8"); // .375
else
strcat(rval, "2/5"); // .4
}
else // d >= .42
{
if( d < 0.44 )
strcat(rval, "3/7"); // .4285...
else
strcat(rval, "4/9"); // .4444...
}
}
}
}
else
{
if( d < 0.71 )
{
if( d < 0.60 )
{
if( d < 0.55 ) // Note: fixed from .56
{
strcat(rval, "1/2"); // .5
}
else // d >= .55
{
if( d < 0.57 )
strcat(rval, "5/9"); // .5555...
else
strcat(rval, "4/7"); // .5714
}
}
else // d >= .6
{
if( d < 0.62 ) // Note: Fixed from .63
{
strcat(rval, "3/5"); // .6
}
else // d >= .62
{
if( d < 0.66 )
strcat(rval, "5/8"); // .625
else
strcat(rval, "2/3"); // .6666...
}
}
}
else
{
if( d < 0.80 )
{
if( d < 0.74 )
{
strcat(rval, "5/7"); // .7142...
}
else // d >= .74
{
if(d < 0.77 ) // Note: fixed from .78
strcat(rval, "3/4"); // .75
else
strcat(rval, "7/9"); // .7777...
}
}
else // d >= .8
{
if( d < 0.85 ) // Note: fixed from .86
{
if( d < 0.83 )
strcat(rval, "4/5"); // .8
else
strcat(rval, "5/6"); // .8333...
}
else // d >= .85
{
if( d < 0.87 ) // Note: fixed from .88
{
strcat(rval, "6/7"); // .8571
}
else // d >= .87
{
if( d < 0.88 ) // Note: fixed from .89
{
strcat(rval, "7/8"); // .875
}
else // d >= .88
{
if( d < 0.90 )
strcat(rval, "8/9"); // .8888...
else
strcat(rval, "9/10"); // .9
}
}
}
}
}
}
return rval;
}
Here's a link explaining the math behind converting a decimal to a fraction:
http://www.webmath.com/dec2fract.html
And here's an example function for how to actually do it using VB (from www.freevbcode.com/ShowCode.asp?ID=582):
Public Function Dec2Frac(ByVal f As Double) As String
Dim df As Double
Dim lUpperPart As Long
Dim lLowerPart As Long
lUpperPart = 1
lLowerPart = 1
df = lUpperPart / lLowerPart
While (df <> f)
If (df < f) Then
lUpperPart = lUpperPart + 1
Else
lLowerPart = lLowerPart + 1
lUpperPart = f * lLowerPart
End If
df = lUpperPart / lLowerPart
Wend
Dec2Frac = CStr(lUpperPart) & "/" & CStr(lLowerPart)
End Function
(From google searches: convert decimal to fraction, convert decimal to fraction code)
You might want to read What Every Computer Scientist Should Know about Floating Point Arithmetic.
You'll have to specify some precision by multiplying by a large number:
3.141592 * 1000000 = 3141592
then you can make a fraction:
3 + (141592 / 1000000)
and reduce via GCD...
3 + (17699 / 125000)
but there is no way to get the intended fraction out. You might want to always use fractions throughout your code instead --just remember to reduce fractions when you can to avoid overflow!
Here are Perl and Javascript versions of the VB code suggested by devinmoore:
Perl:
sub dec2frac {
my $d = shift;
my $df = 1;
my $top = 1;
my $bot = 1;
while ($df != $d) {
if ($df < $d) {
$top += 1;
}
else {
$bot += 1;
$top = int($d * $bot);
}
$df = $top / $bot;
}
return "$top/$bot";
}
And the almost identical javascript:
function dec2frac(d) {
var df = 1;
var top = 1;
var bot = 1;
while (df != d) {
if (df < d) {
top += 1;
}
else {
bot += 1;
top = parseInt(d * bot);
}
df = top / bot;
}
return top + '/' + bot;
}
//Put in your test number here:
var floatNumber = 2.56;
alert(floatNumber + " = " + dec2frac(floatNumber));A C# implementation
/// <summary>
/// Represents a rational number
/// </summary>
public struct Fraction
{
public int Numerator;
public int Denominator;
/// <summary>
/// Constructor
/// </summary>
public Fraction(int numerator, int denominator)
{
this.Numerator = numerator;
this.Denominator = denominator;
}
/// <summary>
/// Approximates a fraction from the provided double
/// </summary>
public static Fraction Parse(double d)
{
return ApproximateFraction(d);
}
/// <summary>
/// Returns this fraction expressed as a double, rounded to the specified number of decimal places.
/// Returns double.NaN if denominator is zero
/// </summary>
public double ToDouble(int decimalPlaces)
{
if (this.Denominator == 0)
return double.NaN;
return System.Math.Round(
Numerator / (double)Denominator,
decimalPlaces
);
}
/// <summary>
/// Approximates the provided value to a fraction.
/// http://stackoverflow.com/questions/95727/how-to-convert-floats-to-human-readable-fractions
/// </summary>
private static Fraction ApproximateFraction(double value)
{
const double EPSILON = .000001d;
int n = 1; // numerator
int d = 1; // denominator
double fraction = n / d;
while (System.Math.Abs(fraction - value) > EPSILON)
{
if (fraction < value)
{
n++;
}
else
{
d++;
n = (int)System.Math.Round(value * d);
}
fraction = n / (double)d;
}
return new Fraction(n, d);
}
}
The Stern-Brocot Tree induces a fairly natural way to approximate real numbers by fractions with simple denominators.
Part of the problem is that so many fractions aren't actually easily construed as fractions. E.g. 0.33 isn't 1/3, it's 33/100. But if you remember your elementary school training, then there is a process of converting decimal values into fractions, however it's unlikely to give you what you want since most of the time decimal numbers aren't stored at 0.33, but 0.329999999999998 or some such.
Do yourself a favor and don't bother with this, but if you need to then you can do the following:
Multiply the original value by 10 until you remove the fractional part. Keep that number, and use it as the divisor. Then do a series of simplifications by looking for common denominators.
So 0.4 would be 4/10. You would then look for common divisors starting with low values, probably prime numbers. Starting with 2, you would see if 2 divides both the numerator and denominator evenly by checking if the floor of division is the same as the division itself.
floor(5/2) = 2
5/2 = 2.5
So 5 does not divide 2 evenly. So then you check the next number, say 3. You do this until you hit at or above the square root of the smaller number.
After you do that then you need
This is not an "algorithm", just a Python solution: http://docs.python.org/library/fractions.html
>>> from fractions import Fraction
>>> Fraction('3.1415926535897932').limit_denominator(1000)
Fraction(355, 113)
This algorithm by Ian Richards / John Kennedy not only returns nice fractions, it also performs very well in terms of speed. This is C# code as taken from this answer by me.
It can handle all double values except special values like NaN and +/- infinity, which you'll have to add if needed.
It returns a new Fraction(numerator, denominator). Replace by your own type.
For more example values and a comparison with other algorithms, go here
public Fraction RealToFraction(double value, double accuracy)
{
if (accuracy <= 0.0 || accuracy >= 1.0)
{
throw new ArgumentOutOfRangeException("accuracy", "Must be > 0 and < 1.");
}
int sign = Math.Sign(value);
if (sign == -1)
{
value = Math.Abs(value);
}
// Accuracy is the maximum relative error; convert to absolute maxError
double maxError = sign == 0 ? accuracy : value * accuracy;
int n = (int) Math.Floor(value);
value -= n;
if (value < maxError)
{
return new Fraction(sign * n, 1);
}
if (1 - maxError < value)
{
return new Fraction(sign * (n + 1), 1);
}
double z = value;
int previousDenominator = 0;
int denominator = 1;
int numerator;
do
{
z = 1.0 / (z - (int) z);
int temp = denominator;
denominator = denominator * (int) z + previousDenominator;
previousDenominator = temp;
numerator = Convert.ToInt32(value * denominator);
}
while (Math.Abs(value - (double) numerator / denominator) > maxError && z != (int) z);
return new Fraction((n * denominator + numerator) * sign, denominator);
}
Example values returned by this algorithm:
Accuracy: 1.0E-3 | Richards
Input | Result Error
======================| =============================
3 | 3/1 0
0.999999 | 1/1 1.0E-6
1.000001 | 1/1 -1.0E-6
0.50 (1/2) | 1/2 0
0.33... (1/3) | 1/3 0
0.67... (2/3) | 2/3 0
0.25 (1/4) | 1/4 0
0.11... (1/9) | 1/9 0
0.09... (1/11) | 1/11 0
0.62... (307/499) | 8/13 2.5E-4
0.14... (33/229) | 16/111 2.7E-4
0.05... (33/683) | 10/207 -1.5E-4
0.18... (100/541) | 17/92 -3.3E-4
0.06... (33/541) | 5/82 -3.7E-4
0.1 | 1/10 0
0.2 | 1/5 0
0.3 | 3/10 0
0.4 | 2/5 0
0.5 | 1/2 0
0.6 | 3/5 0
0.7 | 7/10 0
0.8 | 4/5 0
0.9 | 9/10 0
0.01 | 1/100 0
0.001 | 1/1000 0
0.0001 | 1/10000 0
0.33333333333 | 1/3 1.0E-11
0.333 | 333/1000 0
0.7777 | 7/9 1.0E-4
0.11 | 10/91 -1.0E-3
0.1111 | 1/9 1.0E-4
3.14 | 22/7 9.1E-4
3.14... (pi) | 22/7 4.0E-4
2.72... (e) | 87/32 1.7E-4
0.7454545454545 | 38/51 -4.8E-4
0.01024801004 | 2/195 8.2E-4
0.99011 | 100/101 -1.1E-5
0.26... (5/19) | 5/19 0
0.61... (37/61) | 17/28 9.7E-4
|
Accuracy: 1.0E-4 | Richards
Input | Result Error
======================| =============================
0.62... (307/499) | 299/486 -6.7E-6
0.05... (33/683) | 23/476 6.4E-5
0.06... (33/541) | 33/541 0
1E-05 | 1/99999 1.0E-5
0.7777 | 1109/1426 -1.8E-7
3.14... (pi) | 333/106 -2.6E-5
2.72... (e) | 193/71 1.0E-5
0.61... (37/61) | 37/61 0
"Let's say we have 0.33, we need to output "1/3". "
What precision do you expect the "solution" to have? 0.33 is not equal to 1/3. How do you recognize a "good" (easy to read) answer?
No matter what, a possible algorithm could be:
If you expect to find a nearest fraction in a form X/Y where Y is less then 10, then you can loop though all 9 possible Ys, for each Y compute X, and then select the most accurate one.
A built-in solution in R:
library(MASS)
fractions(0.666666666)
## [1] 2/3
This uses a continued fraction method and has optional cycles and max.denominator arguments for adjusting the precision.
You can do this in any programming language using the following steps:
Example: 0.2 =0.2 x 10^1/10^1 =2/10 =1/5
So, that can be read as '1 part out of 5'
Let's say we have 0.33, we need to output "1/3". If we have "0.4", we need to output "2/5".
It's wrong in common case, because of 1/3 = 0.3333333 = 0.(3) Moreover, it's impossible to find out from suggested above solutions is decimal can be converted to fraction with defined precision, because output is always fraction.
BUT, i suggest my comprehensive function with many options based on idea of Infinite geometric series, specifically on formula:
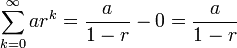
At first this function is trying to find period of fraction in string representation. After that described above formula is applied.
Rational numbers code is borrowed from Stephen M. McKamey rational numbers implementation in C#. I hope there is not very hard to port my code on other languages.
/// <summary>
/// Convert decimal to fraction
/// </summary>
/// <param name="value">decimal value to convert</param>
/// <param name="result">result fraction if conversation is succsess</param>
/// <param name="decimalPlaces">precision of considereation frac part of value</param>
/// <param name="trimZeroes">trim zeroes on the right part of the value or not</param>
/// <param name="minPeriodRepeat">minimum period repeating</param>
/// <param name="digitsForReal">precision for determination value to real if period has not been founded</param>
/// <returns></returns>
public static bool FromDecimal(decimal value, out Rational<T> result,
int decimalPlaces = 28, bool trimZeroes = false, decimal minPeriodRepeat = 2, int digitsForReal = 9)
{
var valueStr = value.ToString("0.0000000000000000000000000000", CultureInfo.InvariantCulture);
var strs = valueStr.Split('.');
long intPart = long.Parse(strs[0]);
string fracPartTrimEnd = strs[1].TrimEnd(new char[] { '0' });
string fracPart;
if (trimZeroes)
{
fracPart = fracPartTrimEnd;
decimalPlaces = Math.Min(decimalPlaces, fracPart.Length);
}
else
fracPart = strs[1];
result = new Rational<T>();
try
{
string periodPart;
bool periodFound = false;
int i;
for (i = 0; i < fracPart.Length; i++)
{
if (fracPart[i] == '0' && i != 0)
continue;
for (int j = i + 1; j < fracPart.Length; j++)
{
periodPart = fracPart.Substring(i, j - i);
periodFound = true;
decimal periodRepeat = 1;
decimal periodStep = 1.0m / periodPart.Length;
var upperBound = Math.Min(fracPart.Length, decimalPlaces);
int k;
for (k = i + periodPart.Length; k < upperBound; k += 1)
{
if (periodPart[(k - i) % periodPart.Length] != fracPart[k])
{
periodFound = false;
break;
}
periodRepeat += periodStep;
}
if (!periodFound && upperBound - k <= periodPart.Length && periodPart[(upperBound - i) % periodPart.Length] > '5')
{
var ind = (k - i) % periodPart.Length;
var regroupedPeriod = (periodPart.Substring(ind) + periodPart.Remove(ind)).Substring(0, upperBound - k);
ulong periodTailPlusOne = ulong.Parse(regroupedPeriod) + 1;
ulong fracTail = ulong.Parse(fracPart.Substring(k, regroupedPeriod.Length));
if (periodTailPlusOne == fracTail)
periodFound = true;
}
if (periodFound && periodRepeat >= minPeriodRepeat)
{
result = FromDecimal(strs[0], fracPart.Substring(0, i), periodPart);
break;
}
else
periodFound = false;
}
if (periodFound)
break;
}
if (!periodFound)
{
if (fracPartTrimEnd.Length >= digitsForReal)
return false;
else
{
result = new Rational<T>(long.Parse(strs[0]), 1, false);
if (fracPartTrimEnd.Length != 0)
result = new Rational<T>(ulong.Parse(fracPartTrimEnd), TenInPower(fracPartTrimEnd.Length));
return true;
}
}
return true;
}
catch
{
return false;
}
}
public static Rational<T> FromDecimal(string intPart, string fracPart, string periodPart)
{
Rational<T> firstFracPart;
if (fracPart != null && fracPart.Length != 0)
{
ulong denominator = TenInPower(fracPart.Length);
firstFracPart = new Rational<T>(ulong.Parse(fracPart), denominator);
}
else
firstFracPart = new Rational<T>(0, 1, false);
Rational<T> secondFracPart;
if (periodPart != null && periodPart.Length != 0)
secondFracPart =
new Rational<T>(ulong.Parse(periodPart), TenInPower(fracPart.Length)) *
new Rational<T>(1, Nines((ulong)periodPart.Length), false);
else
secondFracPart = new Rational<T>(0, 1, false);
var result = firstFracPart + secondFracPart;
if (intPart != null && intPart.Length != 0)
{
long intPartLong = long.Parse(intPart);
result = new Rational<T>(intPartLong, 1, false) + (intPartLong == 0 ? 1 : Math.Sign(intPartLong)) * result;
}
return result;
}
private static ulong TenInPower(int power)
{
ulong result = 1;
for (int l = 0; l < power; l++)
result *= 10;
return result;
}
private static decimal TenInNegPower(int power)
{
decimal result = 1;
for (int l = 0; l > power; l--)
result /= 10.0m;
return result;
}
private static ulong Nines(ulong power)
{
ulong result = 9;
if (power >= 0)
for (ulong l = 0; l < power - 1; l++)
result = result * 10 + 9;
return result;
}
There are some examples of usings:
Rational<long>.FromDecimal(0.33333333m, out r, 8, false);
// then r == 1 / 3;
Rational<long>.FromDecimal(0.33333333m, out r, 9, false);
// then r == 33333333 / 100000000;
Your case with right part zero part trimming:
Rational<long>.FromDecimal(0.33m, out r, 28, true);
// then r == 1 / 3;
Rational<long>.FromDecimal(0.33m, out r, 28, true);
// then r == 33 / 100;
Min period demostration:
Rational<long>.FromDecimal(0.123412m, out r, 28, true, 1.5m));
// then r == 1234 / 9999;
Rational<long>.FromDecimal(0.123412m, out r, 28, true, 1.6m));
// then r == 123412 / 1000000; because of minimu repeating of period is 0.1234123 in this case.
Rounding at the end:
Rational<long>.FromDecimal(0.8888888888888888888888888889m, out r));
// then r == 8 == 9;
The most interesting case:
Rational<long>.FromDecimal(0.12345678m, out r, 28, true, 2, 9);
// then r == 12345678 / 100000000;
Rational<long>.FromDecimal(0.12345678m, out r, 28, true, 2, 8);
// Conversation failed, because of period has not been founded and there are too many digits in fraction part of input value.
Rational<long>.FromDecimal(0.12121212121212121m, out r, 28, true, 2, 9));
// then r == 4 / 33; Despite of too many digits in input value, period has been founded. Thus it's possible to convert value to fraction.
Other tests and code everyone can find in my MathFunctions library on github.
Ruby already has a built in solution:
0.33.rationalize.to_s # => "33/100"
0.4.rationalize.to_s # => "2/5"
In Rails, ActiveRecord numerical attributes can be converted too:
product.size = 0.33
product.size.to_r.to_s # => "33/100"
Answer in C++, assuming that you have a BigInt class, which can store unlimited-size integers.
You can use unsigned long long instead, but it will only work for certain values.
void GetRational(double val)
{
if (val == val+1) // Inf
throw "Infinite Value";
if (val != val) // NaN
throw "Undefined Value";
bool sign = false;
BigInt enumerator = 0;
BigInt denominator = 1;
if (val < 0)
{
val = -val;
sign = true;
}
while (val > 0)
{
unsigned int intVal = (unsigned int)val;
val -= intVal;
enumerator += intVal;
val *= 2;
enumerator *= 2;
denominator *= 2;
}
BigInt gcd = GCD(enumerator,denominator);
enumerator /= gcd;
denominator /= gcd;
Print(sign? "-":"+");
Print(enumerator);
Print("/");
Print(denominator);
// Or simply return {sign,enumerator,denominator} as you wish
}
BTW, GetRational(0.0) will return "+0/1", so you might wanna handle this case separately.
P.S.: I've been using this code in my own 'RationalNum' class for several years, and it's been tested thoroughly.
I think the best way to do this is to first convert your float value to an ascii representation. In C++ you could use ostringstream or in C, you could use sprintf. Here's how it would look in C++:
ostringstream oss;
float num;
cin >> num;
oss << num;
string numStr = oss.str();
int i = numStr.length(), pow_ten = 0;
while (i > 0) {
if (numStr[i] == '.')
break;
pow_ten++;
i--;
}
for (int j = 1; j < pow_ten; j++) {
num *= 10.0;
}
cout << static_cast<int>(num) << "/" << pow(10, pow_ten - 1) << endl;
A similar approach could be taken in straight C.
Afterwards you would need to check that the fraction is in lowest terms. This algorithm will give a precise answer, i.e. 0.33 would output "33/100", not "1/3." However, 0.4 would give "4/10," which when reduced to lowest terms would be "2/5." This may not be as powerful as EppStein's solution, but I believe this is more straightforward.
You'll have to figure out what level of error you're willing to accept. Not all decimal fractions will reduce to a simple fraction. I'd probably pick an easily-divisible number, like 60, and figure out how many 60ths is closest to the value, then simplify the fraction.
One solution is to just store all numbers as rational numbers in the first place. There are libraries for rational number arithmetic (eg GMP). If using an OO language you may be able to just use a rational number class library to replace your number class.
Finance programs, among others, would use such a solution to be able to make exact calculations and preserve precision that may be lost using a plain float.
Of course it will be a lot slower so it may not be practical for you. Depends on how much calculations you need to do, and how important the precision is for you.
a = rational(1);
b = rational(3);
c = a / b;
print (c.asFraction) ---> "1/3"
print (c.asFloat) ----> "0.333333"
Completed the above code and converted it to as3
public static function toFrac(f:Number) : String
{
if (f>1)
{
var parte1:int;
var parte2:Number;
var resultado:String;
var loc:int = String(f).indexOf(".");
parte2 = Number(String(f).slice(loc, String(f).length));
parte1 = int(String(f).slice(0,loc));
resultado = toFrac(parte2);
parte1 *= int(resultado.slice(resultado.indexOf("/") + 1, resultado.length)) + int(resultado.slice(0, resultado.indexOf("/")));
resultado = String(parte1) + resultado.slice(resultado.indexOf("/"), resultado.length)
return resultado;
}
if( f < 0.47 )
if( f < 0.25 )
if( f < 0.16 )
if( f < 0.13 )
if( f < 0.11 )
return "1/10";
else
return "1/9";
else
if( f < 0.14 )
return "1/8";
else
return "1/7";
else
if( f < 0.19 )
return "1/6";
else
if( f < 0.22 )
return "1/5";
else
return "2/9";
else
if( f < 0.38 )
if( f < 0.29 )
return "1/4";
else
if( f < 0.31 )
return "2/7";
else
return "1/3";
else
if( f < 0.43 )
if( f < 0.40 )
return "3/8";
else
return "2/5";
else
if( f < 0.44 )
return "3/7";
else
return "4/9";
else
if( f < 0.71 )
if( f < 0.60 )
if( f < 0.56 )
return "1/2";
else
if( f < 0.57 )
return "5/9";
else
return "4/7";
else
if( f < 0.63 )
return "3/5";
else
if( f < 0.66 )
return "5/8";
else
return "2/3";
else
if( f < 0.80 )
if( f < 0.74 )
return "5/7";
else
if(f < 0.78 )
return "3/4";
else
return "7/9";
else
if( f < 0.86 )
if( f < 0.83 )
return "4/5";
else
return "5/6";
else
if( f < 0.88 )
return "6/7";
else
if( f < 0.89 )
return "7/8";
else
if( f < 0.90 )
return "8/9";
else
return "9/10";
}
Here is a quick and dirty implementation in javascript that uses a brute force approach. Not at all optimized, it works within a predefined range of fractions: http://jsfiddle.net/PdL23/1/
/* This should convert any decimals to a simplified fraction within the range specified by the two for loops. Haven't done any thorough testing, but it seems to work fine.
I have set the bounds for numerator and denominator to 20, 20... but you can increase this if you want in the two for loops.
Disclaimer: Its not at all optimized. (Feel free to create an improved version.)
*/
decimalToSimplifiedFraction = function(n) {
for(num = 1; num < 20; num++) { // "num" is the potential numerator
for(den = 1; den < 20; den++) { // "den" is the potential denominator
var multiplyByInverse = (n * den ) / num;
var roundingError = Math.round(multiplyByInverse) - multiplyByInverse;
// Checking if we have found the inverse of the number,
if((Math.round(multiplyByInverse) == 1) && (Math.abs(roundingError) < 0.01)) {
return num + "/" + den;
}
}
}
};
//Put in your test number here.
var floatNumber = 2.56;
alert(floatNumber + " = " + decimalToSimplifiedFraction(floatNumber));This is inspired by the approach used by JPS.
You are going to have two basic problems that will make this hard:
1) Floating point isn't an exact representation which means that if you have a fraction of "x/y" which results in a value of "z", your fraction algorithm may return a result other than "x/y".
2) There are infinity many more irrational numbers than rational. A rational number is one that can be represented as a fraction. Irrational being ones that can not.
However, in a cheap sort of way, since floating point has limit accuracy, then you can always represent it as some form of faction. (I think...)
Here is implementation for ruby http://github.com/valodzka/frac
Math.frac(0.2, 100) # => (1/5)
Math.frac(0.33, 10) # => (1/3)
Math.frac(0.33, 100) # => (33/100)
I came across an especially elegant Haskell solution making use of an anamorphism. It depends on the recursion-schemes package.
{-# LANGUAGE AllowAmbiguousTypes #-}
{-# LANGUAGE FlexibleContexts #-}
import Control.Applicative (liftA2)
import Control.Monad (ap)
import Data.Functor.Foldable
import Data.Ratio (Ratio, (%))
isInteger :: (RealFrac a) => a -> Bool
isInteger = ((==) <*>) (realToFrac . floor)
continuedFraction :: (RealFrac a) => a -> [Int]
continuedFraction = liftA2 (:) floor (ana coalgebra)
where coalgebra x
| isInteger x = Nil
| otherwise = Cons (floor alpha) alpha
where alpha = 1 / (x - realToFrac (floor x))
collapseFraction :: (Integral a) => [Int] -> Ratio a
collapseFraction [x] = fromIntegral x % 1
collapseFraction (x:xs) = (fromIntegral x % 1) + 1 / collapseFraction xs
-- | Use the nth convergent to approximate x
approximate :: (RealFrac a, Integral b) => a -> Int -> Ratio b
approximate x n = collapseFraction $ take n (continuedFraction x)
If you try this out in ghci, it really does work!
λ:> approximate pi 2
22 % 7
As many people have stated you really can't convert a floating point back to a fraction (unless its extremely exact like .25). Of course you could create some type of look up for a large array of fractions and use some sort of fuzzy logic to produce the result you are looking for. Again this wouldn't be exact though and you would need to define a lower bounds of how large your want the denominator to go.
.32 < x < .34 = 1/3 or something like that.
