A cylinder impostor can actually be done just the same way as a sphere, like Nicol Bolas did it in his tutorial. You can make a square facing the camera and colour it that it will look like a cylinder, just the same way as Nicol did it for spheres. And it's not that hard.
The way it is done is ray-tracing of course. Notice that a cylinder facing upwards in camera space is kinda easy to implement. For example intersection with the side can be projected to the xz plain, it's a 2D problem of a line intersecting with a circle. Getting the top and bottom isn't harder either, the z coordinate of the intersection is given, so you actually know the intersection point of the ray and the circle's plain, all you have to do is to check if its inside the circle. And basically, that's it, you get two points, and return the closer one (the normals are pretty trivial too).
And when it comes to an arbitrary axis, it turns out to be almost the same problem. When you solve equations at the fixed axis cylinder, you are solving them for a parameter that describes how long do you have to go from a given point in a given direction to reach the cylinder. From the "definition" of it, you should notice that this parameter doesn't change if you rotate the world. So you can rotate the arbitrary axis to become the y axis, solve the problem in a space where equations are easier, get the parameter for the line equation in that space, but return the result in camera space.
You can download the shaderfiles from here. Just an image of it in action:
The code where the magic happens (It's only long 'cos it's full of comments, but the code itself is max 50 lines):
void CylinderImpostor(out vec3 cameraPos, out vec3 cameraNormal)
{
// First get the camera space direction of the ray.
vec3 cameraPlanePos = vec3(mapping * max(cylRadius, cylHeight), 0.0) + cameraCylCenter;
vec3 cameraRayDirection = normalize(cameraPlanePos);
// Now transform data into Cylinder space wherethe cyl's symetry axis is up.
vec3 cylCenter = cameraToCylinder * cameraCylCenter;
vec3 rayDirection = normalize(cameraToCylinder * cameraPlanePos);
// We will have to return the one from the intersection of the ray and circles,
// and the ray and the side, that is closer to the camera. For that, we need to
// store the results of the computations.
vec3 circlePos, sidePos;
vec3 circleNormal, sideNormal;
bool circleIntersection = false, sideIntersection = false;
// First check if the ray intersects with the top or bottom circle
// Note that if the ray is parallel with the circles then we
// definitely won't get any intersection (but we would divide with 0).
if(rayDirection.y != 0.0){
// What we know here is that the distance of the point's y coord
// and the cylCenter is cylHeight, and the distance from the
// y axis is less than cylRadius. So we have to find a point
// which is on the line, and match these conditions.
// The equation for the y axis distances:
// rayDirection.y * t - cylCenter.y = +- cylHeight
// So t = (+-cylHeight + cylCenter.y) / rayDirection.y
// About selecting the one we need:
// - Both has to be positive, or no intersection is visible.
// - If both are positive, we need the smaller one.
float topT = (+cylHeight + cylCenter.y) / rayDirection.y;
float bottomT = (-cylHeight + cylCenter.y) / rayDirection.y;
if(topT > 0.0 && bottomT > 0.0){
float t = min(topT,bottomT);
// Now check for the x and z axis:
// If the intersection is inside the circle (so the distance on the xz plain of the point,
// and the center of circle is less than the radius), then its a point of the cylinder.
// But we can't yet return because we might get a point from the the cylinder side
// intersection that is closer to the camera.
vec3 intersection = rayDirection * t;
if( length(intersection.xz - cylCenter.xz) <= cylRadius ) {
// The value we will (optianally) return is in camera space.
circlePos = cameraRayDirection * t;
// This one is ugly, but i didn't have better idea.
circleNormal = length(circlePos - cameraCylCenter) <
length((circlePos - cameraCylCenter) + cylAxis) ? cylAxis : -cylAxis;
circleIntersection = true;
}
}
}
// Find the intersection of the ray and the cylinder's side
// The distance of the point and the y axis is sqrt(x^2 + z^2), which has to be equal to cylradius
// (rayDirection.x*t - cylCenter.x)^2 + (rayDirection.z*t - cylCenter.z)^2 = cylRadius^2
// So its a quadratic for t (A*t^2 + B*t + C = 0) where:
// A = rayDirection.x^2 + rayDirection.z^2 - if this is 0, we won't get any intersection
// B = -2*rayDirection.x*cylCenter.x - 2*rayDirection.z*cylCenter.z
// C = cylCenter.x^2 + cylCenter.z^2 - cylRadius^2
// It will give two results, we need the smaller one
float A = rayDirection.x*rayDirection.x + rayDirection.z*rayDirection.z;
if(A != 0.0) {
float B = -2*(rayDirection.x*cylCenter.x + rayDirection.z*cylCenter.z);
float C = cylCenter.x*cylCenter.x + cylCenter.z*cylCenter.z - cylRadius*cylRadius;
float det = (B * B) - (4 * A * C);
if(det >= 0.0){
float sqrtDet = sqrt(det);
float posT = (-B + sqrtDet)/(2*A);
float negT = (-B - sqrtDet)/(2*A);
float IntersectionT = min(posT, negT);
vec3 Intersect = rayDirection * IntersectionT;
if(abs(Intersect.y - cylCenter.y) < cylHeight){
// Again it's in camera space
sidePos = cameraRayDirection * IntersectionT;
sideNormal = normalize(sidePos - cameraCylCenter);
sideIntersection = true;
}
}
}
// Now get the results together:
if(sideIntersection && circleIntersection){
bool circle = length(circlePos) < length(sidePos);
cameraPos = circle ? circlePos : sidePos;
cameraNormal = circle ? circleNormal : sideNormal;
} else if(sideIntersection){
cameraPos = sidePos;
cameraNormal = sideNormal;
} else if(circleIntersection){
cameraPos = circlePos;
cameraNormal = circleNormal;
} else
discard;
}
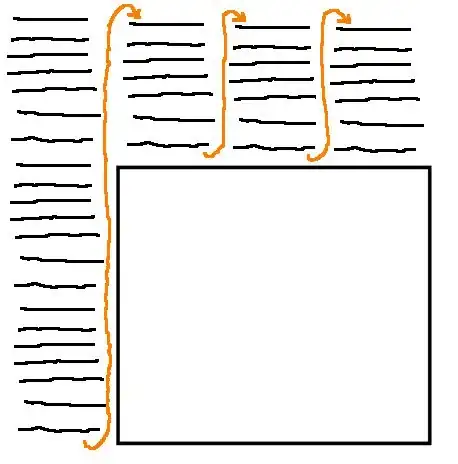Viewing angles. I have only taken the 0-90 case into account in the math below, but the other cases are trivially different.
Given the viewing angle (phi) and the diameter of the cylinder (a) here's how the shader needs to warp the Y-Axis in texture space Y = b' sin(phi). And b' = a * (phi / 90). The cases phi = 0 and phi = 90 should never be rendered.
