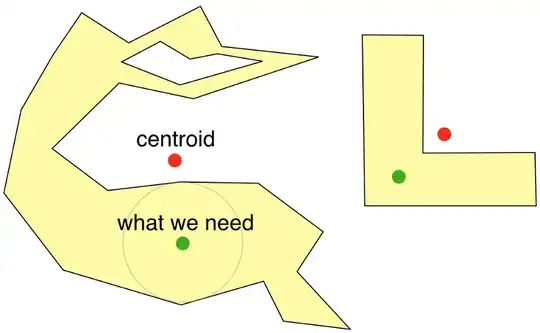
How can you find the centroid of a concave irregular polygon in JavaScript?

Question

How can you find the centroid of a concave irregular polygon given its vertices in JavaScript?

I want to pass a set of x,y points to a JavaScript function and be given an x,y point.

var my_points = [{x:3,y:1},{x:5,y:8},{x:2,y:9}];

function get_polygon_centroid(points){
    // answer
}

var my_centroid = get_polygon_centroid(my_points);

The my_points variable is only supposed to represent the format of the points to be given, not to represent the specific count of points to be given.

The centroid returned will be a point somewhere inside the polygon.

The end goal would be to add a marker at the centroid of a polygon in a Google Maps V3 application.

Answer 1

For the centroid of the 2D surface (which is likely to be what you need), The best is to start with a little bit of maths.

I adapted it here to your own notation :

function get_polygon_centroid(pts) {
   var first = pts[0], last = pts[pts.length-1];
   if (first.x != last.x || first.y != last.y) pts.push(first);
   var twicearea=0,
   x=0, y=0,
   nPts = pts.length,
   p1, p2, f;
   for ( var i=0, j=nPts-1 ; i<nPts ; j=i++ ) {
      p1 = pts[i]; p2 = pts[j];
      f = p1.x*p2.y - p2.x*p1.y;
      twicearea += f;          
      x += ( p1.x + p2.x ) * f;
      y += ( p1.y + p2.y ) * f;
   }
   f = twicearea * 3;
   return { x:x/f, y:y/f };
}

Answer 2

The accepted answer has an issue which becomes prominent as the polygon's area becomes smaller. It would not be visible in most cases, but can result in some weird results at very small dimensions. Here's an update to that solution to account for this issue.

function get_polygon_centroid(pts) {
   var first = pts[0], last = pts[pts.length-1];
   if (first.x != last.x || first.y != last.y) pts.push(first);
   var twicearea=0,
   x=0, y=0,
   nPts = pts.length,
   p1, p2, f;
   for ( var i=0, j=nPts-1 ; i<nPts ; j=i++ ) {
      p1 = pts[i]; p2 = pts[j];
      f = (p1.y - first.y) * (p2.x - first.x) - (p2.y - first.y) * (p1.x - first.x);
      twicearea += f;
      x += (p1.x + p2.x - 2 * first.x) * f;
      y += (p1.y + p2.y - 2 * first.y) * f;
   }
   f = twicearea * 3;
   return { x:x/f + first.x, y:y/f + first.y };
}

Here's a case of a centroid ending up outside of a small polygon for anyone curious as to what I'm talking about:

var points = [
    {x:78.0001462, y: 40.0008827},
    {x:78.0000228, y: 40.0008940},
    {x:78.0000242, y: 40.0009264},
    {x:78.0001462, y: 40.0008827},
];
// original get_polygon_centroid(points)
// results in { x: 77.99957948181007, y: 40.00065236005001 }
console.log(get_polygon_centroid(points))
// result is { x: 78.0000644, y: 40.000901033333335 }

Answer 3

If you want the label to be positioned within the concave irregular polygon, then the above answers do not work very well. The centroid of a concave polygon could be very likely outside the polygon.

There's this Polylabel library that addresses the problem very well. This blog article gives the details of the algorithm. If you want to use the library in browser and don't want to package it yourself, you can download the library from this page.

Code example to use the library:

function get_polygon_centroid(points) {
    var pts = points.map(p => [p.x, p.y]);  // convert {x:x, y:y} into [x, y]
    var centroid = polylabel([pts]);
    return {x:centroid[0], y:centroid[1]};
}
var my_points = [{x:3,y:1},{x:5,y:8},{x:2,y:9}];
console.log('centroid', get_polygon_centroid(my_points));

Answer 4

This is fairly simple to do. The centroid of a finite set of k points x₁, x₂, ... x_k is described by the formula

(x₁ + x₂ + ... + x_k) / k

That means we can just add all the points up and then divide by the number of points, like this:

function getPolygonCentroid(points){ 
  var centroid = {x: 0, y: 0};
  for(var i = 0; i < points.length; i++) {
     var point = points[i];
     centroid.x += point.x;
     centroid.y += point.y;
  }
  centroid.x /= points.length;
  centroid.y /= points.length;
  return centroid;
} 

Answer 5

If you are not casual about the definition of 'centroid', this is the formula for the centroid of a polygon. As you can see, it's sufficiently more complicated than the centroid of a set of points. If you can do with the centroid of the points, that's fine, but if you want the centroid of the polygon, you'd have to implement this formula, which btw is not very difficult. Please remember that in the general case of an irregular polygon, which is your case, these two centroids will be different (otherwise this formula wouldn't exist).

Answer 6

Building on Myobis' and pragmar's answers, it's not necessary to alter the array by duplicating the first element. In fact, in their implementation the first iteration of the for loop doesn't do anything because pts[i] and pts[j] are identical.

Here is the same algorithm with some optimizations (originally ported from Finding the centroid of a polygon?):

function get_polygon_centroid(points) {
    //Correction for very small polygons:
    const x0 = points[0].x , y0 = points[0].y;

    let x = 0, y = 0, twiceArea = 0;

    let prev = points[points.length - 1];
    for (const next of points)
    {
        const x1 = prev.x - x0, y1 = prev.y - y0,
              x2 = next.x - x0, y2 = next.y - y0,
              a  = x1 * y2 - x2 * y1;

        twiceArea += a;
        x += (x1 + x2) * a;
        y += (y1 + y2) * a;

        prev = next;
    }

    const factor = 3 * twiceArea;  // 6 * twiceArea/2
    x /= factor;
    y /= factor;

    return { x: x + x0, y: y + y0 };
}

const points = [
    { x: 78.0001462, y: 40.0008827 },
    { x: 78.0000228, y: 40.0008940 },
    { x: 78.0000242, y: 40.0009264 },
];
console.log(get_polygon_centroid(points));