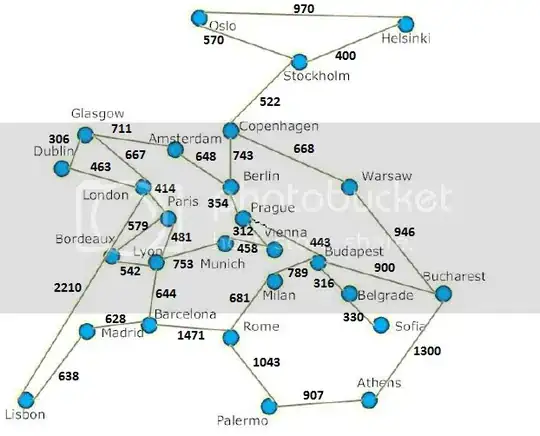
I have to make an uninformed search (Breadth-first-Search) program which takes two nodes and return all the paths between them.
public void BFS(Nod start, Nod end) {
Queue<Nod> queue = new Queue<Nod>();
queue.Enqueue(start);
while (queue.Count != 0)
{
Nod u = queue.Dequeue();
if (u == end) break;
else
{
u.data = "Visited";
foreach (Edge edge in u.getChildren())
{
if (edge.getEnd().data == "")
{
edge.getEnd().data = "Visited";
if (edge.getEnd() != end)
{
edge.getEnd().setParent(u);
}
else
{
edge.getEnd().setParent(u);
cost = 0;
PrintPath(edge.getEnd(), true);
edge.getEnd().data = "";
//return;
}
}
queue.Enqueue(edge.getEnd());
}
}
}
}
My problem is that i only get two paths instead of all and i don't know what to edit in my code to get them all. The input of my problem is based on this map :