Double subtraction precision issue

Question

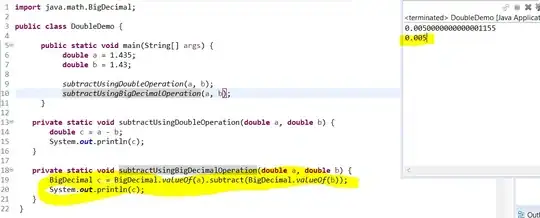
My coworker did this experiment:

public class DoubleDemo {

      public static void main(String[] args) {
           double a = 1.435;
           double b = 1.43;
           double c = a - b;
           System.out.println(c);
      }
 }

For this first-grade operation I expected this output:

0.005

But unexpectedly the output was:

0.0050000000000001155

Why does double fails in such a simple operation? And if double is not the datatype for this work, what should I use?

Answer 1

double is internally stored as a fraction in binary -- like 1/4 + 1/8 + 1/16 + ...

The value 0.005 -- or the value 1.435 -- cannot be stored as an exact fraction in binary, so double cannot store the exact value 0.005, and the subtracted value isn't quite exact.

If you care about precise decimal arithmetic, use BigDecimal.

You may also find this article useful reading.

Answer 2

double and float are not exactly real numbers.

There are infinite number of real numbers in any range, but only finite number of bits to represent them! for this reason, rounding errors is expected for double and floats.

The number you get is the closest number possible that can be represented by double in floating point representation.

For more details, you might want to read this article [warning: might be high-level].

You might want to use BigDecimal to get exactly a decimal number [but you will again encounter rounding errors when you try to get 1/3].

Answer 3

Yes it worked this way using BigDecimal operations

private static void subtractUsingBigDecimalOperation(double a, double b) {
  BigDecimal c = BigDecimal.valueOf(a).subtract(BigDecimal.valueOf(b));
  System.out.println(c);
}

Answer 4

double and float arithmetic are never going to be exactly correct because of the rounding that occurs "under the hood".

Essentially doubles and floats can have an infinite amount of decimals but in memory they must be represented by some real number of bits. So when you do this decimal arithmetic a rounding procedure occurs and is often off by a very small amount if you take all of the decimals into account.

As suggested earlier, if you need completely exact values then use BigDecimal which stores its values differently. Here's the API

Answer 5

public class BigDecimalExample {

    public static void main(String args[]) throws IOException {

      //floating point calculation
      double amount1 = 2.15;
      double amount2 = 1.10;
      System.out.println("difference between 2.15 and 1.0 using double is: " + (amount1 - amount2));

      //Use BigDecimal for financial calculation
      BigDecimal amount3 = new BigDecimal("2.15");
      BigDecimal amount4 = new BigDecimal("1.10") ;
      System.out.println("difference between 2.15 and 1.0 using BigDecimal is: " + (amount3.subtract(amount4)));       
    }      
}

Output:

difference between 2.15 and 1.0 using double is: 1.0499999999999998 difference between 2.15 and 1.0 using BigDecmial is: 1.05

Answer 6

 //just try to make a quick example to make b to have the same precision as a has, by using BigDecimal

 private double getDesiredPrecision(Double a, Double b){
     String[] splitter = a.toString().split("\\.");
     splitter[0].length();   // Before Decimal Count
     int numDecimals = splitter[1].length(); //After Decimal Count

     BigDecimal bBigDecimal = new BigDecimal(b);
     bBigDecimal = bBigDecimal.setScale(numDecimals,BigDecimal.ROUND_HALF_EVEN);

     return bBigDecimal.doubleValue();  
 }