All the FFT implementations we have come across result in complex values (with real and imaginary parts), even if the input to the algorithm was a discrete set of real numbers (integers).
Is it not possible to represent frequency domain in terms of real numbers only?
The FFT is fundamentally a change of basis. The basis into which the FFT changes your original signal is a set of sine waves instead. In order for that basis to describe all the possible inputs it needs to be able to represent phase as well as amplitude; the phase is represented using complex numbers.
For example, suppose you FFT a signal containing only a single sine wave. Depending on phase you might well get an entirely real FFT result. But if you shift the phase of your input a few degrees, how else can the FFT output represent that input?
edit: This is a somewhat loose explanation, but I'm just trying to motivate the intuition.
The FFT provides you with amplitude and phase. The amplitude is encoded as the magnitude of the complex number (sqrt(x^2+y^2)) while the phase is encoded as the angle (atan2(y,x)). To have a strictly real result from the FFT, the incoming signal must have even symmetry (i.e. x[n]=conj(x[N-n])).
If all you care about is intensity, the magnitude of the complex number is sufficient for analysis.
Yes, it is possible to represent the FFT frequency domain results of strictly real input using only real numbers.
Those complex numbers in the FFT result are simply just 2 real numbers, which are both required to give you the 2D coordinates of a result vector that has both a length and a direction angle (or magnitude and a phase). And every frequency component in the FFT result can have a unique amplitude and a unique phase (relative to some point in the FFT aperture).
One real number alone can't represent both magnitude and phase. If you throw away the phase information, that could easily massively distort the signal if you try to recreate it using an iFFT (and the signal isn't symmetric). So a complete FFT result requires 2 real numbers per FFT bin. These 2 real numbers are bundled together in some FFTs in a complex data type by common convention, but the FFT result could easily (and some FFTs do) just produce 2 real vectors (one for cosine coordinates and one for sine coordinates).
There are also FFT routines that produce magnitude and phase directly, but they run more slowly than FFTs that produces a complex (or two real) vector result. There also exist FFT routines that compute only the magnitude and just throw away the phase information, but they usually run no faster than letting you do that yourself after a more general FFT. Maybe they save a coder a few lines of code at the cost of not being invertible. But a lot of libraries don't bother to include these slower and less general forms of FFT, and just let the coder convert or ignore what they need or don't need.
Plus, many consider the math involved to be a lot more elegant using complex arithmetic (where, for strictly real input, the cosine correlation or even component of an FFT result is put in the real component, and the sine correlation or odd component of the FFT result is put in the imaginary component of a complex number.)
(Added:) And, as yet another option, you can consider the two components of each FFT result bin, instead of as real and imaginary components, as even and odd components, both real.
If your FFT coefficient for a given frequency f is x + i y, you can look at x as the coefficient of a cosine at that frequency, while the y is the coefficient of the sine. If you add these two waves for a particular frequency, you will get a phase-shifted wave at that frequency; the magnitude of this wave is sqrt(x*x + y*y), equal to the magnitude of the complex coefficient.
The Discrete Cosine Transform (DCT) is a relative of the Fourier transform which yields all real coefficients. A two-dimensional DCT is used by many image/video compression algorithms.
The discrete Fourier transform is fundamentally a transformation from a vector of complex numbers in the "time domain" to a vector of complex numbers in the "frequency domain" (I use quotes because if you apply the right scaling factors, the DFT is its own inverse). If your inputs are real, then you can perform two DFTs at once: Take the input vectors x and y and calculate F(x + i y). I forget how you separate the DFT afterwards, but I suspect it's something about symmetry and complex conjugates.
The discrete cosine transform sort-of lets you represent the "frequency domain" with the reals, and is common in lossy compression algorithms (JPEG, MP3). The surprising thing (to me) is that it works even though it appears to discard phase information, but this also seems to make it less useful for most signal processing purposes (I'm not aware of an easy way to do convolution/correlation with a DCT).
I've probably gotten some details wrong ;)
The way you've phrased this question, I believe you are looking for a more intuitive way of thinking rather than a mathematical answer. I come from a mechanical engineering background and this is how I think about the Fourier transform. I contextualize the Fourier transform with reference to a pendulum. If we have only the x-velocity vs time of a pendulum and we are asked to estimate the energy of the pendulum (or the forcing source of the pendulum), the Fourier transform gives a complete answer. As usually what we are observing is only the x-velocity, we might conclude that the pendulum only needs to be provided energy equivalent to its sinusoidal variation of kinetic energy. But the pendulum also has potential energy. This energy is 90 degrees out of phase with the potential energy. So to keep track of the potential energy, we are simply keeping track of the 90 degree out of phase part of the (kinetic)real component. The imaginary part may be thought of as a 'potential velocity' that represents a manifestation of the potential energy that the source must provide to force the oscillatory behaviour. What is helpful is that this can be easily extended to the electrical context where capacitors and inductors also store the energy in 'potential form'. If the signal is not sinusoidal of course the transform is trying to decompose it into sinusoids. This I see as assuming that the final signal was generated by combined action of infinite sources each with a distinct sinusoid behaviour. What we are trying to determine is a strength and phase of each source that creates the final observed signal at each time instant.
PS: 1) The last two statements is generally how I think of the Fourier transform itself. 2) I say potential velocity rather the potential energy as the transform usually does not change dimensions of the original signal or physical quantity so it cannot shift from representing velocity to energy.
Short answer
Why does FFT produce complex numbers instead of real numbers?
The reason FT result is a complex array is a complex exponential multiplier is involved in the coefficients calculation. The final result is therefore complex. FT uses the multiplier to correlate the signal against multiple frequencies. The principle is detailed further down.
Is it not possible to represent frequency domain in terms of real numbers only?
Of course the 1D array of complex coefficients returned by FT could be represented by a 2D array of real values, which can be either the Cartesian coordinates x and y, or the polar coordinates r and θ (more here). However...
Complex exponential form is the most suitable form for signal processing
Having only real data is not so useful.
On one hand it is already possible to get these coordinates using one of the functions real, imag, abs and angle.
On the other hand such isolated information is of very limited interest. E.g. if we add two signals with the same amplitude and frequency, but in phase opposition, the result is zero. But if we discard the phase information, we just double the signal, which is totally wrong.
Contrary to a common belief, the use of complex numbers is not because such a number is a handy container which can hold two independent values. It's because processing periodic signals involves trigonometry all the time, and there is a simple way to move from sines and cosines to more simple complex numbers algebra: Euler's formula.
So most of the time signals are just converted to their complex exponential form. E.g. a signal with frequency 10 Hz, amplitude 3 and phase π/4 radians:
can be described by x = 3.ei(2π.10.t+π/4).
splitting the exponent: x = 3.ei.π/4 times ei.2π.10.t, t being the time.
The first number is a constant called the phasor. A common compact form is 3∠π/4. The second number is a time-dependent variable called the carrier.
This signal 3.ei.π/4 times ei.2π.10.t is easily plotted, either as a cosine (real part) or a sine (imaginary part):
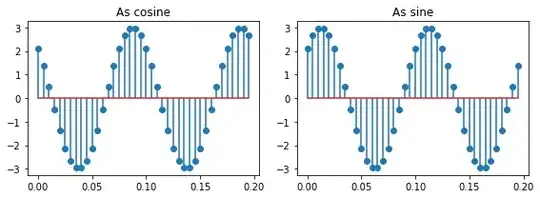
from numpy import arange, pi, e, real, imag
t = arange(0, 0.2, 1/200)
x = 3 * e ** (1j*pi/4) * e ** (1j*2*pi*10*t)
ax1.stem(t, real(x))
ax2.stem(t, imag(x))
Now if we look at FT coefficients, we see they are phasors, they don't embed the frequency which is only dependent on the number of samples and the sampling frequency.
Actually if we want to plot a FT component in the time domain, we have to separately create the carrier from the frequency found, e.g. by calling fftfreq. With the phasor and the carrier we have the spectral component.
A phasor is a vector, and a vector can turn
Cartesian coordinates are extracted by using real and imag functions, the phasor used above, 3.e(i.π/4), is also the complex number 2.12 + 2.12j (i is j for scientists and engineers). These coordinates can be plotted on a plane with the vertical axis representing i (left):
This point can also represent a vector (center). Polar coordinates can be used in place of Cartesian coordinates (right). Polar coordinates are extracted by abs and angle. It's clear this vector can also represent the phasor 3∠π/4 (short form for 3.e(i.π/4))
This reminder about vectors is to introduce how phasors are manipulated. Say we have a real number of amplitude 1, which is not less than a complex which angle is 0 and also a phasor (x∠0). We also have a second phasor (3∠π/4), and we want the product of the two phasors. We could compute the result using Cartesian coordinates with some trigonometry, but this is painful. The easiest way is to use the complex exponential form:
we just add the angles and multiply the real coefficients: 1.e(i.0) times 3.e(i.π/4) = 1x3.ei(0+π/4) = 3.e(i.π/4)
we can just write: (1∠0) times (3∠π/4) = (3∠π/4).
Whatever, the result is this one:
The practical effect is to turn the real number and scale its magnitude. In FT, the real is the sample amplitude, and the multiplier magnitude is actually 1, so this corresponds to this operation, but the result is the same:
This long introduction was to explain the math behind FT.
How spectral coefficients are created by FT
FT principle is, for each spectral coefficient to compute:
to multiply each of the samples amplitudes by a different phasor, so that the angle is increasing from the first sample to the last,
to sum all the previous products.
If there are N samples xn (0 to N-1), there are N spectral coefficients Xk to compute. Calculation of coefficient Xk involves multiplying each sample amplitude xn by the phasor e-i2πkn/N and taking the sum, according to FT equation:
In the N individual products, the multiplier angle varies according to 2π.n/N and k, meaning the angle changes, ignoring k for now, from 0 to 2π. So while performing the products, we multiply a variable real amplitude by a phasor which magnitude is 1 and angle is going from 0 to a full round. We know this multiplication turns and scales the real amplitude:
Source: A. Dieckmann from Physikalisches Institut der Universität Bonn
Doing this summation is actually trying to correlate the signal samples to the phasor angular velocity, which is how fast its angle varies with n/N. The result tells how strong this correlation is (amplitude), and how much synchroneous it is (phase).
This operation is repeated for the k spectral coefficients to compute (half with k negative, half with k positive). As k changes, the angle increment also varies, so the correlation is checked against another frequency.
Conclusion
FT results are neither sines nor cosines, they are not waves, they are phasors describing a correlation. A phasor is a constant, expressed as a complex exponential, embedding both amplitude and phase. Multiplied by a carrier, which is also a complex exponential, but variable, dependent on time, they draw helices in time domain:
When these helices are projected onto the horizontal plane, this is done by taking the real part of the FT result, the function drawn is the cosine. When projected onto the vertical plane, which is done by taking the imaginary part of the FT result, the function drawn is the sine. The phase determines at which angle the helix starts and therefore without the phase, the signal cannot be reconstructed using an inverse FT.
The complex exponential multiplier is a tool to transform the linear velocity of amplitude variations into angular velocity, which is frequency times 2π. All that revolves around Euler's formula linking sinusoid and complex exponential.
For a signal with only cosine waves, fourier transform, aka. FFT produces completely real output. For a signal composed of only sine waves, it produces completely imaginary output. A phase shift in any of the signals will result in a mix of real and complex. Complex numbers (in this context) are merely another way to store phase and amplitude.
