R: Interaction Plot with a continuous and a categorical variable for a GLMM (lme4)

Question

I would like to make an interaction plot to visually display the difference or similarity in slopes of interaction of a categorical variable (4 levels) and a standardized continuous variable from the results of a regression model.

with(GLMModel, interaction.plot(continuous.var, categorical.var, response.var)) Is not what I am looking for. It produces a plot in which the slope changes for each value of the continuous variable. I'm looking to make a plot with constant slopes as in the following plot:

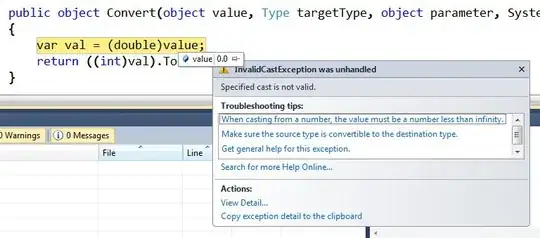
enter image description here

Any ideas?

I fit a model of the form fit<-glmer(resp.var ~ cont.var*cat.var + (1|rand.eff) , data = sample.data , poisson) Here is some sample data:

structure(list(cat.var = structure(c(4L, 4L, 1L, 4L, 1L, 2L, 
1L, 1L, 1L, 1L, 4L, 1L, 1L, 3L, 2L, 4L, 1L, 1L, 1L, 2L, 1L, 2L, 
2L, 1L, 3L, 1L, 1L, 2L, 4L, 1L, 2L, 1L, 1L, 4L, 1L, 3L, 1L, 3L, 
3L, 4L, 3L, 4L, 1L, 3L, 3L, 1L, 2L, 3L, 4L, 3L, 4L, 2L, 1L, 1L, 
4L, 1L, 1L, 1L, 1L, 1L, 1L, 4L, 1L, 4L, 4L, 3L, 3L, 1L, 3L, 3L, 
3L, 1L, 2L, 1L, 1L, 1L, 1L, 2L, 2L, 4L, 1L, 3L, 4L, 1L, 1L, 4L, 
1L, 3L, 1L, 1L, 3L, 2L, 4L, 1L, 4L, 1L, 4L, 4L, 4L, 4L, 2L, 4L, 
4L, 1L, 2L, 1L, 4L, 3L, 1L, 1L, 3L, 2L, 4L, 4L, 1L, 4L, 1L, 3L, 
2L, 1L, 2L, 1L, 2L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 2L, 4L, 1L, 
2L, 2L, 1L, 1L, 2L, 3L, 1L, 4L, 4L, 4L, 1L, 4L, 4L, 3L, 2L, 4L, 
1L, 3L, 1L, 1L, 4L, 4L, 2L, 4L, 1L, 1L, 3L, 4L, 2L, 1L, 3L, 3L, 
4L, 3L, 2L, 3L, 1L, 4L, 2L, 2L, 1L, 4L, 1L, 2L, 3L, 4L, 1L, 4L, 
2L, 1L, 3L, 3L, 3L, 4L, 1L, 1L, 1L, 3L, 1L, 3L, 4L, 2L, 1L, 4L, 
1L, 1L, 1L, 2L, 1L, 1L, 4L, 1L, 3L, 1L, 2L, 1L, 4L, 1L, 2L, 4L, 
1L, 1L, 1L, 2L, 1L, 1L, 1L, 1L, 1L, 3L, 1L, 3L, 4L, 1L, 4L, 3L, 
3L, 3L, 4L, 1L, 3L, 1L, 1L, 4L, 4L, 4L, 4L, 2L, 1L, 1L, 3L, 2L, 
1L, 4L, 4L, 2L, 4L, 2L, 4L, 1L, 3L, 4L, 1L, 1L, 2L, 3L, 2L, 4L, 
1L, 1L, 3L, 4L, 2L, 2L, 3L, 4L, 1L, 2L, 3L, 1L, 2L, 4L, 1L, 4L, 
2L, 4L, 3L, 4L, 2L, 1L, 1L, 1L, 1L, 1L, 4L, 4L, 1L, 4L, 4L, 1L, 
4L, 2L, 1L, 1L, 1L, 1L, 3L, 1L, 1L, 3L, 3L, 2L, 2L, 1L, 1L, 4L, 
1L, 4L, 3L, 1L, 2L, 1L, 4L, 2L, 4L, 4L, 1L, 2L, 1L, 1L, 1L, 4L, 
1L, 4L, 1L, 2L, 1L, 3L, 1L, 3L, 3L, 1L, 1L, 4L, 3L, 1L, 4L, 1L, 
2L, 4L, 1L, 1L, 3L, 3L, 2L, 4L, 4L, 1L, 1L, 2L, 2L, 1L, 2L, 4L, 
3L, 4L, 4L, 4L, 4L, 1L, 3L, 1L, 2L, 2L, 2L, 4L, 2L, 3L, 4L, 1L, 
3L, 2L, 2L, 1L, 1L, 1L, 3L, 1L, 2L, 2L, 1L, 1L, 3L, 2L, 1L, 1L, 
1L, 1L, 2L, 1L, 1L, 1L, 4L, 4L, 4L, 3L, 3L, 2L, 1L, 3L, 2L, 1L, 
1L, 1L, 4L, 1L, 1L, 2L, 3L, 1L, 1L, 2L, 4L, 3L, 2L, 4L, 3L, 2L, 
1L, 3L, 1L, 3L, 1L, 4L, 3L, 1L, 4L, 4L, 2L, 4L, 1L, 1L, 2L, 4L, 
4L, 2L, 3L, 4L, 4L, 3L, 1L, 4L, 1L, 2L, 4L, 1L, 1L, 4L, 1L, 1L, 
1L, 1L, 1L, 3L, 4L, 1L, 4L, 4L, 2L, 2L, 2L, 2L, 3L, 4L, 4L, 1L, 
1L, 4L, 2L, 3L, 3L, 1L, 1L, 1L, 1L, 3L, 1L, 1L, 1L, 3L, 4L, 2L, 
3L, 1L, 1L, 1L, 4L, 1L, 1L, 4L, 4L, 4L, 1L, 1L, 1L, 1L), .Label = c("A", 
"B", "C", "D"), class = "factor"), cont.var = c(-0.0682900527296927, 
0.546320421837542, -0.273160210918771, -0.887770685486005, 0.136580105459385, 
0.75119058002662, 0.546320421837542, -0.273160210918771, -0.682900527296927, 
0.136580105459385, 0.75119058002662, 0.75119058002662, 0.75119058002662, 
0.341450263648464, 0.75119058002662, 0.546320421837542, 0.546320421837542, 
-0.478030369107849, -0.478030369107849, -0.682900527296927, -0.682900527296927, 
0.546320421837542, -0.478030369107849, -0.0682900527296927, 0.136580105459385, 
0.136580105459385, 0.75119058002662, -0.478030369107849, 0.75119058002662, 
-0.887770685486005, 0.136580105459385, -0.478030369107849, 0.341450263648464, 
-0.682900527296927, -0.478030369107849, 0.341450263648464, -0.478030369107849, 
0.546320421837542, 0.75119058002662, -0.478030369107849, -0.273160210918771, 
0.546320421837542, -0.682900527296927, 0.75119058002662, -0.478030369107849, 
-0.887770685486005, 0.136580105459385, -0.887770685486005, -0.0682900527296927, 
-0.478030369107849, 0.546320421837542, 0.75119058002662, 0.136580105459385, 
-0.273160210918771, -0.273160210918771, 0.75119058002662, -0.682900527296927, 
0.136580105459385, -0.273160210918771, -0.273160210918771, 0.136580105459385, 
0.136580105459385, 0.341450263648464, 0.136580105459385, -0.273160210918771, 
-0.273160210918771, -0.682900527296927, -0.887770685486005, -0.0682900527296927, 
0.136580105459385, -0.0682900527296927, -0.273160210918771, -0.273160210918771, 
0.341450263648464, 0.75119058002662, -0.682900527296927, -0.0682900527296927, 
-0.273160210918771, -0.887770685486005, -0.0682900527296927, 
0.75119058002662, 0.546320421837542, 0.75119058002662, 0.75119058002662, 
-0.887770685486005, 0.341450263648464, 0.75119058002662, -0.887770685486005, 
0.136580105459385, -0.273160210918771, 0.546320421837542, 0.546320421837542, 
-0.682900527296927, 0.75119058002662, 0.136580105459385, -0.0682900527296927, 
-0.478030369107849, 0.75119058002662, -0.478030369107849, 0.341450263648464, 
0.136580105459385, -0.0682900527296927, -0.478030369107849, -0.0682900527296927, 
-0.0682900527296927, 0.546320421837542, -0.273160210918771, 0.75119058002662, 
0.341450263648464, 0.546320421837542, -0.478030369107849, 0.136580105459385, 
-0.887770685486005, -0.273160210918771, -0.273160210918771, -0.478030369107849, 
-0.478030369107849, 0.75119058002662, -0.682900527296927, -0.0682900527296927, 
0.546320421837542, 0.75119058002662, 0.546320421837542, 0.136580105459385, 
-0.478030369107849, 0.136580105459385, 0.546320421837542, -0.478030369107849, 
-0.0682900527296927, -0.0682900527296927, 0.546320421837542, 
-0.273160210918771, 0.136580105459385, -0.0682900527296927, 0.75119058002662, 
-0.0682900527296927, 0.546320421837542, -0.887770685486005, -0.0682900527296927, 
-0.682900527296927, -0.478030369107849, -0.478030369107849, -0.682900527296927, 
0.75119058002662, 0.341450263648464, -0.0682900527296927, 0.341450263648464, 
-0.0682900527296927, -0.887770685486005, -0.887770685486005, 
-0.273160210918771, -0.0682900527296927, 0.546320421837542, -0.0682900527296927, 
-0.0682900527296927, 0.75119058002662, -0.0682900527296927, -0.273160210918771, 
-0.478030369107849, 0.546320421837542, 0.546320421837542, 0.546320421837542, 
0.341450263648464, 0.136580105459385, -0.478030369107849, 0.136580105459385, 
0.136580105459385, 0.136580105459385, -0.478030369107849, -0.273160210918771, 
-0.273160210918771, -0.273160210918771, 0.341450263648464, -0.273160210918771, 
-0.0682900527296927, 0.136580105459385, 0.546320421837542, -0.478030369107849, 
-0.273160210918771, 0.546320421837542, 0.546320421837542, -0.273160210918771, 
-0.0682900527296927, 0.341450263648464, 0.546320421837542, -0.0682900527296927, 
0.136580105459385, -0.478030369107849, 0.75119058002662, -0.478030369107849, 
-0.682900527296927, -0.478030369107849, 0.136580105459385, -0.273160210918771, 
-0.0682900527296927, -0.887770685486005, -0.887770685486005, 
0.546320421837542, -0.273160210918771, 0.546320421837542, -0.478030369107849, 
0.546320421837542, -0.0682900527296927, 0.75119058002662, -0.273160210918771, 
0.546320421837542, 0.341450263648464, -0.0682900527296927, -0.0682900527296927, 
-0.0682900527296927, -0.887770685486005, 0.136580105459385, -0.273160210918771, 
-0.478030369107849, 0.75119058002662, 0.341450263648464, 0.546320421837542, 
-0.273160210918771, 0.546320421837542, 0.75119058002662, -0.273160210918771, 
0.75119058002662, 0.546320421837542, -0.273160210918771, -0.273160210918771, 
0.75119058002662, -0.273160210918771, -0.0682900527296927, 0.136580105459385, 
-0.478030369107849, 0.75119058002662, 0.75119058002662, -0.887770685486005, 
-0.887770685486005, 0.546320421837542, -0.682900527296927, -0.887770685486005, 
0.136580105459385, 0.75119058002662, 0.75119058002662, -0.478030369107849, 
0.136580105459385, 0.75119058002662, -0.273160210918771, -0.682900527296927, 
-0.273160210918771, 0.136580105459385, 0.546320421837542, -0.682900527296927, 
-0.478030369107849, 0.136580105459385, -0.682900527296927, -0.0682900527296927, 
-0.478030369107849, 0.136580105459385, -0.887770685486005, -0.273160210918771, 
-0.0682900527296927, -0.273160210918771, -0.887770685486005, 
0.546320421837542, 0.546320421837542, -0.478030369107849, -0.273160210918771, 
-0.0682900527296927, 0.136580105459385, -0.478030369107849, 0.75119058002662, 
0.341450263648464, 0.136580105459385, 0.136580105459385, 0.75119058002662, 
0.136580105459385, -0.0682900527296927, 0.546320421837542, -0.0682900527296927, 
-0.887770685486005, 0.75119058002662, 0.75119058002662, 0.546320421837542, 
-0.887770685486005, -0.0682900527296927, -0.682900527296927, 
-0.682900527296927, 0.75119058002662, 0.75119058002662, -0.478030369107849, 
0.546320421837542, -0.273160210918771, 0.75119058002662, -0.0682900527296927, 
0.546320421837542, -0.0682900527296927, -0.273160210918771, 0.546320421837542, 
0.75119058002662, -0.0682900527296927, 0.546320421837542, -0.682900527296927, 
-0.273160210918771, -0.0682900527296927, -0.478030369107849, 
-0.478030369107849, 0.136580105459385, -0.273160210918771, 0.136580105459385, 
0.546320421837542, 0.75119058002662, -0.273160210918771, 0.341450263648464, 
-0.273160210918771, 0.136580105459385, 0.546320421837542, 0.546320421837542, 
0.136580105459385, 0.136580105459385, -0.682900527296927, 0.341450263648464, 
0.341450263648464, -0.273160210918771, -0.682900527296927, -0.0682900527296927, 
0.75119058002662, -0.887770685486005, -0.478030369107849, -0.273160210918771, 
-0.478030369107849, -0.478030369107849, 0.136580105459385, -0.478030369107849, 
0.136580105459385, -0.478030369107849, 0.136580105459385, -0.0682900527296927, 
-0.273160210918771, 0.136580105459385, 0.341450263648464, -0.478030369107849, 
0.75119058002662, 0.136580105459385, 0.341450263648464, 0.546320421837542, 
-0.887770685486005, 0.75119058002662, 0.341450263648464, -0.0682900527296927, 
-0.478030369107849, 0.546320421837542, 0.136580105459385, -0.682900527296927, 
-0.0682900527296927, 0.341450263648464, -0.478030369107849, -0.0682900527296927, 
-0.478030369107849, -0.0682900527296927, 0.341450263648464, -0.478030369107849, 
-0.682900527296927, 0.75119058002662, -0.478030369107849, -0.682900527296927, 
0.341450263648464, -0.887770685486005, -0.478030369107849, 0.546320421837542, 
-0.887770685486005, -0.478030369107849, -0.478030369107849, 0.341450263648464, 
0.75119058002662, -0.682900527296927, 0.75119058002662, 0.75119058002662, 
0.341450263648464, -0.0682900527296927, 0.546320421837542, -0.0682900527296927, 
0.136580105459385, 0.136580105459385, 0.136580105459385, 0.136580105459385, 
0.546320421837542, 0.546320421837542, -0.0682900527296927, 0.75119058002662, 
-0.0682900527296927, -0.0682900527296927, -0.682900527296927, 
-0.273160210918771, -0.682900527296927, -0.478030369107849, 0.136580105459385, 
0.75119058002662, 0.546320421837542, 0.341450263648464, -0.887770685486005, 
-0.0682900527296927, 0.136580105459385, 0.75119058002662, -0.273160210918771, 
-0.682900527296927, 0.136580105459385, -0.478030369107849, -0.273160210918771, 
-0.273160210918771, 0.136580105459385, 0.341450263648464, -0.478030369107849, 
-0.0682900527296927, -0.682900527296927, 0.75119058002662, -0.273160210918771, 
-0.478030369107849, -0.0682900527296927, -0.0682900527296927, 
-0.273160210918771, -0.0682900527296927, -0.478030369107849, 
0.75119058002662, -0.0682900527296927, 0.136580105459385, 0.546320421837542, 
0.546320421837542, -0.478030369107849, -0.273160210918771, 0.546320421837542, 
-0.478030369107849, -0.682900527296927, 0.75119058002662, -0.0682900527296927, 
-0.682900527296927, -0.682900527296927, 0.75119058002662, 0.341450263648464, 
-0.478030369107849, 0.75119058002662, 0.136580105459385, -0.887770685486005, 
0.341450263648464, 0.341450263648464, 0.546320421837542, -0.273160210918771, 
0.136580105459385, 0.75119058002662, -0.0682900527296927, -0.682900527296927, 
-0.478030369107849, -0.478030369107849, 0.75119058002662, 0.546320421837542, 
-0.478030369107849, 0.546320421837542, 0.136580105459385, -0.887770685486005, 
0.75119058002662, -0.0682900527296927, 0.75119058002662, 0.75119058002662, 
-0.273160210918771, -0.682900527296927, 0.546320421837542, 0.546320421837542, 
-0.887770685486005, 0.75119058002662, -0.273160210918771, 0.546320421837542, 
-0.0682900527296927, 0.136580105459385, 0.341450263648464, -0.478030369107849, 
0.136580105459385, 0.136580105459385, -0.273160210918771, 0.546320421837542, 
-0.273160210918771, -0.273160210918771, -0.273160210918771, 0.75119058002662, 
-0.887770685486005, -0.887770685486005, -0.0682900527296927, 
-0.478030369107849, -0.0682900527296927, 0.75119058002662, -0.273160210918771, 
0.136580105459385, -0.478030369107849, -0.273160210918771, 0.136580105459385, 
0.75119058002662, 0.546320421837542, -0.478030369107849, -0.273160210918771, 
-0.273160210918771, 0.136580105459385, -0.273160210918771, -0.0682900527296927, 
0.75119058002662, 0.136580105459385), resp.var = c(2L, 1L, 0L, 
1L, 0L, 0L, 0L, 0L, 0L, 1L, 3L, 1L, 0L, 1L, 0L, 1L, 2L, 0L, 1L, 
0L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 1L, 0L, 0L, 0L, 2L, 
1L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 1L, 0L, 2L, 
0L, 3L, 2L, 0L, 2L, 2L, 0L, 0L, 0L, 1L, 1L, 3L, 1L, 2L, 0L, 1L, 
0L, 0L, 1L, 0L, 2L, 0L, 2L, 4L, 0L, 1L, 0L, 0L, 0L, 0L, 0L, 2L, 
3L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 1L, 0L, 0L, 0L, 0L, 0L, 1L, 2L, 
0L, 0L, 0L, 0L, 1L, 1L, 0L, 1L, 0L, 2L, 0L, 1L, 0L, 4L, 1L, 0L, 
1L, 1L, 0L, 0L, 0L, 1L, 3L, 0L, 2L, 0L, 0L, 2L, 1L, 0L, 0L, 2L, 
0L, 0L, 0L, 2L, 0L, 0L, 3L, 0L, 0L, 2L, 1L, 1L, 0L, 0L, 3L, 1L, 
1L, 2L, 0L, 2L, 0L, 2L, 2L, 0L, 1L, 0L, 0L, 0L, 0L, 1L, 0L, 0L, 
0L, 0L, 0L, 0L, 0L, 0L, 0L, 1L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 
0L, 0L, 0L, 0L, 0L, 1L, 0L, 0L, 1L, 0L, 2L, 2L, 1L, 0L, 0L, 1L, 
0L, 0L, 0L, 0L, 6L, 1L, 0L, 1L, 0L, 0L, 0L, 0L, 2L, 0L, 0L, 0L, 
1L, 0L, 0L, 1L, 3L, 1L, 0L, 2L, 3L, 0L, 0L, 1L, 0L, 0L, 1L, 1L, 
0L, 0L, 0L, 0L, 1L, 2L, 1L, 1L, 0L, 0L, 2L, 0L, 2L, 0L, 0L, 1L, 
1L, 0L, 0L, 2L, 0L, 1L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 1L, 0L, 
0L, 1L, 0L, 2L, 1L, 0L, 1L, 0L, 1L, 1L, 0L, 1L, 0L, 0L, 0L, 0L, 
0L, 3L, 0L, 0L, 3L, 0L, 0L, 1L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 
0L, 2L, 1L, 1L, 0L, 2L, 2L, 0L, 2L, 1L, 0L, 2L, 0L, 0L, 0L, 0L, 
3L, 0L, 2L, 0L, 0L, 0L, 0L, 2L, 0L, 0L, 2L, 0L, 1L, 1L, 0L, 1L, 
0L, 3L, 1L, 3L, 1L, 0L, 0L, 0L, 0L, 0L, 0L, 1L, 0L, 0L, 2L, 0L, 
2L, 0L, 0L, 0L, 0L, 0L, 0L, 0L, 2L, 0L, 2L, 0L, 3L, 0L, 0L, 0L, 
0L, 1L, 0L, 0L, 3L, 1L, 1L, 2L, 0L, 0L, 3L, 0L, 0L, 0L, 1L, 1L, 
0L, 1L, 3L, 0L, 2L, 0L, 0L, 1L, 3L, 1L, 0L, 0L, 4L, 3L, 0L, 2L, 
0L, 0L, 0L, 3L, 0L, 0L, 2L, 3L, 0L, 1L, 0L, 1L, 0L, 1L, 0L, 0L, 
0L, 0L, 0L, 3L, 3L, 2L, 0L, 0L, 2L, 0L, 0L, 0L, 0L, 2L, 0L, 0L, 
0L, 0L, 0L, 1L, 0L, 2L, 0L, 0L, 1L, 0L, 0L, 1L, 2L, 0L, 1L, 0L, 
2L, 1L, 0L, 1L, 1L, 0L, 0L, 0L, 0L, 3L, 1L, 0L, 0L, 0L, 0L, 0L, 
1L, 2L, 0L, 2L, 0L, 1L, 0L, 1L, 0L, 0L, 0L, 1L, 0L, 0L, 0L, 1L, 
0L, 0L, 3L, 2L, 2L, 0L, 1L, 0L, 5L, 0L, 4L, 2L, 0L, 3L, 0L, 0L, 
1L, 1L, 0L, 0L, 0L, 2L, 0L, 1L, 0L, 3L, 0L, 2L, 0L, 0L, 0L, 2L, 
0L), rand.eff = c(37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 
37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 
37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 
37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 
37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 
37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 
37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 
37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 
37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 
37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 
37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 
37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 
37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 
37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 37L, 
37L, 37L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 
40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 
40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 
40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 
40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 
40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 
40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 
40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 
40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 
40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 
40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 
40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 
40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 
40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 40L, 
43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 
43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 
43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 
43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 
43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 
43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 
43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 
43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 
43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 
43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 
43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L, 43L)), .Names = c("cat.var", 
"cont.var", "resp.var", "rand.eff"), row.names = c(NA, 500L), class = "data.frame")

not too hard by combining `predict` with `ggplot` or `lattice::xyplot`. Reproducible example please? — Ben Bolker, May 05 '12 at 01:22

score 16 · Accepted Answer · answered May 05 '12 at 14:03

Here's an answer of sorts (by the way, you had some missing quotation marks in your data frame above, which had to be fixed manually ...)

Fit the model:

library(lme4)
fit <- glmer(resp.var ~ cont.var:cat.var + (1|rand.eff) ,
           data = sample.data , poisson)

(Note that this is a slightly weird model specification -- forces all categories to have the same value at cont.var==0. Did you mean cont.var*cat.var?

library(ggplot2)
theme_update(theme_bw())  ## set white rather than gray background

Quick and dirty linear regressions:

ggplot(sample.data,aes(cont.var,resp.var,linetype=cat.var))+
    geom_smooth(method="lm",se=FALSE)

Now with a Poisson GLM (but not incorporating the random effect), and showing the data points:

ggplot(sample.data,aes(cont.var,resp.var,colour=cat.var))+
    stat_sum(aes(size=..n..),alpha=0.5)+
    geom_smooth(method="glm",family="poisson")

The next bit requires the development (r-forge) version of lme4, which has a predict method:

Set up data frame for prediction:

predframe <- with(sample.data,
                  expand.grid(cat.var=levels(cat.var),
                              cont.var=seq(min(cont.var),
                              max(cont.var),length=51)))

Predict at population level (REform=NA), on the linear predictor (logit) scale (this is the only way you will get straight lines on the plot)

predframe$pred.logit <- predict(fit,newdata=predframe,REform=NA)

minmaxvals <- range(sample.data$cont.var)

ggplot(predframe,aes(cont.var,pred.logit,linetype=cat.var))+geom_line()+
    geom_point(data=subset(predframe,cont.var %in% minmaxvals),
               aes(shape=cat.var))

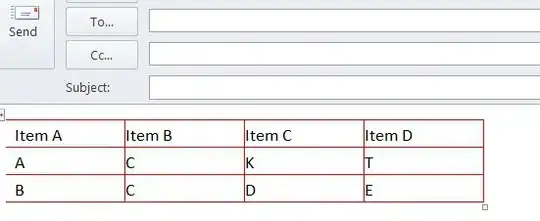enter image description here Now on the response scale:

predframe$pred <- predict(fit,newdata=predframe,REform=NA,type="response")
ggplot(predframe,aes(cont.var,pred,linetype=cat.var))+geom_line()+
    geom_point(data=subset(predframe,cont.var %in% minmaxvals),
               aes(shape=cat.var))

enter image description here

Thanks! Sorry about the missing quotes. I used dput, and didn't modify the output, to provided the sample data. Should I have done something else. And yes, you are right, I should have used `*` instead of `:` in specifying the model. — Jota, May 05 '12 at 18:28
It's all a little confusing, but I would try `install.packages("lme4",repos="http://lme4.r-forge.r-project.org/repos")` -- the build on the main r-forge repository is broken at the moment (you can always re-install from CRAN if necessary). — Ben Bolker, May 05 '12 at 23:30
Anything but Excel :-) : what are the symptoms of your inability to install? (What OS and R version are you using?) — Ben Bolker, May 07 '12 at 02:15

score 3 · Answer 2 · answered Oct 16 '17 at 13:51

3

The jtools package (CRAN link) can make the plotting of this sort of model pretty straightforward. I'm the developer of that package.

We will fit the model like Ben did in his answer:

library(lme4)
fit <- glmer(resp.var ~ cont.var:cat.var + (1 | rand.eff),
             data = sample.data, family = poisson)

And with jtools we just use the interact_plot function like this:

library(jtools)
interact_plot(fit, pred = cont.var, modx = cat.var)

The result:

By default it plots on the response scale, but you can have it plotted on the linear scale with the outcome.scale = "link" argument (default is "response").

answered Oct 16 '17 at 13:51

commscho

380
2
7

I get a loong list of warnings when trying to install jtools, posted a bit of such: InternetOpenUrl failed: 'The date in the certificate is invalid or has expired' cannot open URL 'https://mirror.its.dal.ca/cran/src/contrib/PACKAGES' I unable to access index for repository https://mirror.its.dal.ca/cran/src/contrib: cannot open URL 'https://mirror.its.dal.ca/cran/src/contrib/PACKAGES' package ‘jtools’ is not available (for R version 3.6.3) InternetOpenUrl failed: 'The date in the certificate is invalid or has expired' – Agus camacho Apr 12 '21 at 16:43

score 1 · Answer 3 · edited Jun 20 '20 at 09:12

1

The effects package has support for lme4 models, and should be able to do what you want.

effects: Effect Displays for Linear, Generalized Linear, and Other Models

Graphical and tabular effect displays, e.g., of interactions, for various statistical models with linear predictors.

It also comes with two slightly outdated papers (you can think of them as vignettes).

edited Jun 20 '20 at 09:12

Community

1
1

answered Feb 06 '15 at 21:58

landroni

2,902
1
32
39

R: Interaction Plot with a continuous and a categorical variable for a GLMM (lme4)

3 Answers3

Linked