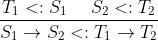Confused about function subtyping

Question

I'm taking a course on programming languages and the answer to "when is a function a sub type of another function" is very counter-intuitive to me.

To clarify: suppose that we have the following type relation:

bool<int<real

Why is the function (real->bool) a subtype of (int->bool)? Shouldn't it be the other way around?

I would expect the criteria for sub typing functions to be: f1 is a subtype of f2 if f2 can take any argument that f1 can take, and f1 returns only values that f2 returns. There clearly are values that f1 can take, but f2 can't.

Answer 1

Here's the rule for function sub-typing:

Argument types must be contra-variant, return types must be co-variant.

Co-variant == preserves the "A is a subtype of B" hierarchy for the type of the results parameter.

Contra-variant == reverses ("goes against") the type hierarchy for the arguments parameter.

So, in your example:

f1:  int  -> bool
f2:  real -> bool

We can safely conclude that f2 is a subtype of f1. Why? Because (1) looking at just the argument types for both functions, we see that the type hierarchy of "bool is a subtype of int" is in fact co-variant. It preserves the type hierarchy between ints and bools. (2) looking at just the results types for both functions, we see that contra-variance is upheld.

Put another way (the plain English way I think about this subject):

contra-variant arguments: "my caller can pass in more than I require, but that's okay, because I'll use only what I need to use." co-variant return values: "I can return more than the caller requires, but that's okay, he/she will just use what they need, and will ignore the rest"

Let's look at another examples, using structs where everything is an integer:

f1:  {x,y,z} -> {x,y}
f2:  {x,y}   -> {x,y,z}

So here again, we're asserting that f2 is a subtype of f1 (which it is). Looking at the argument types for both functions (and using the < symbol to denote "is a subtype of"), then if f2 < f1, is {x,y,z} < {x,y} ? The answer is yes. {x,y,z} is co-variant with {x,y}. i.e. in defining the struct {x,y,z} we "inherited" from the {x,y} struct, but added a third member, z.

Looking at the return types for both functions, if f2 < f1, then is {x,y} > {x,y,z}? The answer again is yes. (See above logic).

Yet a third way to think about this, is to assume f2 < f1, then try various casting scenarios, and see if everything works. Example (psuedo-code):

   F1 = f1;
   F2 = f2;
   {a,b}   = F1({1,2,3});  // call F1 with a {x,y,z} struct of {1,2,3};  This works.
   {a,b,c} = F2({1,2});    // call F2 with a {x,y} struct of {1,2}.  This also works.
   
   // Now take F2, but treat it like an F1.  (Which we should be able to do, 
   // right?  Because F2 is a subtype of F1).  Now pass it in the argument type 
   // F1 expects.  Does our assignment still work?  It does.
   {a,b} = ((F1) F2)({1,2,3});

Answer 2

Here's another answer because, while I understood how the function subtype rules made sense, I wanted to work through why any other combination of argument/result subtyping did not.

---

The subtype rule is:

Meaning that if the top subtype conditions are met, then the bottom holds true.

In the function type definition, the function arguments are contravariant, since we've reversed the subtype relation between T1 and S1. The function results are covariant because they preserve the subtype relation between T2 and S2.

With the definition out of the way, why is the rule like this? It's well stated in Aaron Fi's answer, and I also found the definition here (search for the heading "Function Types"):

An alternative view is that it is safe to allow a function of one type S1 → S2 to be used in a context where another type T1 → T2 is expected as long as none of the arguments that may be passed to the function in this context will surprise it (T1 <: S1) and none of the results that it returns will surprise the context (S2 <: T2).

Again, that made sense to me, but I wanted to see why no other combination of typing rules made sense. To do this I looked at a simple higher order function and some example record types.

For all examples below, let:

1. S1 := {x, y}
2. T1 := {x, y, z}
3. T2 := {a}
4. S2 := {a, b}

Example with contravariant argument types and covariant return types

Let:

1. f1 have type S1 → S2 ⟹ {x, y} → {a, b}
2. f2 have type T1 → T2 ⟹ {x, y, z} → {a}

Now assume that type(f1) <: type(f2). We know this from the rule above, but let's pretend we don't and just see why it makes sense.

We run map( f2 : {x, y, z} → {a}, L : [ {x, y, z} ] ) : [ {a} ]

If we replace f2 with f1 we get:

map( f1 : {x, y} → {a, b}, L : [ {x, y, z} ] ) : [ {a, b} ]

This works out fine because:

1. Whatever the function f1 does with its argument, it can ignore the extra z record field and have no problems.
2. Whatever the context running map does with the results, it can ignore the extra b record field and have no problems.

Concluding:

{x, y} → {a, b} ⟹ {x, y, z} → {a} ✔

Example with covariant argument types and covariant return types

Let:

1. f1 have type T1 → S2 ⟹ {x, y, z} → {a, b}
2. f2 have type S1 → T2 ⟹ {x, y} → {a}

Assume type(f1) <: type(f2)

We run map( f2 : {x, y} → {a}, L : [ {x, y} ] ) : [ {a} ]

If we replace f2 with f1 we get:

map( f1 : {x, y, z} → {a, b}, L : [ {x, y} ] ) : [ {a, b} ]

We can run into a problem here because f1 expects and might operate on the z record field, and such a field is not present in any records in list L. ⚡

Example with contravariant argument types and contravariant return types

Let:

1. f1 have type S1 → T2 ⟹ {x, y} → {a}
2. f2 have type T1 → S2 ⟹ {x, y, z} → {a, b}

Assume type(f1) <: type(f2)

We run map( f2 : {x, y, z} → {a, b}, L : [ {x, y, z} ] ) : [ {a, b} ]

If we replace f2 with f1 we get:

map( f1 : {x, y} → {a}, L : [ {x, y, z} ] ) : [ {a} ]

We have no issue with ignoring the z record field when passed into f1, but if the context that calls map expects the a list of records with a b field, we will hit an error. ⚡

Example with covariant argument types and contravariant return

Look at the above examples for the two places this could go wrong.

Conclusion

This is a very long and verbose answer, but I had to jot this stuff down to figure out why other argument and return parameter subtyping was invalid. Since I had it somewhat written down, I figured why not post it here.

Answer 3

I've been struggling finding my own answer to this same question because I did not find it intuitive by just accepting the substitution rules. So here is my attempt:

By definition: function f1: A1 => B1 is a supertype of f2: A2 => B2 if f2 can be used in places that require f1.

Now look at the following diagram, imagine water flows from top to bottom through funnels f1 and f2.

We realize that if we want to replace the funnel f1 with another funnel f2, then:

• Input diameter A2 must be no smaller than A1.
• Output diameter B2 needs to be no bigger than B1.

The same reasoning applies to functions: in order for f2 to be able to replace f1, then:

• Input set A2 of f2 needs to cover all possible inputs of f1, i.e. A1 <: A2, and
• Output set B2 of f2 needs to fit in what is required for f1, i.e. B2 <: B1

To put it another way: If A1 <: A2 and B1 >: B2 then f1: A1 => B1 >: f2: A2 => B2

Answer 4

The question is answered, but I'd like to present here an easy example (regarding the argument type, which is the unintuitive one).

The below code will fail, because you can pass only Strings to myFuncB, and we are passing numbers and booleans.

typedef FuncTypeA = Object Function(Object obj); // (Object) => Object
typedef FuncTypeB = String Function(String name); // (String) => String

void process(FuncTypeA myFunc) {
   myFunc("Bob").toString(); // Ok.
   myFunc(123).toString(); // Fail.
   myFunc(true).toString(); // Fail.
}

FuncTypeB myFuncB = (String name) => name.toUpperCase();

process(myFuncB);

However, the below code will work, because now you can pass objects of any type to myFuncB, and we only pass Strings.

typedef FuncTypeA = Object Function(String name); // (String) => Object
typedef FuncTypeB = String Function(Object obj); // (Object) => String

void process(FuncTypeA myFuncA) {
   myFunc("Bob").toString(); // Ok.
   myFunc("Alice").toString(); // Ok.
}

FuncTypeB myFuncB = (Object obj) => obj.toString();

process(myFuncB);

Answer 5

Borrowing from TAPL:

S is a subtype of T, i.e., S <: T if any term of type S can be used in a context where a term of type T is expected. Applying this to function subtyping F <: G means any function of type F can be used in a context where a function of type G is expected.

Other intuitions of subtyping are:

1. every value described by S is also described by T

2. the elements of S are a subset of elements of T

Let's use intuition 2. for the following function subtyping to check when is it safe to use $ S_1 \to S_2 $ in a context where $ T_1 \to T_2$ is expected.

In order to be compatible with the expected function $ T_1 \to T_2$, we can immediately see that the arguments $ S_1 $ should be a superset of $ T_1 $, i.e., all required arguments should definitely be present, extra arguments can be present, we can simply not process the extra arguments; and the return values $ S_2 $ should be subset of $ T_2 $ in order to not surprise the context where $ T_1 \to T_2$ is generally invoked / applied.