Linear time algorithm for 2-SUM

Question

Given an integer x and a sorted array a of N distinct integers, design a linear-time algorithm to determine if there exists two distinct indices i and j such that a[i] + a[j] == x

Answer 1

This is type of Subset sum problem

Here is my solution. I don't know if it was known earlier or not. Imagine 3D plot of function of two variables i and j:

sum(i,j) = a[i]+a[j]

For every i there is such j that a[i]+a[j] is closest to x. All these (i,j) pairs form closest-to-x line. We just need to walk along this line and look for a[i]+a[j] == x:

 int i = 0; 
 int j = lower_bound(a.begin(), a.end(), x)  -  a.begin(); 
 while (j >= 0 && j < a.size()  &&  i < a.size())  {  
    int sum = a[i]+a[j]; 
    if (sum == x)   { 
        cout << "found: " << i << " " << j << endl;  
        return;
    }
    if (sum > x)    j--;
    else            i++;
    if (i > j) break;
 }  
 cout << " not found\n";

Complexity: O(n)

Answer 2

think in terms of complements.

iterate over the list, figure out for each item what the number needed to get to X for that number is. stick number and complement into hash. while iterating check to see if number or its complement is in hash. if so, found.

edit: and as I have some time, some pseudo'ish code.

boolean find(int[] array, int x) {
    HashSet<Integer> s = new HashSet<Integer>();

    for(int i = 0; i < array.length; i++) {
        if (s.contains(array[i]) || s.contains(x-array[i])) {
            return true;
        }
        s.add(array[i]);
        s.add(x-array[i]);
    }
    return false;
}

Answer 3

Given that the array is sorted (WLOG in descending order), we can do the following: Algorithm A_1: We are given (a_1,...,a_n,m), a_1<...,<a_n. Put a pointer at the top of the list and one at the bottom. Compute the sum where both pointers are. If the sum is greater than m, move the above pointer down. If the sum is less than m, move the lower pointer up. If a pointer is on the other (here we assume each number can be employed only once), report unsat. Otherwise, (an equivalent sum will be found), report sat.

It is clear that this is O(n) since the maximum number of sums computed is exactly n. The proof of correctness is left as an exercise.

This is merely a subroutine of the Horowitz and Sahni (1974) algorithm for SUBSET-SUM. (However, note that almost all general purpose SS algorithms contain such a routine, Schroeppel, Shamir (1981), Howgrave-Graham_Joux (2010), Becker-Joux (2011).)

If we were given an unordered list, implementing this algorithm would be O(nlogn) since we could sort the list using Mergesort, then apply A_1.

Answer 4

1. First pass search for the first value that is > ceil(x/2). Lets call this value L.
2. From index of L, search backwards till you find the other operand that matches the sum.

It is 2*n ~ O(n)

This we can extend to binary search.

1. Search for an element using binary search such that we find L, such that L is min(elements in a > ceil(x/2)).

2. Do the same for R, but now with L as the max size of searchable elements in the array.

This approach is 2*log(n).

Answer 5

Here's a python version using Dictionary data structure and number complement. This has linear running time(Order of N: O(N)):

def twoSum(N, x):
    dict = {}

    for i in range(len(N)):
        complement = x - N[i]
        if complement in dict:
            return True
        dict[N[i]] = i

    return False

# Test
print twoSum([2, 7, 11, 15], 9) # True
print twoSum([2, 7, 11, 15], 3) # False

Answer 6

Iterate over the array and save the qualified numbers and their indices into the map. The time complexity of this algorithm is O(n).

vector<int> twoSum(vector<int> &numbers, int target) {
    map<int, int> summap;
    vector<int> result;
    for (int i = 0; i < numbers.size(); i++) {
        summap[numbers[i]] = i;
    }
    for (int i = 0; i < numbers.size(); i++) {
        int searched = target - numbers[i];
        if (summap.find(searched) != summap.end()) {
            result.push_back(i + 1);
            result.push_back(summap[searched] + 1);
            break;
        }
    }
    return result;
}

Answer 7

I would just add the difference to a HashSet<T> like this:

public static bool Find(int[] array, int toReach)
{
    HashSet<int> hashSet = new HashSet<int>();

    foreach (int current in array)
    {
        if (hashSet.Contains(current))
        {
            return true;
        }
        hashSet.Add(toReach - current);
    }
    return false;
}

Answer 8

Note: The code is mine but the test file was not. Also, this idea for the hash function comes from various readings on the net.

An implementation in Scala. It uses a hashMap and a custom (yet simple) mapping for the values. I agree that it does not makes use of the sorted nature of the initial array.

The hash function

I fix the bucket size by dividing each value by 10000. That number could vary, depending on the size you want for the buckets, which can be made optimal depending on the input range.

So for example, key 1 is responsible for all the integers from 1 to 9.

Impact on search scope

What that means, is that for a current value n, for which you're looking to find a complement c such as n + c = x (x being the element you're trying ton find a 2-SUM of), there is only 3 possibles buckets in which the complement can be:

• -key
• -key + 1
• -key - 1

Let's say that your numbers are in a file of the following form:

0
1
10
10
-10
10000
-10000
10001
9999
-10001
-9999
10000
5000
5000
-5000
-1
1000
2000
-1000
-2000

Here's the implementation in Scala

import scala.collection.mutable                                                                                                                                                                       
import scala.io.Source

object TwoSumRed {
  val usage = """ 
    Usage: scala TwoSumRed.scala [filename]
  """

  def main(args: Array[String]) {
    val carte = createMap(args) match {
      case None => return
      case Some(m) => m
    }

    var t: Int = 1

    carte.foreach {
      case (bucket, values) => {
        var toCheck: Array[Long] = Array[Long]() 

        if (carte.contains(-bucket)) {
          toCheck = toCheck ++: carte(-bucket)
        }
        if (carte.contains(-bucket - 1)) {
          toCheck = toCheck ++: carte(-bucket - 1)
        }
        if (carte.contains(-bucket + 1)) {
          toCheck = toCheck ++: carte(-bucket + 1)
        }

        values.foreach { v =>
          toCheck.foreach { c =>
            if ((c + v) == t) {
              println(s"$c and $v forms a 2-sum for $t")
              return
            }
          }
        }
      }
    }
  }

  def createMap(args: Array[String]): Option[mutable.HashMap[Int, Array[Long]]] = {
    var carte: mutable.HashMap[Int,Array[Long]] = mutable.HashMap[Int,Array[Long]]()

    if (args.length == 1) {
      val filename = args.toList(0)
      val lines: List[Long] = Source.fromFile(filename).getLines().map(_.toLong).toList
      lines.foreach { l =>
        val idx: Int = math.floor(l / 10000).toInt
        if (carte.contains(idx)) {
          carte(idx) = carte(idx) :+ l
        } else {
          carte += (idx -> Array[Long](l))
        }
      }
      Some(carte)
    } else {
      println(usage)
      None
    }
  }
}

Answer 9

int[] b = new int[N];
for (int i = 0; i < N; i++)
{
    b[i] = x - a[N -1 - i];
}
for (int i = 0, j = 0; i < N && j < N;)
    if(a[i] == b[j])
    {
       cout << "found";
       return;
     } else if(a[i] < b[j])
        i++;
     else
        j++;
cout << "not found";

Answer 10

Here is a linear time complexity solution O(n) time O(1) space

 public void twoSum(int[] arr){

   if(arr.length < 2) return;

   int max = arr[0] + arr[1];
   int bigger = Math.max(arr[0], arr[1]);
   int smaller = Math.min(arr[0], arr[1]);
   int biggerIndex = 0;
   int smallerIndex = 0;

    for(int i = 2 ; i < arr.length ; i++){

        if(arr[i] + bigger <= max){ continue;}
        else{
            if(arr[i] > bigger){
                smaller = bigger;
                bigger = arr[i];
                biggerIndex = i;
            }else if(arr[i] > smaller)
            {
                smaller = arr[i];
                smallerIndex = i;
            }
            max = bigger + smaller;
        }

    }

    System.out.println("Biggest sum is: " + max + "with indices ["+biggerIndex+","+smallerIndex+"]");

}

Answer 11

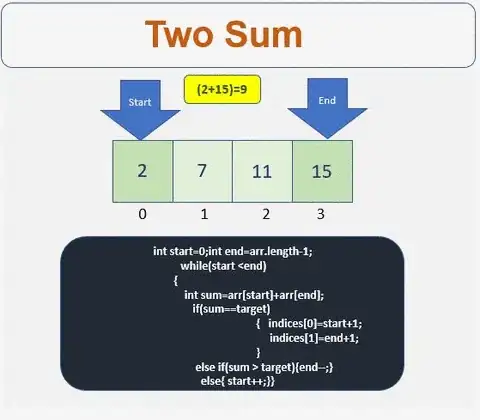
Solution

• We need array to store the indices
• Check if the array is empty or contains less than 2 elements
• Define the start and the end point of the array
• Iterate till condition is met
• Check if the sum is equal to the target. If yes get the indices.
• If condition is not met then traverse left or right based on the sum value
• Traverse to the right
• Traverse to the left

For more info :[http://www.prathapkudupublog.com/2017/05/two-sum-ii-input-array-is-sorted.html

Answer 12

Credit to leonid

His solution in java, if you want to give it a shot

I removed the return, so if the array is sorted, but DOES allow duplicates, it still gives pairs

static boolean cpp(int[] a, int x) {
    int i = 0;
    int j = a.length - 1;
    while (j >= 0 && j < a.length && i < a.length) {
        int sum = a[i] + a[j];
        if (sum == x) {
        System.out.printf("found %s, %s \n", i, j);
//                return true;
        }
        if (sum > x) j--;
        else i++;
        if (i > j) break;
    }
    System.out.println("not found");
    return false;
    }

Answer 13

The classic linear time two-pointer solution does not require hashing so can solve related problems such as approximate sum (find closest pair sum to target).

First, a simple n log n solution: walk through array elements a[i], and use binary search to find the best a[j].

To get rid of the log factor, use the following observation: as the list is sorted, iterating through indices i gives a[i] is increasing, so any corresponding a[j] is decreasing in value and in index j. This gives the two-pointer solution: start with indices lo = 0, hi = N-1 (pointing to a[0] and a[N-1]). For a[0], find the best a[hi] by decreasing hi. Then increment lo and for each a[lo], decrease hi until a[lo] + a[hi] is the best. The algorithm can stop when it reaches lo == hi.