Checking odd/even numbers and changing outputs on number size

Question

I have a couple of problems to solve for an assignment, and am a bit stuck. The question is to write a program that gets the user to input an odd number (check it's odd), then print an upside down pyramid of stars based on the size of the input.

For example, if you enter 5, it comes up with

*****
 ***
  *

My problem is therefore two-fold.

1) How do I check if it's even or odd? I tried if number/2 == int in the hope that it might do something, and the internet tells me to do if number%2==0, but that doesn't work.

2) How do I change the asterisks in the middle of each line?

Any help with either problem is greatly appreciated.

Answer 1

Giving you the complete answer would have no point at all since this is homework, so here are a few pointers :

Even or Odd:

number % 2 == 0

definitely is a very good way to find whether your number is even.

In case you do not know %, this does modulo which is here the remainder of the division of number by 2. http://en.wikipedia.org/wiki/Modulo_operation

Printing the pyramid:

First advice: In order to print *****, you can do print "*" * 5.

Second advice: In order to center the asterisks, you need to find out how many spaces to write before the asterisks. Then you can print a bunch of spaces and asterisks with print " "*1 + "*"*3

Answer 2

The modulo 2 solutions with %2 is good, but that requires a division and a subtraction. Because computers use binary arithmetic, a much more efficient solution is:

# This first solution does not produce a Boolean value. 
is_odd_if_zero = value & 1

# or

is_odd = (value & 1) == 1

# or

is_even = (value & 1) == 0

Answer 3

A few of the solutions here reference the time taken for various "is even" operations, specifically n % 2 vs n & 1, without systematically checking how this varies with the size of n, which turns out to be predictive of speed.

The short answer is that if you're using reasonably sized numbers, normally < 1e9, it doesn't make much difference. If you're using larger numbers then you probably want to be using the bitwise operator.

Here's a plot to demonstrate what's going on (with Python 3.7.3, under Linux 5.1.2):

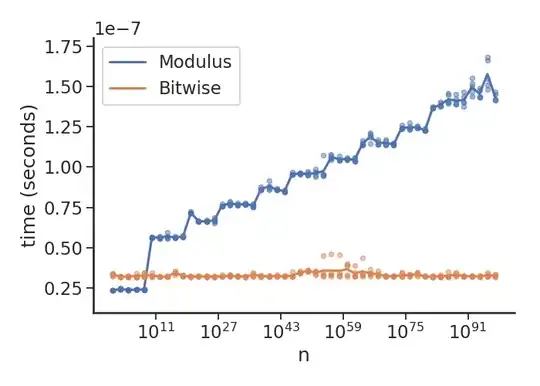
Basically as you hit "arbitrary precision" longs things get progressively slower for modulus, while remaining constant for the bitwise op. Also, note the 10**-7 multiplier on this, i.e. I can do ~30 million (small integer) checks per second.

Here's the same plot for Python 2.7.16:

which shows the optimisation that's gone into newer versions of Python.

I've only got these versions of Python on my machine, but could rerun for other versions of there's interest. There are 51 ns between 1 and 1e100 (evenly spaced on a log scale), for each point I do the equivalent of:

timeit('n % 2', f'n={n}', number=niter) 

where niter is calculated to make timeit take ~0.1 seconds, and this is repeated 5 times. The slightly awkward handling of n is to make sure we're not also benchmarking global variable lookup, which is slower than local variables. The mean of these values are used to draw the line, and the individual values are drawn as points.

Answer 4

Simple but yet fast:

>>> def is_odd(a):
...     return bool(a - ((a>>1)<<1))
...
>>> print(is_odd(13))
True
>>> print(is_odd(12))
False
>>>

Or even simpler:

>>> def is_odd(a):
...   return bool(a & 1)

Answer 5

1) How do I check if it's even or odd? I tried "if number/2 == int" in the hope that it might do something, and the internet tells me to do "if number%2==0", but that doesn't work.

def isEven(number):
        return number % 2 == 0

Answer 6

if number%2==0

will tell you that it's even. So odd numbers would be the else statement there. The "%" is the mod sign which returns the remainder after dividing. So essentially we're saying if the number is divisible by two we can safely assume it's even. Otherwise it's odd (it's a perfect correlation!)

As for the asterisk placing you want to prepend the asterisks with the number of spaces correlated to the line it's on. In your example

***** line 0
***   line 1
*     line 2

We'll want to space accordingly

0*****
01***
012*

Answer 7

la = lambda x : "even" if not x % 2 else "odd"

Answer 8

I guess the easiest and most basic way is this

import math

number = int (input ('Enter number: '))

if number % 2 == 0 and number != 0:
    print ('Even number')
elif number == 0:
    print ('Zero is neither even, nor odd.')
else:
    print ('Odd number')

Just basic conditions and math. It also minds zero, which is neither even, nor odd and you give any number you want by input so it's very variable.

Answer 9

Regarding the printout, here's how I would do it using the Format Specification Mini Language (section: Aligning the text and specifying a width):

Once you have your length, say length = 11:

rowstring = '{{: ^{length:d}}}'.format(length = length) # center aligned, space-padded format string of length <length>
for i in xrange(length, 0, -2): # iterate from top to bottom with step size 2
    print rowstring.format( '*' * i )

Answer 10

there are a lot of ways to check if an int value is odd or even. I'll show you the two main ways:

number = 5

def best_way(number):
    if number%2==0:
        print "even"
    else:
        print "odd"

def binary_way(number):
    if str(bin(number))[len(bin(number))-1]=='0':
        print "even"
    else:
        print "odd"
best_way(number)
binary_way(number)

hope it helps

Answer 11

Here's my solution:

def is_even(n):
    r=n/2.0
    return True if r==int(r) else False

Answer 12

def main():
    n = float(input('odd:'))
    while n % 2 == 0:
        #if n % 2 == 1: No need for these lines as if it were true the while loop would not have been entered.
            #break not required as the while condition will break loop
        n = float(input('odd:'))


    for i in range(int((n+1)/2)):
        print(' '*i+'*'*int((n-2*i))+' '*i)

main()

#1st part ensures that it is an odd number that was entered.2nd part does the printing of triangular

Answer 13

Sample Instruction Given an integer, n, performing the following conditional actions:

• If n is odd, print Weird
• If n is even and in the inclusive range of 2 to 5, print Not Weird
• If n is even and in the inclusive range of 6 to 20, print Weird
• If n is even and greater than 20, print Not Weird

import math
n = int(input())

if n % 2 ==1:
    print("Weird")
elif n % 2==0 and n in range(2,6):
    print("Not Weird")
elif n % 2 == 0 and n in range(6,21):
    print("Weird")
elif n % 2==0 and n>20:
    print("Not Weird")

Answer 14

This is simple code. You can try it and grab the knowledge easily.

n = int(input('Enter integer : '))
    if n % 2 == 3`8huhubuiiujji`:
        print('digit entered is ODD')
    elif n % 2 == 0 and 2 < n < 5:
        print('EVEN AND in between [2,5]')
    elif n % 2 == 0 and 6 < n < 20:
        print('EVEN and in between [6,20]')
    elif n % 2 == 0 and n > 20:
       print('Even and greater than 20')

and so on...

Answer 15

Modulus method is the usual method. We can also do this to check if odd or even:

def f(a):
    if (a//2)*2 == a:
        return 'even'
    else:
        return 'odd'

Integer division by 2 followed by multiplication by two.

Answer 16

My solution basically we have two string and with the & we get the right index:

res = ["Even", "Odd"]
print(res[x & 1])

Please note that it seems slower than other alternatives:

#!/usr/bin/env python3
import math
import random
from timeit import timeit

res = ["Even", "Odd"]

def foo(x):
    return res[x & 1]

def bar(x):
    if x & 1:
        return "Odd"
    return "Even"

la = lambda x : "Even" if not x % 2 else "Odd"

iter = 10000000

time = timeit('bar(random.randint(1, 1000))', "from __main__ import bar, random", number=iter)
print(time)
time = timeit('la(random.randint(1, 1000))', "from __main__ import la, random", number=iter)
print(time)
time = timeit('foo(random.randint(1, 1000))', "from __main__ import foo, random", number=iter)
print(time)

output:
8.05739480999182
8.170479692984372
8.892275177990086

Answer 17

1. another odd testing function

Ok, the assignment was handed in 8+ years ago, but here is another solution based on bit shifting operations:

def isodd(i):
    return(bool(i>>0&1))

testing gives:

>>> isodd(2)
False
>>> isodd(3)
True
>>> isodd(4)
False

2. Nearest Odd number alternative approach

However, instead of a code that says "give me this precise input (an integer odd number) or otherwise I won't do anything" I also like robust codes that say, "give me a number, any number, and I'll give you the nearest pyramid to that number".

In that case this function is helpful, and gives you the nearest odd (e.g. any number f such that 6<=f<8 is set to 7 and so on.)

def nearodd(f):
    return int(f/2)*2+1

Example output:

nearodd(4.9)
5

nearodd(7.2)
7

nearodd(8)
9  

Answer 18

This the function

def oddOrEven(num):
    if num%2 == 0:
        print("even")

    else: 
        for i in range(num):
            for j in range(i+1):
                print(" ", end="")
            for m in range(num-i, 0, -1):
                print("* ", end="")
            print()

but there is a catch because it is almost impossible to return a pattern so we have to print instead of return it then use it directly oddOrEven(5) will print:

 * * * * *
  * * * *
   * * *
    * *
     *

Answer 19

Determining even/odd:

is_odd = num & 1

is_even = (num & 1) == 0  # slowly: bitwise and number comparison 
is_even = (num & 1) is 0  # faster: bitwise and pointer comparsion
is_even = ~num & 1        # fastest: two bitwise operations

Using is is faster than the comparisons with double equals, but negation with ~ is even faster.

Answer 20

There is a simple lambda function that I really like which is:

(lambda x: x % 2 and 'odd' or 'even')