SortedList<>, SortedDictionary<> and Dictionary<>

Question

I find that SortedList<TKey, TValue> SortedDictionary<TKey, TValue> and Dictionary<TKey, TValue> implement the same interfaces.

1. When should we opt for SortedList and SortedDictionary over Dictionary?
2. What is the difference between SortedList and SortedDictionary in terms of application?

Answer 1

1. When iterating over the elements in either of the two, the elements will be sorted. Not so with Dictionary<T,V>.

2. MSDN addresses the difference between SortedList<T,V> and SortedDictionary<T,V>:

The SortedDictionary(TKey, TValue) generic class is a binary search tree with O(log n) retrieval, where n is the number of elements in the dictionary. In this respect, it is similar to the SortedList(TKey, TValue) generic class. The two classes have similar object models, and both have O(log n) retrieval. Where the two classes differ is in memory use and speed of insertion and removal:

SortedList(TKey, TValue) uses less memory than SortedDictionary(TKey, TValue).

SortedDictionary(TKey, TValue) has faster insertion and removal operations for unsorted data: O(log n) as opposed to O(n) for SortedList(TKey, TValue).

If the list is populated all at once from sorted data, SortedList(TKey, TValue) is faster than SortedDictionary(TKey, TValue).

Answer 2

I'd mention difference between dictionaries.

Above picture shows that Dictionary<K,V> is equal or faster in every case than Sorted analog, but if order of elements is required, e.g. to print them, Sorted one is chosen.

Src: http://people.cs.aau.dk/~normark/oop-csharp/html/notes/collections-note-time-complexity-dictionaries.html

Answer 3

To summarize the results of a Performance Test - SortedList vs. SortedDictionary vs. Dictionary vs. Hashtable, the results from best to worst for different scenarios:

Memory Usage:

SortedList<T,T>
Hashtable
SortedDictionary<T,T>
Dictionary<T,T>

Insertions:

Dictionary<T,T>
Hashtable
SortedDictionary<T,T>
SortedList<T,T>

Search Operations:

Hashtable
Dictionary<T,T>
SortedList<T,T>
SortedDictionary<T,T>

foreach loop operations

SortedList<T,T>
Dictionary<T,T>
Hashtable
SortedDictionary<T,T>

Answer 4

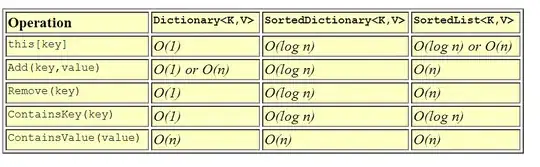
I can see the proposed answers focus on performance. The article provided below does not provide anything new regarding performance, but it explains the underlying mechanisms. Also note it does not focus on the three Collection Types mentioned in the question, but addresses all the Types of the System.Collections.Generic namespace.

http://geekswithblogs.net/BlackRabbitCoder/archive/2011/06/16/c.net-fundamentals-choosing-the-right-collection-class.aspx

Extracts:

Dictionary<>

The Dictionary is probably the most used associative container class. The Dictionary is the fastest class for associative lookups/inserts/deletes because it uses a hash table under the covers. Because the keys are hashed, the key type should correctly implement GetHashCode() and Equals() appropriately or you should provide an external IEqualityComparer to the dictionary on construction. The insert/delete/lookup time of items in the dictionary is amortized constant time - O(1) - which means no matter how big the dictionary gets, the time it takes to find something remains relatively constant. This is highly desirable for high-speed lookups. The only downside is that the dictionary, by nature of using a hash table, is unordered, so you cannot easily traverse the items in a Dictionary in order.

SortedDictionary<>

The SortedDictionary is similar to the Dictionary in usage but very different in implementation. The SortedDictionary uses a binary tree under the covers to maintain the items in order by the key. As a consequence of sorting, the type used for the key must correctly implement IComparable so that the keys can be correctly sorted. The sorted dictionary trades a little bit of lookup time for the ability to maintain the items in order, thus insert/delete/lookup times in a sorted dictionary are logarithmic - O(log n). Generally speaking, with logarithmic time, you can double the size of the collection and it only has to perform one extra comparison to find the item. Use the SortedDictionary when you want fast lookups but also want to be able to maintain the collection in order by the key.

SortedList<>

The SortedList is the other sorted associative container class in the generic containers. Once again SortedList, like SortedDictionary, uses a key to sort key-value pairs. Unlike SortedDictionary, however, items in a SortedList are stored as sorted array of items. This means that insertions and deletions are linear - O(n) - because deleting or adding an item may involve shifting all items up or down in the list. Lookup time, however is O(log n) because the SortedList can use a binary search to find any item in the list by its key. So why would you ever want to do this? Well, the answer is that if you are going to load the SortedList up-front, the insertions will be slower, but because array indexing is faster than following object links, lookups are marginally faster than a SortedDictionary. Once again I'd use this in situations where you want fast lookups and want to maintain the collection in order by the key, and where insertions and deletions are rare.

---

Tentative Summary of underlying Procedures

Feedback is very welcome as I am sure I did not get everything right.

• All arrays are of size n.
• Non-sorted array = .Add/.Remove is O(1), but .Item(i) is O(n).
• Sorted array = .Add/.Remove is O(n), but .Item(i) is O(log n).

Dictionary

Memory

KeyArray(n) -> non-sorted array<pointer>
ItemArray(n) -> non-sorted array<pointer>
HashArray(n) -> sorted array<hashvalue>

Add

1. Add HashArray(n) = Key.GetHash # O(1)
2. Add KeyArray(n) = PointerToKey # O(1)
3. Add ItemArray(n) = PointerToItem # O(1)

Remove

1. For i = 0 to n, find i where HashArray(i) = Key.GetHash # O(log n) (sorted array)
2. Remove HashArray(i) # O(n) (sorted array)
3. Remove KeyArray(i) # O(1)
4. Remove ItemArray(i) # O(1)

Get Item

1. For i = 0 to n, find i where HashArray(i) = Key.GetHash # O(log n) (sorted array)
2. Return ItemArray(i)

Loop Through

1. For i = 0 to n, return ItemArray(i)

SortedDictionary

Memory

KeyArray(n) = non-sorted array<pointer>
ItemArray(n) = non-sorted array<pointer>
OrderArray(n) = sorted array<pointer>

Add

1. Add KeyArray(n) = PointerToKey # O(1)
2. Add ItemArray(n) = PointerToItem # O(1)
3. For i = 0 to n, find i where KeyArray(i-1) < Key < KeyArray(i) (using ICompare) # O(n)
4. Add OrderArray(i) = n # O(n) (sorted array)

Remove

1. For i = 0 to n, find i where KeyArray(i).GetHash = Key.GetHash # O(n)
2. Remove KeyArray(SortArray(i)) # O(n)
3. Remove ItemArray(SortArray(i)) # O(n)
4. Remove OrderArray(i) # O(n) (sorted array)

Get Item

1. For i = 0 to n, find i where KeyArray(i).GetHash = Key.GetHash # O(n)
2. Return ItemArray(i)

Loop Through

1. For i = 0 to n, return ItemArray(OrderArray(i))

SortedList

Memory

KeyArray(n) = sorted array<pointer>
ItemArray(n) = sorted array<pointer>

Add

1. For i = 0 to n, find i where KeyArray(i-1) < Key < KeyArray(i) (using ICompare) # O(log n)
2. Add KeyArray(i) = PointerToKey # O(n)
3. Add ItemArray(i) = PointerToItem # O(n)

Remove

1. For i = 0 to n, find i where KeyArray(i).GetHash = Key.GetHash # O(log n)
2. Remove KeyArray(i) # O(n)
3. Remove ItemArray(i) # O(n)

Get Item

1. For i = 0 to n, find i where KeyArray(i).GetHash = Key.GetHash # O(log n)
2. Return ItemArray(i)

Loop Through

1. For i = 0 to n, return ItemArray(i)

Answer 5

1. When you want the collection to be sorted by key when you iterate over it. If you don't need your data to be sorted, you're better off with just a Dictionary, it'll have better performance.

2. SortedList and SortedDictionary pretty much do the same thing, but are implemented differently, thus have different strengths and weaknesses explained here.

Answer 6

Trying to assign a performance score to each case presented by @Lev, I used the following values:

• O(1) = 3
• O(log n) = 2
• O(n) = 1
• O(1) or O(n) = 2
• O(log n) or O(n) = 1.5

The results are (higher = better):

Dictionary:       12.0 
SortedDictionary:  9.0 
SortedList:        6.5

Of course, every use-case will give more weight to certain operations.