What's the difference between SortedList and SortedDictionary?

Question

Is there any real practical difference between a SortedList<TKey,TValue> and a SortedDictionary<TKey,TValue>? Are there any circumstances where you would specifically use one and not the other?

Answer 1

Yes - their performance characteristics differ significantly. It would probably be better to call them SortedList and SortedTree as that reflects the implementation more closely.

Look at the MSDN docs for each of them (SortedList, SortedDictionary) for details of the performance for different operations in different situtations. Here's a nice summary (from the SortedDictionary docs):

The SortedDictionary<TKey, TValue> generic class is a binary search tree with O(log n) retrieval, where n is the number of elements in the dictionary. In this, it is similar to the SortedList<TKey, TValue> generic class. The two classes have similar object models, and both have O(log n) retrieval. Where the two classes differ is in memory use and speed of insertion and removal:

• SortedList<TKey, TValue> uses less memory than SortedDictionary<TKey, TValue>.

• SortedDictionary<TKey, TValue> has faster insertion and removal operations for unsorted data, O(log n) as opposed to O(n) for SortedList<TKey, TValue>.

• If the list is populated all at once from sorted data, SortedList<TKey, TValue> is faster than SortedDictionary<TKey, TValue>.

(SortedList actually maintains a sorted array, rather than using a tree. It still uses binary search to find elements.)

Answer 2

Here is a tabular view if it helps...

From a performance perspective:

+------------------+---------+----------+--------+----------+----------+---------+
| Collection       | Indexed | Keyed    | Value  | Addition |  Removal | Memory  |
|                  | lookup  | lookup   | lookup |          |          |         |
+------------------+---------+----------+--------+----------+----------+---------+
| SortedList       | O(1)    | O(log n) | O(n)   | O(n)*    | O(n)     | Lesser  |
| SortedDictionary | O(n)**  | O(log n) | O(n)   | O(log n) | O(log n) | Greater |
+------------------+---------+----------+--------+----------+----------+---------+

  * Insertion is O(log n) for data that are already in sort order, so that each 
    element is added to the end of the list. If a resize is required, that element
    takes O(n) time, but inserting n elements is still amortized O(n log n).
    list.
** Available through enumeration, e.g. Enumerable.ElementAt.

From an implementation perspective:

+------------+---------------+----------+------------+------------+------------------+
| Underlying | Lookup        | Ordering | Contiguous | Data       | Exposes Key &    |
| structure  | strategy      |          | storage    | access     | Value collection |
+------------+---------------+----------+------------+------------+------------------+
| 2 arrays   | Binary search | Sorted   | Yes        | Key, Index | Yes              |
| BST        | Binary search | Sorted   | No         | Key        | Yes              |
+------------+---------------+----------+------------+------------+------------------+

To roughly paraphrase, if you require raw performance SortedDictionary could be a better choice. If you require lesser memory overhead and indexed retrieval SortedList fits better. See this question for more on when to use which.

You can read more here, here, here, here and here.

Answer 3

I cracked open Reflector to have a look at this as there seems to be a bit of confusion about SortedList. It is in fact not a binary search tree, it is a sorted (by key) array of key-value pairs. There is also a TKey[] keys variable which is sorted in sync with the key-value pairs and used to binary search.

Here is some source (targeting .NET 4.5) to backup my claims.

Private members

// Fields
private const int _defaultCapacity = 4;
private int _size;
[NonSerialized]
private object _syncRoot;
private IComparer<TKey> comparer;
private static TKey[] emptyKeys;
private static TValue[] emptyValues;
private KeyList<TKey, TValue> keyList;
private TKey[] keys;
private const int MaxArrayLength = 0x7fefffff;
private ValueList<TKey, TValue> valueList;
private TValue[] values;
private int version;

SortedList.ctor(IDictionary, IComparer)

public SortedList(IDictionary<TKey, TValue> dictionary, IComparer<TKey> comparer) : this((dictionary != null) ? dictionary.Count : 0, comparer)
{
    if (dictionary == null)
    {
        ThrowHelper.ThrowArgumentNullException(ExceptionArgument.dictionary);
    }
    dictionary.Keys.CopyTo(this.keys, 0);
    dictionary.Values.CopyTo(this.values, 0);
    Array.Sort<TKey, TValue>(this.keys, this.values, comparer);
    this._size = dictionary.Count;
}

SortedList.Add(TKey, TValue) : void

public void Add(TKey key, TValue value)
{
    if (key == null)
    {
        ThrowHelper.ThrowArgumentNullException(ExceptionArgument.key);
    }
    int num = Array.BinarySearch<TKey>(this.keys, 0, this._size, key, this.comparer);
    if (num >= 0)
    {
        ThrowHelper.ThrowArgumentException(ExceptionResource.Argument_AddingDuplicate);
    }
    this.Insert(~num, key, value);
}

SortedList.RemoveAt(int) : void

public void RemoveAt(int index)
{
    if ((index < 0) || (index >= this._size))
    {
        ThrowHelper.ThrowArgumentOutOfRangeException(ExceptionArgument.index, ExceptionResource.ArgumentOutOfRange_Index);
    }
    this._size--;
    if (index < this._size)
    {
        Array.Copy(this.keys, index + 1, this.keys, index, this._size - index);
        Array.Copy(this.values, index + 1, this.values, index, this._size - index);
    }
    this.keys[this._size] = default(TKey);
    this.values[this._size] = default(TValue);
    this.version++;
}

Answer 4

Enough is said already on the topic, however to keep it simple, here's my take.

Sorted dictionary should be used when-

• More inserts and delete operations are required.
• Data in un-ordered.
• Key access is enough and index access is not required.
• Memory is not a bottleneck.

On the other side, Sorted List should be used when-

• More lookups and less inserts and delete operations are required.
• Data is already sorted (if not all, most).
• Index access is required.
• Memory is an overhead.

Hope this helps!!

Answer 5

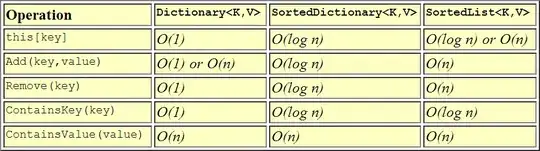
This is visual representation of how performances compare to each other.

Answer 6

Check out the MSDN page for SortedList:

From Remarks section:

The SortedList<(Of <(TKey, TValue>)>) generic class is a binary search tree with O(log n) retrieval, where n is the number of elements in the dictionary. In this, it is similar to the SortedDictionary<(Of <(TKey, TValue>)>) generic class. The two classes have similar object models, and both have O(log n) retrieval. Where the two classes differ is in memory use and speed of insertion and removal:

• SortedList<(Of <(TKey, TValue>)>) uses less memory than SortedDictionary<(Of <(TKey, TValue>)>).

• SortedDictionary<(Of <(TKey, TValue>)>) has faster insertion and removal operations for unsorted data, O(log n) as opposed to O(n) for SortedList<(Of <(TKey, TValue>)>).

• If the list is populated all at once from sorted data, SortedList<(Of <(TKey, TValue>)>) is faster than SortedDictionary<(Of <(TKey, TValue>)>).

Answer 7

Index access (mentioned here) is the practical difference. If you need to access the successor or predecessor, you need SortedList. SortedDictionary cannot do that so you are fairly limited with how you can use the sorting (first / foreach).