Matrix needed to convert rotations for one coordinate system to another

Question

i have rotationmatrixes in a "selfmade" GL coordinate system, and want to apply them to a collada coordinate system.

I know i need a Matrix to multiply the GL rotations to convert them into the collada coordinate system ( where Z is actually UP). The coordinate systems are shown in the picture here :

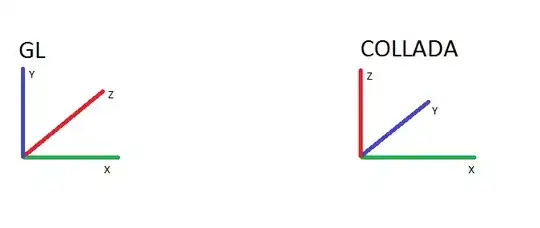
enter image description here

i need the conversion from the left system to the right..for more understanding:
ColladaMatrix=GLRotMatrix*NeededMatrix

Does someone know the matrix i need?

What you are asking for cannot be done with a rotation matrix, because a rotation preserves the handedness of the system and the two systems you shoẁ are of different handedness. Also note that in GL the z axis is oriented in opposite direction as in your image. — Nobody moving away from SE, Apr 03 '13 at 13:02
The GL coordinate system provided here is used by a framework created by one of my coworkers — Captain GouLash, Apr 03 '13 at 13:08

Dr_Sam · Accepted Answer · 2013-04-03T15:26:11.957

5

I think that you need to multiply by two matrices to change the basis of your rotation matrix.

Indeed, the ColladaMatrix is the one that does ([col] mean in the collada coordinates, [gl] in the GL coordinates)

y[col] = R[col,col] x[col]

but if you want to use the GL matrix, you need to transform the x[col] into GL coordinates, then apply the rotation in the GL basis and finally come back to the Collada coordinates. So

y[col] = B[gl->col] R[gl,gl] B[col->gl] x[col]

So,

R[col,col] = B[gl->col] R[gl,gl] B[col->gl]

and here B[gl->col] and B[col->gl] are the same, so

                  [1 0 0                  [1 0 0
MatrixCollada  =   0 0 1   * MatrixGL *    0 0 1
                   0 1 0]                  0 1 0]

Hope it helps!

Remark: The same happen when diagonalizing a matrix (which is actually a change of basis), you need to pre- and post-multiply the matrix that you want to diagonalize.

Edit: I wrote the two coordinates systems for the matrices, because in general, a matrix can send a vector from a coordinate system to another one. This makes it more clear.

edited Apr 03 '13 at 15:26

answered Apr 03 '13 at 13:20

Dr_Sam

1,818
18
24

Before i rotate/translate i get the rotationmatrix, then get the point(vector) of the joint i want to move..after that i convert it to a complete transformation matrix(4x4)..finally i apply them to the node..so basically what i have to do is " convertmatrix * rotationmatrix * convertmatrix " then get the vector and then convert it to the transformationmatrix? – Captain GouLash Apr 03 '13 at 13:52
1

@CaptainGouLash: Just try to remember the coordinate system your data is currently in. Lets say you start with COLLADA coordinates data. Then you apply the conversion matrix and your data is in "GL" coordinates. Then you can apply your GL transformations. When you are done you apply the conversion matrix and are back in COLLADA coordinates. – Nobody moving away from SE Apr 03 '13 at 14:20
I assumed that you have your point starting point x (that you want to move) is in the collada coordinates, that you want the result in the collada coordinates, but that the matrix is in the GL coordinates. To move you point, you need to (1) transform it from collada to GL (2) transform it in GL coordinates (3) transform the result back from GL to collada. The operation (1) is the matrix B[col->gl], operation (2) the MatrixGL and operation (3) the matrix B(gl->col). – Dr_Sam Apr 03 '13 at 14:31
its ALMOST right..could you/someone explain me this matrix? one axis is still weird.. the other ones are good to go! Up and down works fine. but when i move my arm forward, the model moves backwards – Captain GouLash Apr 04 '13 at 08:22
Which axis exactly does not work? y? Are you sure that your graphic is right then? You can try to put -1 instead of 1 in both (#) the element (2,3) of the matrix on the left (#) the element (3,2) of the matrix on the right. – Dr_Sam Apr 04 '13 at 09:38

score 0 · Answer 2 · answered Apr 03 '13 at 13:20

I see, that I misread the part about rotation matrices in your question. I thought you were asking for the rotation matrix, that would convert the GL coordinates into COLLODA coordinates.

These are the matrices that will convert the left system (the one you labeled "GL") to the right system ("COLLADA"):

1 0 0
0 0 1
0 1 0

to convert the other way around you would use the same matrix.

JP Cordova · Answer 3 · 2013-04-03T16:32:16.010

0

DirectX and many libraries and game engines (not OpenGL) work with left hand rule system, and almost all mathematics models and devices that you will find work with right hand rule, this referred to math cross product of vectors.

That's why there is no possible to convert one system to another throw simple rotations.

You must choose one coord system to work, try to use that will use most, and then make some useful functions to convert to one coord system to another.

For experience I can tell you that quaternions are the best way to void this problems, choosing the correct matrix taking on count the hand system of destiny.

If you have problems with rotation (and you will if you use pitch over 90°), search for gimbal lock, and then use quaternions, that will save a lot of time and effort.

Then look this : Euler to Quaternion, and change sin(x) by -sin(x) to change between one coord system to another.

best regards.

edited Apr 03 '13 at 16:32

answered Apr 03 '13 at 15:11

JP Cordova

119
9

I am having troubles to understand what you want to say sometimes, but let me note something: [OpenGL uses a right handed system](http://stackoverflow.com/a/12336360/760746). Also I think you misunderstood the OP in the same way as I did. He did not ask for a rotation matrix that will convert between the coordinate systems of GL and COLLADA. – Nobody moving away from SE Apr 03 '13 at 15:53
That I try to say with all this is that rotation is a "point of view problem", everything is relative from the point of view you use to model the rotation to another observer with a different model of rotations. And you need to "translate" the problem to your point of view to work properly with it. The only way I know to void this "translation" problems are with quaternions, but, is a bit complex to understand at beginning. – JP Cordova Apr 03 '13 at 16:45

Matrix needed to convert rotations for one coordinate system to another

3 Answers3