autocurve.edges does an amazing job of curving edges in igraph plots so that they don't overlap when they point in the same direction. However, when they point in opposite directions, no curvature is applied.
d <- data.frame(start=c("a","a","b","c"),end=c("b","b","c","b"))
graph <- graph.data.frame(d, directed=T)
plot(graph,
vertex.color="white")
The issue is for the arrows between b and c (or c and b).
Other than specifying curvature manually, any suggestions?
I would use the edge.curved option with the same seq call that autocurve.edges uses.
plot(graph,
vertex.color="white", edge.curved=seq(-0.5, 0.5, length = ecount(graph)))
As Étienne pointed out, this solution also curves edges for unique observations. The solution is then to modify the autocurve.edges function. This is my modified function called autocurve.edges2. Basically, it generates a vector, which curves only non-unique edges.
autocurve.edges2 <-function (graph, start = 0.5)
{
cm <- count.multiple(graph)
mut <-is.mutual(graph) #are connections mutual?
el <- apply(get.edgelist(graph, names = FALSE), 1, paste,
collapse = ":")
ord <- order(el)
res <- numeric(length(ord))
p <- 1
while (p <= length(res)) {
m <- cm[ord[p]]
mut.obs <-mut[ord[p]] #are the connections mutual for this point?
idx <- p:(p + m - 1)
if (m == 1 & mut.obs==FALSE) { #no mutual conn = no curve
r <- 0
}
else {
r <- seq(-start, start, length = m)
}
res[ord[idx]] <- r
p <- p + m
}
res
}
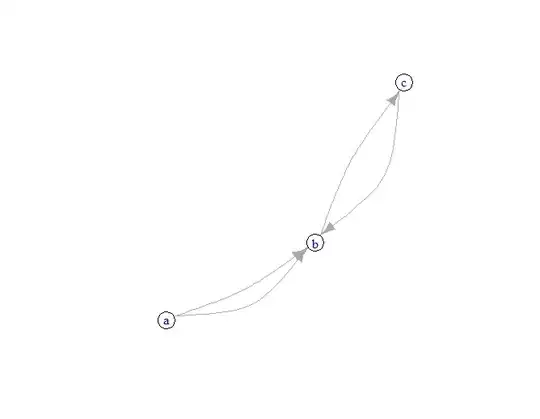
And here's the result when adding a single, non-mutual edge (C->D):
library(igraph)
d <- data.frame(start=c("a","a","b","c","c"),end=c("b","b","c","b","d"))
graph <- graph.data.frame(d, directed=T)
curves <-autocurve.edges2(graph)
plot(graph, vertex.color="white", edge.curved=curves)
