4

In implementing Blinn/Loop's algorithm on curve rendering, I realize there is a special case on Loop Curve Type. As described in their paper (subsection 4.4, page 6-7), they said the curve should be divided into two but I'm really confused how to obtain the intersection point.

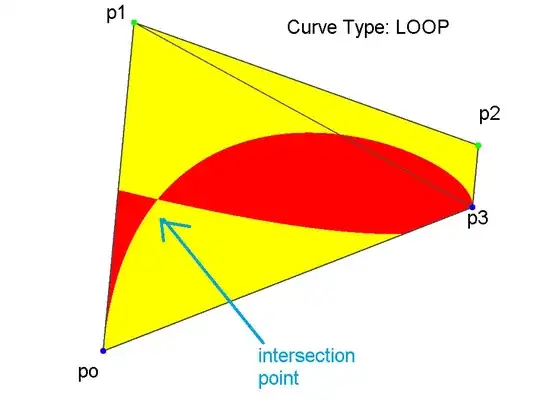
Here's my rendering result: enter image description here

As stated in the paper, this artifact occurs when either td/sd or te/se lie in between value [0, 1].

My source code:

    ...

case CURVE_TYPE_LOOP:

    td = d2 + sqrt(4.0 * d1 * d3 - 3.0 * d2 *d2);
    sd = 2.0 * d1;

    te = d2 - sqrt(4.0 * d1 * d3 - 3.0 * d2 * d2);
    se = 2.0 * d1;

    if((td / sd > 0.0 && td/ sd < 1.0) || (te / se > 0.0 && te/ se < 1.0))
        std::cout << "error\n";

    // F matrix will be multiplied with inverse M3 to obtain tex coords (I use Eigen library btw...)
    F << td * te,                   td * td * te,                               td * te * te,                           1,      
         (-se * td) - (se * te),    (-se * td * td) - (2.0 * sd * te * td),     (-sd * te * te) - (2.0 * se * td * te), 0,
         sd * se,                   te * sd * sd + 2.0 * se * td* sd,           td * se * se + 2 * sd * te * se,        0,
         0,                         -sd * sd * se,                              -sd * se * se,                          0;

    break;

...
genpfault
  • 51,148
  • 11
  • 85
  • 139
azer89
  • 1,529
  • 1
  • 15
  • 29

1 Answers1

5

Solved it,

I should get the splitting value t,

here's my code:

// get t
double splitLoop = -1.0;

switch (curve_type)
{

case CURVE_TYPE_UNKNOWN:
    break;

case CURVE_TYPE_SERPENTINE:

    tl = d2 + ((1.0 / sqrt(3.0)) * sqrt(3.0 * d2 * d2 - 4.0 * d1 * d3));
    sl = 2.0 * d1;

    tm = d2 - ((1.0 / sqrt(3.0)) * sqrt(3.0 * d2 * d2 - 4.0 * d1 * d3));
    sm = 2.0 * d1;

    F << tl * tm,                   tl * tl * tl,           tm * tm * tm,           1,
        -(sm * tl) -(sl * tm),      -(3.0 * sl * tl * tl),  -(3.0 * sm * tm * tm),  0,
        sl * sm,                    3.0 * sl * sl * tl,     3.0 * sm * sm *  tm,    0,
        0,                          -(sl * sl * sl),        -(sm * sm * sm),        0;  

    break;

case CURVE_TYPE_LOOP:

    td = d2 + sqrt(4.0 * d1 * d3 - 3.0 * d2 *d2);
    sd = 2.0 * d1;

    te = d2 - sqrt(4.0 * d1 * d3 - 3.0 * d2 * d2);
    se = 2.0 * d1;

    // Get splitting t
    if((td / sd) > 0.0 && (td / sd) < 1.0)
    {
        splitLoop = td / sd;
    }
    else if((te / se) > 0.0 && (te/ se) < 1.0)
    {
        splitLoop = te / se;
    }

    F << td * te,                   td * td * te,                               td * te * te,                           1,      
            (-se * td) - (se * te), (-se * td * td) - (2.0 * sd * te * td),     (-sd * te * te) - (2.0 * se * td * te), 0,
            sd * se,                te * sd * sd + 2.0 * se * td* sd,           td * se * se + 2 * sd * te * se,        0,
            0,                      -sd * sd * se,                              -sd * se * se,                          0;

    break;

case CURVE_TYPE_QUADRATIC:
    break;

case CURVE_TYPE_LINE:
    break;

}

if(splitLoop > 0.0 && splitLoop < 1.0)
{
    // SPLIT
    double x01 = (x1 - x0) * splitLoop + x0;
    double y01 = (y1 - y0) * splitLoop + y0;

    double x12 = (x2 - x1) * splitLoop + x1;
    double y12 = (y2 - y1) * splitLoop + y1;

    double x23 = (x3 - x2) * splitLoop + x2;
    double y23 = (y3 - y2) * splitLoop + y2;

    double x012 = (x12 - x01) * splitLoop + x01;
    double y012 = (y12 - y01) * splitLoop + y01;

    double x123 = (x23 - x12) * splitLoop + x12;
    double y123 = (y23 - y12) * splitLoop + y12;

    double x0123 = (x123 - x012) * splitLoop + x012;
    double y0123 = (y123 - y012) * splitLoop + y012;

    // CURVE A (recursive)
    DrawCubic(x0, y0, x01, y01, x012, y012, x0123, y0123);

    // CURVE B (recursive)
    DrawCubic(x0123,  y0123, x123, y123, x23, y23, x3, y3);
}
else
{
    // Draw as usual...

}

== EDIT ==

After i experimented again for a while, There's a numerical error on my program when the values of td/sd or te/se on subcurves lie again in between [0, 1], since my program use recursive by calling DrawCubic(), it causes recursive heap error.

In the meantime, I use 'hack' solution where I will not call DrawCurve() inside the recursive call (making sure the recursive is called only once). So far the result is quite satisfying and I don't see any artifact.

Any feedback is really welcomed since I'm not really good in numerical calculation :)

enter image description here

azer89
  • 1,529
  • 1
  • 15
  • 29