6

UPDATES

  • My original implementation in C#
  • My final implementation in C#, based on the answers I got.

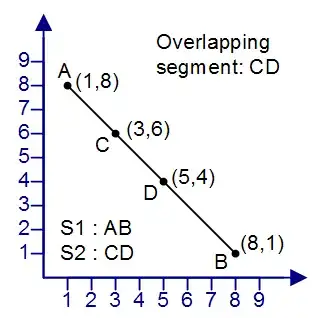
Given the following conditions, how can I programatically find the overlapping segment between two lines?

Also, for a different slope:

And for vertical lines:

And for horizontal lines:

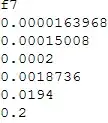
Note: For all the quadrants !

I've started by coding all possible conditions but it gets ugly.

public Line GetOverlap (Line line1, Line line2)
{
    double line1X1 = line1.X1;
    double line1Y1 = line1.Y1;
    double line1X2 = line1.X2;
    double line1Y2 = line1.Y2;
    double line2X1 = line2.X1;
    double line2Y1 = line2.Y1;
    double line2X2 = line2.X2;
    double line2Y2 = line2.Y2;

    if (line1X1 > line1X2)
    {
        double swap = line1X1;
        line1X1 = line1X2;
        line1X2 = swap;

        swap = line1Y1;
        line1Y1 = line1Y2;
        line1Y2 = swap;
    }
    else if (line1X1.AlmostEqualTo (line1X2))
    {
        if (line1Y1 > line1Y2)
        {
            double swap = line1Y1;
            line1Y1 = line1Y2;
            line1Y2 = swap;

            swap = line1X1;
            line1X1 = line1X2;
            line1X2 = swap;
        }
    }

    if (line2X1 > line2X2)
    {
        double swap = line2X1;
        line2X1 = line2X2;
        line2X2 = swap;

        swap = line2Y1;
        line2Y1 = line2Y2;
        line2Y2 = swap;
    }
    else if (line2X1.AlmostEqualTo (line2X2))
    {
        if (line2Y1 > line2Y2)
        {
            double swap = line2Y1;
            line2Y1 = line2Y2;
            line2Y2 = swap;

            swap = line2X1;
            line2X1 = line2X2;
            line2X2 = swap;
        }
    }

    double line1MinX = Math.Min (line1X1, line1X2);
    double line2MinX = Math.Min (line2X1, line2X2);
    double line1MinY = Math.Min (line1Y1, line1Y2);
    double line2MinY = Math.Min (line2Y1, line2Y2);
    double line1MaxX = Math.Max (line1X1, line1X2);
    double line2MaxX = Math.Max (line2X1, line2X2);
    double line1MaxY = Math.Max (line1Y1, line1Y2);
    double line2MaxY = Math.Max (line2Y1, line2Y2);

    double overlap;
    if (line1MinX < line2MinX)
        overlap = Math.Max (line1X1, line1X2) - line2MinX;
    else
        overlap = Math.Max (line2X1, line2X2) - line1MinX;

    if (overlap <= 0)
        return null;

    double x1;
    double y1;
    double x2;
    double y2;

    if (line1MinX.AlmostEqualTo (line2MinX))
    {
        x1 = line1X1;
        x2 = x1;
        y1 = line1MinY < line2MinY
                 ? line2Y1
                 : line1Y1;
        y2 = line1MaxY < line2MaxY
                 ? line1Y2
                 : line2Y2;
    }
    else
    {
        if (line1MinX < line2MinX)
        {
            x1 = line2X1;
            y1 = line2Y1;
        }
        else
        {
            x1 = line1X1;
            y1 = line1Y1;
        }

        if (line1MaxX > line2MaxX)
        {
            x2 = line2X2;
            y2 = line2Y2;
        }
        else
        {
            x2 = line1X2;
            y2 = line1Y2;
        }
    }

    return new Line (x1, y1, x2, y2);
}

I'm sure an algorithm exists for this but I was unable to find one on the web.

UPDATE with solution based on answers I got:

This solution account for all the cases I could think of (verticals, horizontals, positive slope, negative slope, not intersecting)

public Line GetOverlap (Line line1, Line line2)
{
    double slope = (line1.Y2 - line1.Y1)/(line1.X2 - line1.X1);
    bool isHorizontal = AlmostZero (slope);
    bool isDescending = slope < 0 && !isHorizontal;
    double invertY = isDescending || isHorizontal ? -1 : 1;

    Point min1 = new Point (Math.Min (line1.X1, line1.X2), Math.Min (line1.Y1*invertY, line1.Y2*invertY));
    Point max1 = new Point (Math.Max (line1.X1, line1.X2), Math.Max (line1.Y1*invertY, line1.Y2*invertY));

    Point min2 = new Point (Math.Min (line2.X1, line2.X2), Math.Min (line2.Y1*invertY, line2.Y2*invertY));
    Point max2 = new Point (Math.Max (line2.X1, line2.X2), Math.Max (line2.Y1*invertY, line2.Y2*invertY));

    Point minIntersection;
    if (isDescending)
        minIntersection = new Point (Math.Max (min1.X, min2.X), Math.Min (min1.Y*invertY, min2.Y*invertY));
    else
        minIntersection = new Point (Math.Max (min1.X, min2.X), Math.Max (min1.Y*invertY, min2.Y*invertY));

    Point maxIntersection;
    if (isDescending)
        maxIntersection = new Point (Math.Min (max1.X, max2.X), Math.Max (max1.Y*invertY, max2.Y*invertY));
    else
        maxIntersection = new Point (Math.Min (max1.X, max2.X), Math.Min (max1.Y*invertY, max2.Y*invertY));

    bool intersect = minIntersection.X <= maxIntersection.X && 
                     (!isDescending && minIntersection.Y <= maxIntersection.Y ||
                       isDescending && minIntersection.Y >= maxIntersection.Y);

    if (!intersect)
        return null;

    return new Line (minIntersection, maxIntersection);
}

public bool AlmostEqualTo (double value1, double value2)
{
    return Math.Abs (value1 - value2) <= 0.00001;
}

public bool AlmostZero (double value)
{
    return Math.Abs (value) <= 0.00001;
}
user3731528
  • 333
  • 1
  • 2
  • 9
Stécy
  • 11,951
  • 16
  • 64
  • 89
  • What do you mean by "gets ugly?" As it stands this question is very broad; you'd be better off posting some code and asking for more specific help. Why do you need "separate conditions" (I assume for each of your diagrams)? It should be relatively simple to order the points and return the middle two... – Dan Puzey Mar 17 '14 at 14:17
  • What have you tried so far? This is basic vector math. What may be an issue are rounding errors and FP precision. – Ondrej Tucny Mar 17 '14 at 14:21
  • 1
    such complicated answers to a simple problem. Compute length of two segments. lexicographically sort the *points*. If overall length (min-max) > sum of two seg lengths : no overlap, otherwise middle two points are the overlap. If you know a-priori they are colinear you are done, else do the cross product check. – agentp Jun 12 '14 at 15:55

5 Answers5

7

This problem is roughly equivalent to the test whether two axis-aligned rectangles intersect: you can threat every segment as the diagonal of an axis-aligned rectangle, then you need to find the intersection of these two rectangles. The following is the approach I use for rectangle intersection.

Let's assume that the slope of the segments is ascending, vertical, or horizontal; if the segments are descending, negate every y-coordinate so that they are ascending.

Define the MinPoint and MaxPoint for each line segment:

Point min1 = new Point(Math.Min(line1.X1, line1.X2),Math.Min(line1.Y1,line1.Y2);
Point max1 = new Point(Math.Max(line1.X1, line1.X2),Math.Max(line1.Y1,line1.Y2);

Point min2 = new Point(Math.Min(line2.X1, line2.X2),Math.Min(line2.Y1,line2.Y2);
Point max2 = new Point(Math.Max(line2.X1, line2.X2),Math.Max(line2.Y1,line2.Y2);

Now the intersection is given by the following two points: the maximum of the two minimums, and the minimum of the two maximums

Point minIntersection = new Point(Math.Max(min1.X, min2.X), Math.Max(min1.Y, min2.Y));
Point maxIntersection = new Point(Math.Min(max1.X, max2.X), Math.Min(max1.Y, max2.Y));

and that's it. To test whether the two segments intersect at all, you check

bool intersect = (minIntersection.X< maxIntersection.X) && (minIntersection.Y< maxIntersection.Y);

If they do intersect, the intersection is given by the two points minIntersection and maxIntersection. If they do not intersect, the length of the segment (minIntersection, maxIntersection) is the distance between the two original segments.

(If you negated every y-coordinate in the first step, negate the y-coordinate of the result now)

(You can easily extend this approach to cover colinear segments in 3 or more dimensions)

HugoRune
  • 13,157
  • 7
  • 69
  • 144
  • Inverting Y coords for horizontals works but not for descending segments. – Stécy Mar 17 '14 at 17:53
  • sure; if you invert all Y-coordinates for a descending segment, you get an ascending segment; the resulting coordinates are just a mirror image of the originals. – HugoRune Mar 17 '14 at 18:10
  • +1 for not needing a lexicographic sort and yet doing the same thing, even if it requires a little more code. – Nuclearman Mar 19 '14 at 18:12
  • This doesn't work for ascending parallel but not colinear diagonals where the rectangle for line1 intersects with the rectangle for line2 *in the space between the two lines*. The segment calculated is a phantom line halfway between the two line segments. Only use this if the cross product of `min1, max1, max2` is 0. – Martijn Pieters Dec 06 '21 at 16:40
  • The question specified colinear line segments. As far as I recall, this solution does not work for non-colinear line segments, it was originally intended for axis aligned rectangles: the "phantom line" should be the diagonal of the rectangular intersection between two given intersecting rectangles. – HugoRune Dec 06 '21 at 17:21
3

Transform your coordinates so that the line though your segments is the new x-axis.

Sort the points in order from left to right.

If the segments do actually overlap, then the solution will always be the second and third points.

Note: If you aren't guaranteed that the segments overlap, then the test is simple - if the first two points belong to the same segment, then they do not overlap.

mbeckish
  • 10,485
  • 5
  • 30
  • 55
  • If transforming coordinates sounds too scary to attempt, you can also write the equation of your line in [parametric](http://en.wikipedia.org/wiki/Parametric_equation) form, solve for `t` at each point, and sort by `t` instead of sorting "left to right". – mbeckish Mar 17 '14 at 14:30
  • Is it really necessary to "tranform" the coordinates? Could I just sort the points by their X? What about for vertical lines? – Stécy Mar 17 '14 at 14:35
  • @Stécy - See my comment to my answer. You can use the parametric form of the line, and sort by t. If you don't want to do either, then yes you can just sort by x, and deal with the edge case of vertical lines. But you really shouldn't be afraid of coordinate transformations - once you get used to them, they are very easy and powerful. – mbeckish Mar 17 '14 at 14:39
3

You lexicographically sort the two segments, then take the last element of the first segment and first element of the last segment (segments in lexicographical order). This gives you the segment you need.

You can then use the cross-product to determine if they form a line if you want to verify. The 2D cross-product being zero shows that three points form a line.

For example:

B = ((0,0),(3,3))
A = ((2,2),(5,5))

After a lexigraphic sort:

[((0,0),(3,3)),((2,2),(5,5))]
C = ((3,3),(4,4))

You can then check if they overlap by ensuring that the the first element of C is lexigraphically greater than the first element of the second line segment. In the example it is.

And the cross-products for certification of them overlapping. This is done by using the first element of the first list and the last element of the last segment. Then checking each of two elements inner individually to see if they are all in a line via the cross-product of the three points being zero:

cross((0,0),(1,1),(5,5)) = 0
cross((0,0),(4,4),(5,5)) = 0

Therefore the two input segments do form a line.

I'm not familiar enough with C# to ensure correctness, but in Python the algorithm looks like:

def cross(o, a, b):
    return (a[0] - o[0]) * (b[1] - o[1]) - (a[1] - o[1]) * (b[0] - o[0])

def line_segment_overlap(segment_a,segment_b):
    segments = [segment_a.sort(),segment_b.sort()] # 2D Lexicographic sort the line segments
    segments.sort()
    A = segments[0]
    B = segments[1]
    if cross(A[0],A[1],B[1]) == 0 and cross(A[0],B[0],B[1]) == 0: # Segments form a line
        if A[1] > B[0]: # Segments overlap
            return (A[1],B[1]) # New line segment
    return None
Nuclearman
  • 5,029
  • 1
  • 19
  • 35
  • @Stécy: It's a lexicographic sort, it should (although precision might be an issue). If B = ((0,0),(0,2)) and A = ((0,1),(0,4)). Lexicographic sort should yield [((0,0),(0,2)),((0,1),(0,4))]. Are you sorting by x then y if the x values are the same? That's a lexicographic sort. That being said if you are using more than two line segments, then you almost certainly need a more complex algorithm to ensure it gives all the right outputs, but that isn't what your question asks for. – Nuclearman Mar 17 '14 at 14:45
  • Ok, should the result of the sort be (0,0) - (0,1) - (0,2) - (0,4) ? If I sort by X then by Y that would be the result I get. – Stécy Mar 17 '14 at 14:47
  • Oh, and that would not work for non-overlapping segments: (0,0)-(1,1) and (3,3)-(5,5) would give (1,1)-(3,3) and this is not an overlapping segment. – Stécy Mar 17 '14 at 14:53
  • True, but as I pointed out in the answer, it's fairly simple to verify whether or not they overlap. – Nuclearman Mar 17 '14 at 16:17
  • No you need to do a lexicographic sort on the line segments themselves not the end points but that eventually gets down to the points themselves, I only mentioned the X and Y because of what you said the issue was. It'll likely require recursion to compare the first point of the first segment to the first point of the first segment. If those two points are the same, then you compare the second points. I suppose it's easier if you use a language that supports lexicographic sorting rather than trying to implement it yourself. I'm not sure that C# does. – Nuclearman Mar 17 '14 at 16:20
  • I've added a Python implementation to give you an idea of what needs done. Not sure if the C# sort can do that though. – Nuclearman Mar 17 '14 at 16:33
  • I think your Python implementation fails for: ``segment_a = ((3, 0), (0, 0)); segment_b = ((4, 0), (2, 0))`` Lexicographically sorting the points of each segment, then lexicographically sorting the segments, seems to resolve this issue. – Gino Oct 24 '17 at 14:46
  • You are correct. There was an unmentioned assumption of the segment points also being lexicographically sorted, updated the answer. – Nuclearman Oct 25 '17 at 18:09
2

Use the transform that maps the segment AB to (0, 0):(0, 1). Any segment that is collinear with AB will have ordinate 0 for both endpoints, let (c, 0):(d, 0). The overlap is given by (Max(0, c), 0):(Min(1, d), 0), unless Max(0, c) > Min(1, d).

Let ABx = X1 - X0, ABy = Y1 - Y0 and AB^2 = ABx^2 + ABy^2.

x = ((X-XA) ABx + (Y-YA) ABy) / AB^2
y = ((X-XA) ABy - (Y-YA) ABx) / AB^2

If you want the overlap in 2D, apply the inverse transform (with y = 0).

X = XA + x ABx
Y = YA + x ABy
0

I am not 100% sure of this, hopefully the community will tell. I am not posting this as a comment simply because I think that some minor formatting won't hurt.

The way that I see it, the equation of a straight line:

y = mx + c

where

  • y is a given y co-ordinate (in an x-y pair);
  • m is the gradient (slope) of the line;
  • x is a given co-ordinate (the other part of the x-y pair);
  • c is the intercept is key.

For any set of two points, you should be able to compute the equation for the line by:

  1. Finding the value of m (the usual dy/dx)

  2. Find the value of c for y=0.

Once that you will have computed that, you could generate the equation in the form of a string if you will.

Once that you will have gone through all the pairs of points, you should be able to identify line segments that lie on top of each other by checking the equations you have generated. You could then use the co-ordinates of the points on the line to extrapolate 2 rectangles and see which one fits inside the other. This should help you identify which line is within what segment.

npinti
  • 51,780
  • 5
  • 72
  • 96