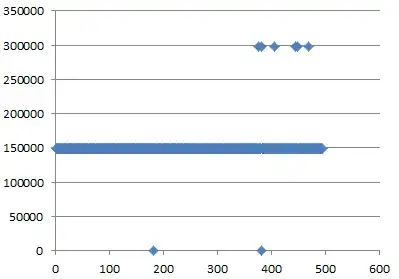
Are there any colormaps or is there a simple way to transform a matplotlib colormap to provide a much bigger color range near 0.5 and a smaller one at the extremes? I am creating a bunch of subplots, one of which has color values of about 10 times the others, so it’s values dominate and the rest of the plots all look the same. For a simple example say we have:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(1,10,10)
y = np.linspace(1,10,10)
t1 = np.random.normal(2,0.3,10)
t2 = np.random.normal(9,0.01,10)
t2_max = max(t2)
plt.figure(figsize=(22.0, 15.50))
p = plt.subplot(1,2,1)
colors = plt.cm.Accent(t1/t2_max)
p.scatter(x, y, edgecolors=colors, s=15, linewidths=4)
p = plt.subplot(1,2,2)
colors = plt.cm.Accent(t2/t2_max)
p.scatter(x, y, edgecolors=colors, s=15, linewidths=4)
plt.subplots_adjust(left=0.2)
cbar_ax = plt.axes([0.10, 0.15, 0.05, 0.7])
sm = plt.cm.ScalarMappable(cmap=plt.cm.Accent, norm=plt.Normalize(vmin=0, vmax=t2_max))
sm._A = []
cbar = plt.colorbar(sm,cax=cbar_ax)
plt.show()
There is much more variation in t1 than in t2, however the variation can not be seen because of the high values of t2. What I want is a map the will provide a larger color gradient around the mean of t1 without transforming the data itself. I have found one solution here http://protracted-matter.blogspot.co.nz/2012/08/nonlinear-colormap-in-matplotlib.html but cant get it to work for my scatter plots.
EDIT: From answer below the class can be modified to take negative numbers, and fixed boundaries.
import numpy as np
import matplotlib.pyplot as plt
x = y = np.linspace(1, 10, 10)
t1mean, t2mean = -6, 9
sigma1, sigma2 = .3, .01
t1 = np.random.normal(t1mean, sigma1, 10)
t2 = np.random.normal(t2mean, sigma2, 10)
class nlcmap(object):
def __init__(self, cmap, levels):
self.cmap = cmap
self.N = cmap.N
self.monochrome = self.cmap.monochrome
self.levels = np.asarray(levels, dtype='float64')
self._x = self.levels
self.levmax = self.levels.max()
self.levmin = self.levels.min()
self.transformed_levels = np.linspace(self.levmin, self.levmax,
len(self.levels))
def __call__(self, xi, alpha=1.0, **kw):
yi = np.interp(xi, self._x, self.transformed_levels)
return self.cmap(yi / (self.levmax-self.levmin)+0.5, alpha)
tmax = 10
tmin = -10
#the choice of the levels depends on the data:
levels = np.concatenate((
[tmin, tmax],
np.linspace(t1mean - 2 * sigma1, t1mean + 2 * sigma1, 5),
np.linspace(t2mean - 2 * sigma2, t2mean + 2 * sigma2, 5),
))
levels = levels[levels <= tmax]
levels.sort()
print levels
cmap_nonlin = nlcmap(plt.cm.jet, levels)
fig, (ax1, ax2) = plt.subplots(1, 2)
ax1.scatter(x, y, edgecolors=cmap_nonlin(t1), s=15, linewidths=4)
ax2.scatter(x, y, edgecolors=cmap_nonlin(t2), s=15, linewidths=4)
fig.subplots_adjust(left=.25)
cbar_ax = fig.add_axes([0.10, 0.15, 0.05, 0.7])
#for the colorbar we map the original colormap, not the nonlinear one:
sm = plt.cm.ScalarMappable(cmap=plt.cm.jet,
norm=plt.Normalize(vmin=tmin, vmax=tmax))
sm._A = []
cbar = fig.colorbar(sm, cax=cbar_ax)
#here we are relabel the linear colorbar ticks to match the nonlinear ticks
cbar.set_ticks(cmap_nonlin.transformed_levels)
cbar.set_ticklabels(["%.2f" % lev for lev in levels])
plt.show()