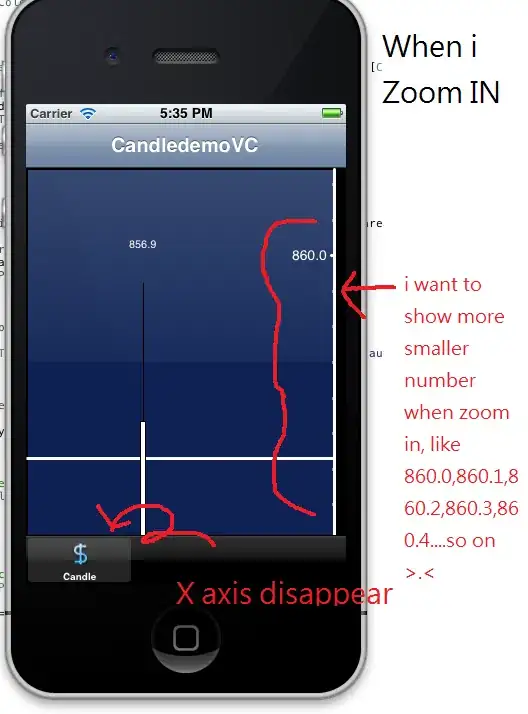
I am working with geographic information, and recently I needed to draw an ellipse. For compatibility with the OGC convention, I cannot use the ellipse as it is; instead, I use an approximation of the ellipse using a polygon, by taking a polygon which is contained by the ellipse and using arbitrarily many points.
The process I used to generate the ellipse for a given number of point N is the following (using C# and a fictional Polygon class):
Polygon CreateEllipsePolygon(Coordinate center, double radiusX, double radiusY, int numberOfPoints)
{
Polygon result = new Polygon();
for (int i=0;i<numberOfPoints;i++)
{
double percentDone = ((double)i)/((double)numberOfPoints);
double currentEllipseAngle = percentDone * 2 * Math.PI;
Point newPoint = CalculatePointOnEllipseForAngle(currentEllipseAngle, center, radiusX, radiusY);
result.Add(newPoint);
}
return result;
}
This has served me quite while so far, but I've noticed a problem with it: if my ellipse is 'stocky', that is, radiusX is much larger than radiusY, the number of points on the top part of the ellipse is the same as the number of points on the left part of the ellipse.
That is a wasteful use of points! Adding a point on the upper part of the ellipse would hardly affect the precision of my polygon approximation, but adding a point to the left part of the ellipse can have a major effect.
What I'd really like, is a better algorithm to approximate the ellipse with a polygon. What I need from this algorithm:
- It must accept the number of points as a parameter; it's OK to accept the number of points in every quadrant (I could iteratively add points in the 'problematic' places, but I need good control on how many points I'm using)
- It must be bounded by the ellipse
- It must contain the points straight above, straight below, straight to the left and straight to the right of the ellipse's center
Its area should be as close as possible to the area of the ellipse, with preference to optimal for the given number of points of course(See Jaan's answer - appearantly this solution is already optimal)- The minimal internal angle in the polygon is maximal
What I've had in mind is finding a polygon in which the angle between every two lines is always the same - but not only I couldn't find out how to produce such a polygon, I'm not even sure one exists, even if I remove the restrictions!
Does anybody have an idea about how I can find such a polygon?