How to generate n different colors for any natural number n?

Question

Say n = 100; How do I generate 100 visually distinct colors? Is this mathematically possible?

Answer 1

Yeah. Defining distinct is a product of deferring to a color space then when we say maximally distinct colors what we mean to say is colors which are as far from all the other colors as possible. But since the color space doesn't change the answer isn't going to change. And implementing something that better fits with human eyes and how human eyes see color like CIE-lab de2000 color distance makes redoing all the calculations hard, but makes a static list easy. Here's 128 entries.

private static final String[] indexcolors = new String[]{
        "#000000", "#FFFF00", "#1CE6FF", "#FF34FF", "#FF4A46", "#008941", "#006FA6", "#A30059",
        "#FFDBE5", "#7A4900", "#0000A6", "#63FFAC", "#B79762", "#004D43", "#8FB0FF", "#997D87",
        "#5A0007", "#809693", "#FEFFE6", "#1B4400", "#4FC601", "#3B5DFF", "#4A3B53", "#FF2F80",
        "#61615A", "#BA0900", "#6B7900", "#00C2A0", "#FFAA92", "#FF90C9", "#B903AA", "#D16100",
        "#DDEFFF", "#000035", "#7B4F4B", "#A1C299", "#300018", "#0AA6D8", "#013349", "#00846F",
        "#372101", "#FFB500", "#C2FFED", "#A079BF", "#CC0744", "#C0B9B2", "#C2FF99", "#001E09",
        "#00489C", "#6F0062", "#0CBD66", "#EEC3FF", "#456D75", "#B77B68", "#7A87A1", "#788D66",
        "#885578", "#FAD09F", "#FF8A9A", "#D157A0", "#BEC459", "#456648", "#0086ED", "#886F4C",
        
        "#34362D", "#B4A8BD", "#00A6AA", "#452C2C", "#636375", "#A3C8C9", "#FF913F", "#938A81",
        "#575329", "#00FECF", "#B05B6F", "#8CD0FF", "#3B9700", "#04F757", "#C8A1A1", "#1E6E00",
        "#7900D7", "#A77500", "#6367A9", "#A05837", "#6B002C", "#772600", "#D790FF", "#9B9700",
        "#549E79", "#FFF69F", "#201625", "#72418F", "#BC23FF", "#99ADC0", "#3A2465", "#922329",
        "#5B4534", "#FDE8DC", "#404E55", "#0089A3", "#CB7E98", "#A4E804", "#324E72", "#6A3A4C",
        "#83AB58", "#001C1E", "#D1F7CE", "#004B28", "#C8D0F6", "#A3A489", "#806C66", "#222800",
        "#BF5650", "#E83000", "#66796D", "#DA007C", "#FF1A59", "#8ADBB4", "#1E0200", "#5B4E51",
        "#C895C5", "#320033", "#FF6832", "#66E1D3", "#CFCDAC", "#D0AC94", "#7ED379", "#012C58"
};

Here's the first 256 as an image.

(left-to-right) (top-to-bottom). You might be able to get a few more distinct colors if you made sure each color was as equidistant as possible within the colorspace. That lookup table picks each additional color as maximally distinct from all previous colors rather than designating the N at the start and then mapping out the colorspace. So yeah, brute force and a high level color distance algorithm and you're set to make this same set of colors yourself. Over the course of a day or so.

---

If you do set lists and make them equidistant you can get a distinct number between different colors for example, , Beats the default list at 5 colors which was at min_delta_max 53.2 with min_delta_max 61.5

Or the colors in the list, , #156FC3 #165859 #24C4FF #30A581 #957D5C #213E02 #DE9AF5 #68D840 #6E0062 #C25B77 which exceeds the first ten elements in the precomputed list.

If you wanted to try this instead: https://gist.github.com/tatarize/a483db49993e6e0e994ad82ba3e2a22e

Can be edited to take num_of_colors, and you can run it for a long time and get a set of colors which should have a lower overall min_delta_max (the biggest maximum minimum distances between any two colors in the list). You'd still want a precompiled list.

Answer 2

Edit:

I don't have any expertise in this area and my math skills are pretty average. But I have the opinion that the solution to this problem is more complex and interesting than many answers here suggest, since I tried to do something similar recently and didn't find a solution.

Color Difference

The perception of color is of course subjective, but there is significant agreement between humans. For example, we can all agree that red, green and blue are very different colors, and even colorblind people agree that black and white are very different.

RGB

The most common representation of color in computer systems is the vector (r, g, b) which suggests a simple distance function like

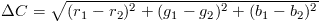
Lets set the range for r, g and b to [0, 1] and see how this works:

1. Red (1, 0, 0) and red (1, 0, 0) has the distance of 0, which should be obvious
2. Red (1, 0, 0) and yellow (1, 1, 0) has the distance of 1, which is smaller than the distance of
3. Red (1, 0, 0) and blue (0, 0, 1) which is sqrt(2), which is plausible

So far, so good. The problem however is that blue and red have the same distance 1 from black (0, 0, 0), but when looking at the image this doesn't seem to hold true:

Also yellow (1, 1, 0) and magenta (1, 0, 1) both have have the same distance 1 from white (1, 1, 1), which doesn't seem to make sense either:

HSL and HSV

I think it is safe to assume that analogue metrics for the HSL and HSV color schemes have the same problems. These color schemes aren't designed for comparing color.

CIEDE2000

Luckily, there are scientists already trying to find a good way to compare colors. They came up with some elaborate methods, the latest one being CIEDE2000

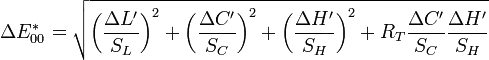
(the full formula described in the article is huge)

This metric takes human perception into consideration, like the fact that we seem to be unable to discern shades of blue very well. So I'd say we use this as our color difference function.

The Color Picking Algorithm

Naive solution

Some answers suggested the following algorithm

colors = []
for n in range(n):
    success=False
    while not success:
        new_color = random_color()
        for color in colors:
            if distance(color, new_color)>far_enough:
                colors.append(new_color)
                success = True
                break

This algorithm has some problems:

1. The spacing of the colors isn't optimal. If we imagine the colors to be like numbers on a line, three numbers would be optimally spaced like this:

   |a-----b-----c|

   Packing an additional one number in there without moving a, b, and c is clearly worse than realigning all the colors.

2. The algorithm isn't guaranteed to terminate. What if there is no color that is far enough form the existing colors in the list? The loop will continue forever

Proper solution

Well.. I don't have one.

Answer 3

100 is a lot of colours, but you might be able to do it by distributing them as sparsely as possible in the HSB or HSL space; doing it in RGB is probably difficult.

For example, you might decide to use 10 different hues, 4 different saturation levels, and 3 different brightness settings, that would give you up to 120 colours. You'll need to pick the saturation and brightness values carefully; human eyes are complicated and confusing sensors. If you treat the colour space as a cone, you will probably want a different number of hues at each lightness/saturation level.

Here's a link to the wikipedia entry on HSB.

Answer 4

You want to convert to HSL and then iterate through the values of the hue (H) while keeping the other 2 values constant.

For each value you convert from HSL back to RGB.

See my answers here and here.

If your N is very large and therefore the colors are NOT visually distinct you could at that point re-iterate over all of the same hues and change the other components to vary the saturation or luminosity. So basically you could have a max number of hue values to use, and once that is hit you can start over with a different saturation or luminosity.

Answer 5

Not an answer to your question, but, if n has a maximum value and your application allows it, you could use a predefined list of colors like this:

http://en.wikipedia.org/wiki/List_of_colors

One advantage is that you could show a humanly readable color name in a tooltip for people with color blindness.

Answer 6

For starters, don't use RGB space; it's hard to find a worse colour space for this problem. (Depending on whether you're using the colours for display or for print you either have huge numbers of indistinguishable colours near black or near white.)

If you use Lab space, there are perceptual colour models (CIE 1996? and CIE 2000) for measuring the visual closeness of colours (for print and display respectively).

You don't say if you're going to compute the colours once and store the result, or if they need to be recomputed on the fly (and in that case if it has to be deterministic or not). Obviously any discussion of how best to generate the set would depend on that.

Though I would suggest that evenly dividing the axes of the colour space (say into 8) and using those as initial points would be much more efficient than any random process. Certainly you only need to compare any point to its neighbours (and only if they're already in the set), which will save you a huge number of comparisons.