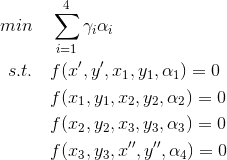Lets say I've a robotic arm with joints at points A,B,C,D in a 3D space. Let D be the end effector(bottommost child) and A be the topmost parent. Let T be the target point anywhere in the space. The aim is to make the end effector reach the target with minimum rotations in top levels(parents).
What I initially thought:
1) Rotate the arm C by angle TCD. 2) Then rotate the arm B by new angle TBD. 3) Then rotate the arm A by new angle TAD.
But the end effector seems to point away from the target after step 2. What am I doing wrong and how can I fix it?