38

I've heard of "error" when using floating point variables. Now I'm trying to solve this puzzle and I think I'm getting some rounding/floating point error. So I'm finally going to figure out the basics of floating point error.

What is a simple example of floating point/rounding error (preferably in C++) ?

Edit: For example say I have an event that has probability p of succeeding. I do this event 10 times (p does not change and all trials are independent). What is the probability of exactly 2 successful trials? I have this coded as:

double p_2x_success = pow(1-p, (double)8) * pow(p, (double)2) * (double)choose(8, 2);

Is this an opportunity for floating point error?

MrDatabase
  • 43,245
  • 41
  • 111
  • 153
  • I think what you really need is this: [What Every Computer Scientist Should Know About Floating-Point Arithmetic](http://docs.sun.com/source/806-3568/ncg_goldberg.html). – Patrick Oct 30 '08 at 07:17
  • Read this: http://blog.frama-c.com/index.php?post/2013/05/02/nearbyintf1 – Nicholas Wilson May 03 '13 at 19:09
  • See simple Java example, shuld be the same in C: http://stackoverflow.com/a/15790782/254109 – xmedeko Nov 05 '13 at 12:06

9 Answers9

47

Picture is worth a thousand words - try to draw equation f(k) :
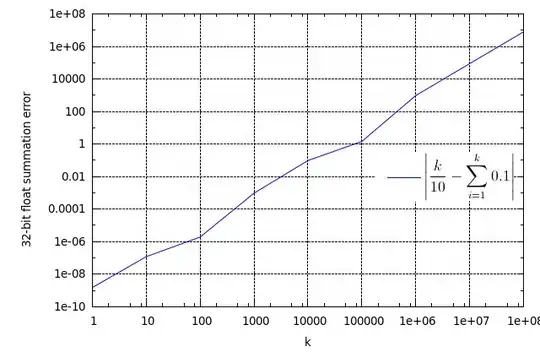
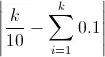enter image description here
and you will get such XY graph (X and Y are in logarithmic scale).
enter image description here
If computer could represent 32-bit floats without rounding error then for every k we should get zero. But instead error increases with bigger values of k because of floating point error accumulation.

hth!

Agnius Vasiliauskas
  • 10,935
  • 5
  • 50
  • 70
31
 for(double d = 0; d != 0.3; d += 0.1); // never terminates
Motti
  • 110,860
  • 49
  • 189
  • 262
13

Generally, floating point error refers to when a number that cannot be stored in the IEEE floating point representation.

Integers are stored with the right-most bit being 1, and each bit to the left being double that (2,4,8,...). It's easy to see that this can store any integer up to 2^n, where n is the number of bits.

The mantissa (decimal part) of a floating point number is stored in a similar way, but moving left to right, and each successive bit being half of the value of the previous one. (It's actually a little more complicated than this, but it will do for now).

Thus, numbers like 0.5 (1/2) are easy to store, but not every number <1 can be created by adding a fixed number of fractions of the form 1/2, 1/4, 1/8, ...

A really simple example is 0.1, or 1/10. This can be done with an infinite series (which I can't really be bothered working out), but whenever a computer stores 0.1, it's not exactly this number that is stored.

If you have access to a Unix machine, it's easy to see this:

Python 2.5.1 (r251:54863, Apr 15 2008, 22:57:26) 
[GCC 4.0.1 (Apple Inc. build 5465)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> 0.1
0.10000000000000001
>>>

You'll want to be really careful with equality tests with floats and doubles, in whatever language you are in.

(As for your example, 0.2 is another one of those pesky numbers that cannot be stored in IEEE binary, but as long as you are testing inequalities, rather than equalities, like p <= 0.2, then you'll be okay.)

Matthew Schinckel
  • 35,041
  • 6
  • 86
  • 121
9

Here's one that caught me :

 round(256.49999) == 256
roundf(256.49999) == 257

doubles and floats have different precision, so the first will be represented as 256.49999000000003, and the second one as 256.5, and will thus be rounded differently

Gabriel Ravier
  • 358
  • 1
  • 6
  • 17
Rory O'Bryan
  • 1,894
  • 14
  • 22
8

This is the simplest that comes to my mind, that should work with many languages is simply:

0.2 + 0.1

Here are some examples with the REPLs that come into my mind, but should return this result on any IEEE754-compliant language.

Python

>>> 0.2 + 0.1
0.30000000000000004

Kotlin

0.2 + 0.1
res0: kotlin.Double = 0.30000000000000004

Scala

scala> 0.2 + 0.1
val res0: Double = 0.30000000000000004

Java

jshell> 0.2 + 0.1
$1 ==> 0.30000000000000004

Ruby

irb(main):001:0> 0.2 + 0.1
=> 0.30000000000000004
Danilo Pianini
  • 966
  • 8
  • 19
7

A simple example in C that caught me a while back :

double d = 0;
sscanf("90.1000", "%lf", &d);
printf("%0.4f", d);

This prints 90.0999

This was in a function that converted angles in DMS to radians.

Why does it not work in the above case?

Nathan S.
  • 5,244
  • 3
  • 45
  • 55
SmacL
  • 22,555
  • 12
  • 95
  • 149
  • 3
    As an anonymous user pointed out, with `sscanf` the "f" conversion specifier requires a `float` argument, not a `double` (however, "f" means `double` to `printf` -- yes it's confusing). The "lf" modified conversion specifier should be used to make `sscanf` work with a `double`. – Dan Moulding Oct 07 '11 at 12:05
6

I like this one from a Python interpreter: 

Python 2.7.10 (default, Oct  6 2017, 22:29:07) 
[GCC 4.2.1 Compatible Apple LLVM 9.0.0 (clang-900.0.31)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> 0.1+0.2
0.30000000000000004
>>>
Samuel Li
  • 337
  • 5
  • 6
2

super simple (Python):

a = 10000000.1
b = 1/10
print(a - b == 10000000)
print ('a:{0:.20f}\nb:{1:.20f}'.format(a, b))

prints (depending on the platform) something like:

False                                                                                                                                 
a:10000000.09999999962747097015                                                                                                       
b:0.10000000000000000555
formiaczek
  • 385
  • 3
  • 7
  • 1
    What language is this? The question is tagged C++, where this code makes no sense at all (`1/10` is exactly representable in floating-point, it is `0.00000`) – Ben Voigt May 10 '21 at 21:25
0

I think Ruby has a good example in its documentation:

sum = 0
10_000.times do
  sum = sum + 0.0001
end
print sum #=> 0.9999999999999062
x-yuri
  • 16,722
  • 15
  • 114
  • 161