Fortran - Point in STL

Question

I am trying to fill a STL file with points in Fortran. I have written a basic code but it is not working.

My method has been to use a random number generator to generate a point. I then normalize this point to the dimensions of the STL bounding box.

I then throw out the "z" coordinate for the the first triangle in the STL. I check if the random point is with the max and min value of the "x" and "y" coordinate of the first triangle. If so I project the random point vertically onto the triangle plane and calculate the "z" value should it intersect with the plane. I then check if the z value of the random point is less than the value of the projected point (Ray casting). If yes I increase a counter, which is initially set to zero, by one.

I do this for every triangle in the STL. If the counter is even the random point is outside the volume, if it is odd the random point is inside the volume and the point is stored.

I then generate a new random point and start again. I have included the important code below. Apologies for the length (lots of comments and blank lines for readability).

! Set inital counter for validated points
k = 1

! Do for all randomly generated points
DO i=1,100000

  ! Create a random point with coordinates x, y and z.
  CALL RANDOM_NUMBER(rand)

  ! Normalise the random coordinates to the bounding box.
  rand(1:3) = (rand(1:3) * (cord(1:3) - cord(4:6))) + cord(4:6)

  ! Set the initial counter for the vertices
  j = 1

  ! Set the number of intersections with the random point and the triangle
  no_insect = 0 

  ! Do for all triangles in STL
  DO num = 1, notri

      ! Get the maximum "x" value for the current triangle
      maxtempx = MAXVAL(vertices(1,j:j+2))

      ! Get the minimum "x" value for the current triangle
      mintempx = MINVAL(vertices(1,j:j+2))

      ! If the random point is within the bounds continue
      IF (rand(1)>=mintempx .AND. rand(1)<=maxtempx) THEN

        ! Get the maximum "y" value for the current triangle
        maxtempy = MAXVAL(vertices(2,j:j+2))

        ! Get the minimum "y" value for the current triangle
        mintempy = MINVAL(vertices(2,j:j+2))    

        ! If the random point is within the bounds continue     
        IF (rand(2)>=mintempy .AND. rand(2)<=maxtempy) THEN

            ! Find the "z" value of the point as projected onto the triangle plane
            tempz = ((norm(1,num)*(rand(1)-vertices(1,j))) &
                +(norm(2,num)*(rand(2)-vertices(2,j))) &
                - (norm(3,num)*vertices(3,j))) / (-norm(3,num))

            ! If the "z" value of the randomly generated point goes vertically up
            ! through the projected point then increase the number of plane intersections
            ! by one. (Ray casting vertically up, could go down also).

            IF (rand(3)<= tempz) THEN
                no_insect = no_insect + 1   
            END IF  

        END IF
    END IF

    ! Go to the start of the next triangle
    j = j + 3
  END DO  

  ! If there is an odd number of triangle intersections not 
  ! including 0 intersections then store the point

  IF (MOD(no_insect,2)/=0 .AND. no_insect/=0) THEN
    point(k,1:3) = rand(1:3)
    WRITE(1,"(1X, 3(F10.8, 3X))") point(k,1), point(k,2), point(k,3)
    k = k + 1
  END IF

END DO 

My results have been complete rubbish (see images)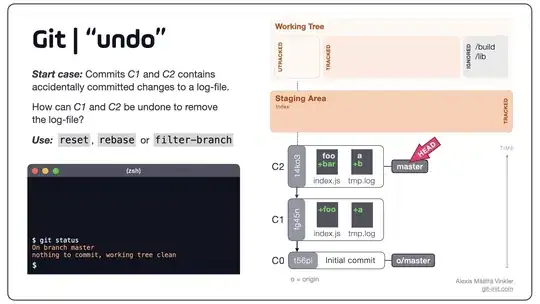 Image 1 - Test STL file (ship taken from here). Part of the program (code not shown) reads in binary STL files and stores the surface normals of each triangle and the vertices which make up this triangle. I then wrote the vertices to a text file and call GNUPLOT to connect the vertices of each triangle as show above. This plot is just a test to ensure that the STL files are being read and stored correctly. It does not use the surface normals. . Image 2 - This is a plot of the candidate points which were accepted as being inside the STL volume. (Stored in the final if loop shown in code above). These accepted points are then later written to a text file and plotted with GNUPLOT (NOT SHOWN). Had the algorithm worked this plot should be a point cloud of the triangulated mesh shown above. (It also plots the 8 bounding box coordinates to ensure that the random particles are generated in the correct range)

I appreciate that this does not take into account for points generated on vertices or rays which run parallel and intersect with edges. I just wanted to start with a rough code. Could you please advise if there is a problem with my methodology or code? Let me know if the question is too broad and I will delete it and try to be more specific.

Answer 1

I realized my code could be handy for others. I placed it at https://github.com/LadaF/Fortran---CGAL-polyhedra under the GNU GPL v3 license.

You can query, whether a point is inside a point or not. First, you read the file by cgal_polyhedron_read. You must store the type(c_ptr) :: ptree that is crated and use it in your next calls.

The function cgal_polyhedron_inside returns whether a point is inside a polyhedron, or not. It requires one reference point, which must be known to be outside.

When you are finished call cgal_polyhedron_finalize.

You must have the file as a purely tridiagonal manifold mesh in an OFF file. You can create it from the STL file using http://www.cs.princeton.edu/~min/meshconv/ .