long double
Wiki says: extended precision floating-point type. Actual properties unspecified. Unlike types float and double, it can be either 80-bit floating point format, the non-IEEE "double-double" or IEEE 754 quadruple-precision floating-point format if a higher precision format is provided, otherwise it is the same as double. See the article on long double for details.
- so it is hard to say what datatype you actually use (I prefer to use doubles)
constants
you are mixing integer and floating numbers together so the compiler has to decide what to use. Rewrite all floating numbers as 45 to 45.0 to be sure it is done correctly or a+i*h ... the i is int and h is double ...
integration
do not know the magnitude of the sum and range of your values but to improve floating precision you should avoid adding big and small values together because if the exponents are too different you loose too much of relevant mantissa bits.
So do the sum in two variables something like this (in C++):
double suml=0.0,sumh=0.0,summ=1000.0;
for (int i=0;i<n;i++)
{
suml+=...; // here goes the formula
if (fabs(suml)>summ) { sumh+=suml; suml=0; }
} sumh+=suml; suml=0;
// here the result is in sumh
summ is max magnitude of suml. It should be in relatively safe range in comparison to your sum iteration value for example 100-10000 times bigger then average value.
suml is the low magnitudes sum variable
sumh is the big magnitudes sum variable
if the range of your summed values is really big then you can add another if
if (fabs(value)>summ) sumh+=value; else suml+=value;
if it is even much bigger then you can sum into any count of variables in the same manner just divide the range of value to some meaning full ranges
formula
may be I am missing something but why are you mod-ing? As I see it you do not need the loop at all and also the ifs are obsolete so why to use a+i*h and not a+=h? it would improve performance and precision
something like this:
double sum,h;
h = (b-a)/double(n-1);
sum = 7.0*f(a); a+=h;
sum+=32.0*f(a); a+=h;
sum+=12.0*f(a); a+=h;
sum+=32.0*f(a); a+=h;
sum+= 7.0*f(a); a+=h;
return 2.0*h*sum/45.0;
// + the thing in the bullet 3 of coarse ...
// now I see you had an error in your constants !!!
[edit1] division implemented (not quadrupling)
//---------------------------------------------------------------------------
double f(double x)
{
// return x+0.2*x*x-0.001*x*x*x+2.0*cos(0.1*x)*tan(0.01*x*x)+25.0;
return x+0.2*x*x-0.001*x*x*x;
}
//---------------------------------------------------------------------------
double integrate_rect(double (*f)(double),double x0,double x1,int n)
{
int i;
double s=0.0,x=x0,dx=(x1-x0)/double(n-1);
for (i=0;i<n;i++,x+=dx) s+=f(x);
return s*dx;
}
//---------------------------------------------------------------------------
double integrate_Boole(double (*f)(double),double x0,double x1,int n)
{
n-=n%5; if (n<5) n=5;
int i;
double s=0.0,x=x0,dx=(x1-x0)/double(n-1);
for (i=0;i<n;i+=5)
{
s+= 7.0*f(x); x+=dx;
s+=32.0*f(x); x+=dx;
s+=12.0*f(x); x+=dx;
s+=32.0*f(x); x+=dx;
s+= 7.0*f(x); x+=dx;
}
s*=(2.0*dx)/(45.0);
return s*1.25; // this is the ratio to cover most cases
}
//---------------------------------------------------------------------------
void main()
{
int n=100000;
double x0=0.0,x1=+100.0,i0,i1;
i0=integrate_rect (f,x0,x1,n); cout << i0 << endl;
i1=integrate_Boole(f,x0,x1,n); cout << i1 << endl << i0/i1;
}
//---------------------------------------------------------------------------
I use mostly rectangular rule because on FPU is the quickest and most precise way. The more advanced approaches are better on paper but on computer the added overhead and rounding is usually slower/less precise then the same accuracy with rectangular rule
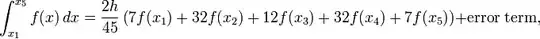
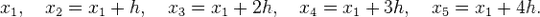
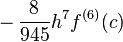 .
I fixed the problem with doubling the first term but I am not sure how to fix the possible doubling near the end of the loop. Also, the error is relatively large enough that I don't think that my only problem is the last four terms.
.
I fixed the problem with doubling the first term but I am not sure how to fix the possible doubling near the end of the loop. Also, the error is relatively large enough that I don't think that my only problem is the last four terms.