Methods of Integration for Discrete Data-points
The variable x is only continuous if you have a continuous functional form for it. If you have a
few discrete values (which it will be if you were to make a numpy array of discrete values), then
the array is no longer continuous as it can not resolve points in between two successive discrete
values of x.
So, assuming that you, in effect have an array of discrete data-points for both x and p, here
are my suggestions.
Get Acquainted With a Few Methods of Numerical Integration First
You can use any of the methods listed under "Methods for Integrating Functions given fixed samples".
INSIGHT What is important here is: in trapezoidal rule you
interpolate the space between the successive two points using a straight line. If you could
use a higher order polynomial (order ~ 2, 3, 4, etc.) then that could give you a better result for
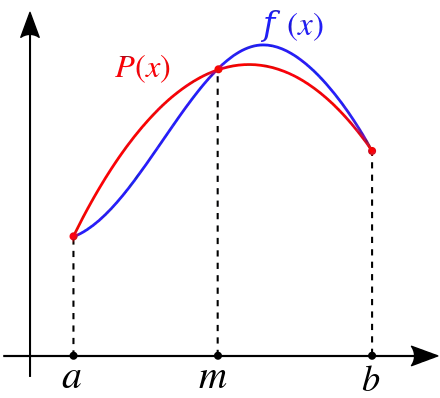
integration. Simpson's rule uses 2nd-order polynomial Simpson's Rule - Wolfram MathWorld.
 |
 |
| Simpson's Rule: Integrating area under a curve using quadratic polynomials |
An animation showing how Simpson's Rule is applied for integration |
Source: Wikipedia
Methods for Integrating Functions given fixed samples
trapezoid -- "Use trapezoidal rule to compute integral."
cumulative_trapezoid -- "Use trapezoidal rule to cumulatively compute integral."
simps -- "Use Simpson's rule to compute integral from samples."
romb -- "Use Romberg Integration to compute integral from
(2**k + 1) evenly-spaced samples."
Also see this for a quick example: Calculating the area under a curve given a set of coordinates, without knowing the function.
2. Area Under the Curve (AUC) using sklearn.metrics.auc
Integration is in essence the area under a curve (AUC). Scikit-learn library provides an easy
alternative to calculating AUC. In practice this also uses the trapezoidal rule and so, I do
not see any reason why this should be any/much different from what you already have
using numpy.trapz.
3. Consider using Other Methods
3.1. Romberg Integration
scipy.integrate.romb(y, dx=1.0, axis=- 1, show=False)
References

