9

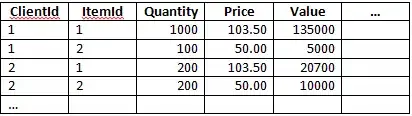
My data is:

>>> ts = pd.TimeSeries(data,indexconv)
>>> tsgroup = ts.resample('t',how='sum')
>>> tsgroup
2014-11-08 10:30:00    3
2014-11-08 10:31:00    4
2014-11-08 10:32:00    7
  [snip]
2014-11-08 10:54:00    5
2014-11-08 10:55:00    2
Freq: T, dtype: int64
>>> tsgroup.plot()
>>> plt.show()

indexconv are strings converted using datetime.strptime.

The plot is very edgy like this (these aren't my actual plots): enter image description here

How can I smooth it out like this: enter image description here

I know about scipy.interpolate mentioned in this article (which is where I got the images from), but how can I apply it for Pandas time series?

I found this great library called Vincent that deals with Pandas, but it doesn't support Python 2.6.

Alaa Ali
  • 896
  • 1
  • 12
  • 24

3 Answers3

11

Got it. With help from this question, here's what I did:

  1. Resample my tsgroup from minutes to seconds.

    \>>> tsres = tsgroup.resample('S')
\>>> tsres
2014-11-08 10:30:00     3
2014-11-08 10:30:01   NaN
2014-11-08 10:30:02   NaN
2014-11-08 10:30:03   NaN
...
2014-11-08 10:54:58   NaN
2014-11-08 10:54:59   NaN
2014-11-08 10:55:00     2
Freq: S, Length: 1501

  2. Interpolate the data using .interpolate(method='cubic'). This passes the data to scipy.interpolate.interp1d and uses the cubic kind, so you need to have scipy installed (pip install scipy) 1.

    \>>> tsint = tsres.interpolate(method='cubic')
\>>> tsint
2014-11-08 10:30:00    3.000000
2014-11-08 10:30:01    3.043445
2014-11-08 10:30:02    3.085850
2014-11-08 10:30:03    3.127220
...
2014-11-08 10:54:58    2.461532
2014-11-08 10:54:59    2.235186
2014-11-08 10:55:00    2.000000
Freq: S, Length: 1501

  3. Plot it using tsint.plot(). Here's a comparison between the original tsgroup and tsint:

1 If you're getting an error from .interpolate(method='cubic') telling you that Scipy isn't installed even if you do have it installed, open up /usr/lib64/python2.6/site-packages/scipy/interpolate/polyint.py or wherever your file might be and change the second line from from scipy import factorial to from scipy.misc import factorial.

Community
  • 1
  • 1
Alaa Ali
  • 896
  • 1
  • 12
  • 24
  • 3
    Depending on why you are doing this your solution may be highly problematic since it grossly misrepresents your actual data (e.g. at 10:40, 10:43). – tnknepp Nov 24 '14 at 18:49
  • Why do you say that? Aren't all the values from the actual data (which was aggregated by minute) stay the same, only values in the middle get interpolated to plot the graph. So all minute data is the same (`10:40` or `10:43`), but seconds (eg. `10:40:04`) get added to plot the graph. Both `tsgroup['2014-11-08 10:43:00']` and `tsint['2014-11-08 10:43:00']` return 3. NOTE: the y-axis in the subplots start from different points. – Alaa Ali Nov 24 '14 at 19:17
  • 1
    I do not understand what is going on under "interpolate's" hood, but just looking at the two plots you posted I get the impression that something is not right. From the blue plot I do not see any reason for the green plot to go above 5 around 10:40 (that being the key indicator in your plot), nor do I see any reason to suppose that you would have a dip between those the two points about 10:40. It just doesn't look right. I just see no reason to suggest that this interpolation is correct. – tnknepp Nov 24 '14 at 19:34
  • Yeah the dips are the values of the interpolated data. The values of the points 10:39, 10:40 and 10:41 in the original data **and** the interpolated data are 5, so the original data isn't changed, it's just that the humps around 10:40 are the values of the seconds in between the minutes that were calculated to make it look smoother. The interpolation is correct for the cubic method I used. If I were to use the linear method, there would be no humps and the interpolated plot would look exactly like the original, except it would be a "higher resolution". – Alaa Ali Nov 24 '14 at 19:55
  • 1
    Ok, so the humps are not real. What is the application for this? – tnknepp Nov 24 '14 at 20:25
  • Well the cubic function is probably mainly used for deriving data between points for "smoothness". It's a Spline function. Read more [here](http://en.wikipedia.org/wiki/Spline_(mathematics)) and [here](http://en.wikipedia.org/wiki/Spline_interpolation), and [this](http://docs.scipy.org/doc/scipy/reference/tutorial/interpolate.html) is the documentation from Scipy. – Alaa Ali Nov 24 '14 at 20:45
  • Sorry, I was wondering what type of data you are applying it to. – tnknepp Nov 24 '14 at 20:59
  • Oh, log analysis. I have data of a particular user activity that contains timestamps, so I'm aggregating the events in minute intervals and plotting over time. – Alaa Ali Nov 24 '14 at 21:13
  • 2
    My only comment would be that that's perfectly OK if the thing you want to do is make the data look more aesthetically pleasing to your own eye or those of others. On the other hand you wouldn't want to use that dip at 10:40 or the other one like it ~10:44 as being physically meaningful since it is merely an artifact of the spline fit. Spline fits will make any data look smooth but also can introduce artifacts as happened here. In my experience you can fine tune the spline fit parameters to make those kinds of things go away but you may be tuning them again on the next data set. – Charlie_M Jan 26 '16 at 22:33
4

You can smooth out your data with moving averages as well, effectively applying a low-pass filter to your data. Pandas supports this with the rolling() method.

Marcus
  • 41
  • 1
1

Check out scipy.interpolate.UnivariateSpline

tuomastik
  • 4,559
  • 5
  • 36
  • 48
mgcdanny
  • 1,082
  • 1
  • 13
  • 20