I will speak about your initial volcano-type-graph problem and not the made up one because they are totally different.
So I really thought this a lot and I believe I reached a solid conclusion. There are two options:
1. You know the equations of the lines, which would be really easy to work with.
2. You do not know the equation of the lines which means we need to work with an approximation.
Some geometry:
The function 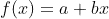 shows the equation of a line. For a given pair of coordinates (x, y), if y > the right hand side of the equation when you pass x in, then the point is above the line else below the line. The same concept stands if you have a curve (as in your case).
shows the equation of a line. For a given pair of coordinates (x, y), if y > the right hand side of the equation when you pass x in, then the point is above the line else below the line. The same concept stands if you have a curve (as in your case).
If you have the equations then it is easy to do the above in my code below and you are set. If not you need to make an approximation to the curve. To do that you will need the following code:
df=data.frame(x=seq(2,16,by=2),y=seq(2,16,by=2),lab=paste("label",seq(2,16,by=2),sep=''))
make_vector <- function(df) {
lab <- vector()
for (i in 1:nrow(df)) {
this_row <- df[i,] #this will contain the three elements per row
if ( (this_row[1] < max(line1x) & this_row[2] > max(line1y) & this_row[2] < a + b*this_row[1])
|
(this_row[1] > min(line2x) & this_row[2] > max(line2y) & this_row[2] > a + b*this_row[1]) ) {
lab[i] <- this_row[3]
} else {
lab[i] <- <NA>
}
}
return(lab)
}
#this_row[1] = your x
#this_row[2] = your y
#this_row[3] = your label
df$labels <- make_vector(df)
plot(df[,1],df[,2])
# adding lines
lines(seq(1,15),seq(15,1),lwd=1, lty=2)
# adding labels
text(df[,1],df[,2],labels=df[,4],pos=3,col="red",cex=0.75)
The important bit is the function. Imagine that you have df as you created it with x,y and labs. You also will have a vector with the x,y coordinates for line1 and x,y coordinates for line2.
Let's see the condition of line1 only (the same exists for line 2 which is implemented on the code above):
this_row[1] < max(line1x) & this_row[2] > max(line1y) & this_row[2] < a + b*this_row[1]
#translates to:
#this_row[1] < max(line1x) = your x needs to be less than the max x (vertical line in graph below
#this_row[2] > max(line1y) = your y needs to be greater than the max y (horizontal line in graph below
#this_row[2] < a + b*this_row[1] = your y needs to be less than the right hand side of the equation (to have a point above i.e. left of the line)
#check below what the line is
This will make something like the below graph (this is a bit horrible and also magnified but it is just a reference. Visualize it approximating your lines):

The above code would pick all the points in the area above the triangle and within the y=1 and x=1 lines.
Finally the equation:
Having 2 points' coordinates you can figure out a line's equation solving a system of two equations and 2 parameters a and b. (y = a +bx by replacing y,x for each point)
The 2 points to pick are the two points closest to the tangent of the first line (line1). Chose those arbitrarily according to your data. The closest to the tangent the better. Just plot the spots and eyeball.
Having done all the above you have your points with your labels (approximately at least).
And that is the only thing you can do!
Long talk but hope it helps.
P.S. I haven't tested the code because I have no data.
 Thanks
Thanks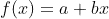 shows the equation of a line. For a given pair of coordinates (x, y), if y > the right hand side of the equation when you pass x in, then the point is above the line else below the line. The same concept stands if you have a curve (as in your case).
shows the equation of a line. For a given pair of coordinates (x, y), if y > the right hand side of the equation when you pass x in, then the point is above the line else below the line. The same concept stands if you have a curve (as in your case).