I want to improve a collision system.
Right now I detect if 2 irregular objects collide if their bounding rectangles collide.
I want to obtain the for rectangle the corresponding ellipse while for the other one to use a circle. I found a method to obtain the ellipse coordinates but I have a problem when I try to detect if it intersects the circle.
Do you know a algorithm to test if a circle intersects an ellipse?
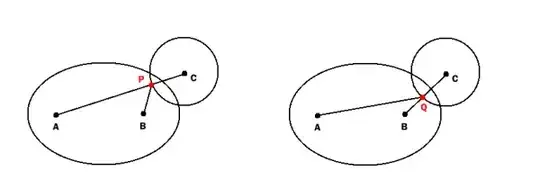
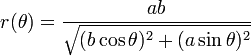Short answer: Solving exactly for whether the two objects intersect is complicated enough to be infeasible for the purpose of collision detection. Discretize your ellipse as an n-sided polygon for some n (depending on how accurate you need to be) and do collision detection with that polygon.
Long answer: If you insist on determining if the smooth ellipse and circle intersect, there are two main approaches. Both involve solving first for the closest point to the circle's center on the ellipse, and then comparing that distance to the circle's radius.
Approach 1: Use a parametrization of the ellipse. Transform your coordinates so that the ellipse is at the origin, with its axes aligned to the x-y axes. That is:
The equation of the ellipse is then given by a cos(t), b sin(t). To find the closest point, we want to minimize the square distance
|| (a cos t, b sin t) - c ||^2. As Jean points out, this is "just calculus": take a derivative, and set it equal to 0. Unless I'm missing something, though, solving the resulting (quite nasty) equation for t is not possible analytically, and must be approximated using e.g. Newton's Method.
Plug in the t you find into the parametric equation to get the closest point.
t.Approach 2: Use multidimensional calculus. No change of coordinates is necessary.
Finding the point on the ellipse closest to the center of the circle can then be phrased as a constrained minimization problem:
Minimize ||(x,y) - c||^2 subject to g(x,y) = 0
(Minimizing the square distance is equivalent to minimizing the distance, and much more pleasant to deal with since it's a quadratic polynomial in x,y.)
To solve the constrained minimization problem, we introduce Lagrange multiplier lambda, and solve the system of equations
2 * [ (x,y) -c ] + lambda * Jg(x,y) = 0
g(x,y) = 0
Here Jg is the gradient of g. This is a system of three (nonlinear) equations in three unknowns: x, y, and lambda. We can solve this system using Newton's Method, and the (x,y) we get is the closest point to the circle's center.
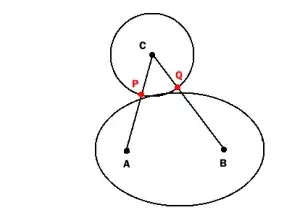
Caveat: both of these approaches technically solve for the point which extremizes the distance to the circle's center. Thus the point found might be the furthest point from the circle, and not the closest. For both methods, seeding your solve with a good initial guess (the center of the circle works well for Method 2; you're on your own for Method 1) will reduce this danger.
Potential Third Approach?: It may be possible to directly solve for the roots of the system of two quadratic equations in two variables representing the circle and ellipse. If a real root exists, the objects intersect. The most direct way of solving this system, again using a numerical algorithm like Newton's Method, won't help because lack of convergence does not necessary imply nonexistence of a real root. For two quadratic equations in two variables, however, there may exist a specialized method that's guaranteed to find real roots, if they exist. I myself can't think of a way of doing this, but you may want to research it yourself (or see if someone on stackoverflow can elaborate.)
An ellipse is defined a the set of points whose sum of the distance to point A and the distance to point B is constant e. (A and B are called the foci of the ellipse).
All Points P, whose sum AP + BP is less than e, lie within the ellipse.
A circle is defined as the set of points whose distance to point C is r.
A simple test for intersection of circle and ellipse is following:
Find
P as the intersection of the circle and the line AC and
Q as the intersection of the circle and the line BC.
Circle and ellipse intersect (or the circle lies completely within the ellipse) if
AP + BP <= e or AQ + BQ <= e
EDIT:
After the comment of Martin DeMello and adapting my answer accordingly I thought more about the problem and found that the answer (with the 2nd check) still doesn't detect all intersections:
If circle and ellipse are intersecting only very scarcely (just a little more than being tangent) P and Q will not lie within the ellipse:
So the test described above detects collision only if the overlap is "big enough". Maybe it is good enough for your practical purposes, although mathematically it is not perfect.
I know that it's too late but I hope it would help somebody. My approach to solve this problem was to interpolate the ellipse into an n-dimensions polygon, then to construct a line between every 2 points and find whether the circle intersects with any of the lines or not. This doesn't provide the best performance, but it is handy and easy to implement.
To interpolate the ellipse to an n-dimensions polygon, you can use:
float delta = (2 * PI) / n;
std::vector<Point*> interpolation;
for(float t = 0; t < (2 * PI); t += delta) {
float x = rx * cos(t) + c->get_x();
float y = ry * sin(t) + c->get_y();
interpolation.push_back(new Point(x, y));
}
c: The center of the ellipse. rx: The radius of x-aligned axis of the ellipse. ry: The radius of y-aligned axis of the ellipse.
Now we have the interpolation points, we can find the intersection between the circle and the lines between every 2 points. One way to find the line-cricle intersection is described here, an intersection occurs if an intersection occurred between any of the lines and the circle.
Hope this helps anybody.
Enlarge the ellipse's major and minor radii by the radius of the circle. Then test if the center of the given circle is within this new larger ellipse by summing the distances to the foci of the enlarged ellipse.
This algorithm is quite efficient. You can early-out if the given circle doesn't intersect a circle which circumscribes the ellipse. This is slower than a bounding box test, but finding the bounding box of a non-axis-aligned ellipse is tricky.
find the point on the ellipse closest to the center of the circle
and then check if the distance from this point is smaller than the radius of the circle
if you need help doing this just comment, but it's simply calculus
edit: here's a ways towards the solution, since there is something wrong with curds
given center α β on the ellipse
and (for lack of remembering the term) x radius a, y radius b
the parametrization is
r(Θ) = (ab)/( ( (BcosΘ)^2 + (asinΘ)^2 )^.5)
x(Θ) = α + sin(Θ)r(Θ)
y(Θ) = β + cos(Θ)r(Θ)
and then just take the circle with center at (φ, ψ) and radius r then the distance d(Θ) = ( (φ - x(Θ))^2 + (ψ - y(Θ) )^2)^.5
the minimum of this distance is when d'(Θ) = 0 (' for the derivative)
d'(Θ) = 1/d(Θ) * (-φx'(Θ) + x(Θ)x'(Θ) - ψy'(Θ) + y(Θ)y'(Θ) )
==>
x'(Θ) * (-φ + x(Θ)) = y'(Θ) * (ψ - y(Θ))
and keep going and going and hopefully you can solve for Θ
The framework you're working in might have things to help you solve this, and you could always take the easy way out and approximate roots via Newton's Method
if a circle and an ellipse collide, then either their boundaries intersect 1, 2, 3, or 4 times(or infinitely many in the case of a circular ellipse that coincides with the circle), or the circle is within the ellipse or vice versa.
I'm assuming the circle has an equation of (x - a)^2 + (y - b)^2 <= r^2 (1) and the ellipse has an equation of [(x - c)^2]/[d^2] + [(y - e)^2]/[f^2] <= 1 (2)
To check whether one of them is inside the other, you can evaluate the equation of the circle at the coordinates of the center of the ellipse(x=c, y=e), or vice versa, and see if the inequality holds.
to check the other cases in which their boundaries intersect, you have to check whether the system of equations described by (1) and (2) has any solutions.
you can do this by adding (1) and (2), giving you
(x - a)^2 + (y - b)^2 + [(x - c)^2]/[d^2] + [(y - e)^2]/[f^2] = r^2 + 1
next you multiply out the terms, giving
x^2 - 2ax + a^2 + y^2 - 2by + b^2 + x^2/d^2 - 2cx/d^2 + c^2/d^2 + y^2/f^2 - 2ey/f^2 + e^2/f^2 = r^2 + 1
collecting like terms, we get
(1 + 1/d^2)x^2 - (2a + 2c/d^2)x + (1 + 1/f^2)y^2 - (2b + 2e/f^2)y = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2
now let m = (1 + 1/d^2), n = -(2a + 2c/d^2), o = (1 + 1/f^2), and p = -(2b + 2e/f^2)
the equation is now mx^2 + nx + oy^2 + py = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2
now we need to complete the squares on the left hand side
m[x^2 + (n/m)x] + o[y^2 + (p/o)y] = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2
m[x^2 + (n/m)x + (n/2m)^2 - (n/2m)^2] + o[y^2 + (p/o)y + (p/2o)^2 - (p/2o)^2] = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2
m[(x + n/2m)^2 - (n/2m)^2] + o[(y + p/2o)^2 - (p/2o)^2] = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2
m(x + n/2m)^2 - m(n/2m)^2 + o(y + p/2o)^2 - o(p/2o)^2 = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2
m(x + n/2m)^2 + o(y + p/2o)^2 = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2 + m(n/2m)^2 + o(p/2o)^2
this system has a solution iff 11 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2 + m(n/2m)^2 + o(p/2o)^2 >= 0
There you have it, if I didn't make any algebraic mistakes. I don't know how much you can simplify the resulting expression, so this solution might be quite computationally expensive if you're going to check for many circles/ellipses
Forget about a mathematical solution. As you can easily see by drawing, you can have up to four solutions, and thus likely a fourth grade polynomial.
Instead just do a binary search along the edge of one of the figures. It is easy to determine if a point lies within an ellipse and even more so in a circle (just see if distance is shorter than radius).
If you really want to go for the maths, Wolfram MathWorld has a nice article here: http://mathworld.wolfram.com/Circle-EllipseIntersection.html but be warned, you'll still have to write a polynomial equation solver, probably using something like binary search.
Supposing: the ellipse is centred at the origin and with the semi-major axis (of length a) oriented along the x axis, and with a semi-minor axis of length b; E2 is the eccentricity squared, ie (aa-bb)/(a*a); the circle is centred at X,Y and of radius r.
The easy cases are: the circle centre is inside the ellipse (ie hypot(X/a, Y/b) <= 1) so there is an intersection; the circle centre is outside a circle centred at 0 of radius a+r (ie hypot(X,Y) > a+r) so there isn't an intersection.
One approach for the other cases is to compute the geodetic coordinates (latitude, height) of the circle centre. The circle intersects the ellipse if and only if the height is less than the radius.
The geodetic latitude of a point on an ellipse is the angle the normal to the ellipse at the point makes with the x axis, and the height of a point outside the ellipse is the distance of the point from the point on the ellipse closest to it. Note the geodetic latitude is not same as the polar angle from the ellipse centre to the point unless the ellipse is in fact circular.
In formulae the conversion from geodetic coordinates lat,ht to cartesian coordinates X,Y is X = (nu+ht)*cos(lat), Y = (nu * (1-E2) + ht)*sin(lat) where nu = a/sqrt( 1 - E2*sin(lat)sin(lat)). The point on the ellipse closest to X,Y is the point with the same latitude, but zero height, ie x = nucos(lat), y = nu * (1-E2) * sin(lat). Note that nu is a function of latitude.
Unfortunately the process of finding lat,ht from X,Y is an iterative one. One approach is to first find the latitude, and then the height.
A little algebra shows that the latitude satisfies lat = atan2( Y+ E2*nusin(lat), X) which can be used to compute successive approximations to the latitude, starting at lat = atan2( Y, X(1.0-E2)), or (more efficiently) can be solved using newton's method.
The larger E2 is, ie the flatter the ellipse is, the more iterations will be required. For example if the ellipse is nearly circular (say E2<0.1) then five iterations will get x,y below to within a*1e-12, but if the ellipse is very flat, e.g. E2=0.999 you'll need around 300 iterations to get the same accuracy!
Finally, given the latitude, the height can be computed by computing (x,y): x = nucos(lat), y = nu(1-E2)*sin(lat) and then h is the distance from x,y to the circle centre, h = hypot( X-x, Y-y)
I wanted to provide some input into the more general problem involving contact between two ellipses. Calculating the distance of closest approach of two ellipses was a long standing problem and was only solved analytically within the last ten years-it is by no means simple. The solution to the problem may be found here http://www.e-lc.org/docs/2007_01_17_00_46_52/.
The general method to determine if there is contact between two ellipses is to first calculate the distance of closest approach of the ellipses in their current configuration and then subtract this from their current magnitude of separation. If this result is less than or equal to 0, then they are in contact.
If anyone is interested I can post code that calculates the distance of closest approach--it's in C++. The code is for the general case of two arbitrary ellipses, but you can obviously do it for a circle and ellipse, since a circle is an ellipse with equal minor and major axes.
This isn't that hard. user168715's answer is generally right, but doing calculus isn't necessary. Just trigonometry.
Find the angle between the center of the two objects. Using this you can find the closest point to the circle's center on the ellipse using the polar-form:
(Taken from Wikipedia article on Ellipses)
Now compare the distance between the two object centers, subtracting the ellipse radius and circle radius.
Maybe I'm missing something; maybe ArcTan/Cos/Sin are slow -- but I don't think so, and there should be fast-approximations if needed.
