How to apply piecewise linear fit for a line with both positive and negative slopes in Python?

Question

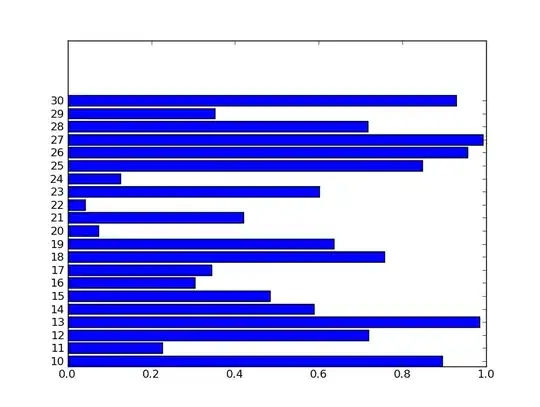
I have data provided in the code which have negative and positive slopes as shown in figure:

Using the code applied in this post Fit a curve for data made up of two distinct regimes, I created this code. It works for same slopes either both positive or both negative, but when one is positive and other negative, it is not able to fit the lines properly.

from scipy import optimize
from scipy import optimize, interpolate
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
import numpy as np


x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20])
y = np.array([4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 22, 20, 18, 16, 14, 12, 10, 8, 6, 4])


def two_lines(x, a, b, c, d):
    one = a*x + b
    two = c*x + d
    return np.maximum(one, two)


'''Compute approximate slope and intercept of the two lines'''
poly_low = np.polyfit(x[0:int(0.5*(len(x) + 1))], y[0:int(0.5*(len(x) + 1))], deg=1)
poly_high = np.polyfit(x[int(0.5*(len(x) + 1)):len(x)], y[int(0.5*(len(x) + 1)):len(x)], deg=1)

# This part of the code credit goes to askewchan
pw0 = (poly_low[0], poly_low[1], poly_high[0], poly_high[1]) # a guess for slope, intercept, slope, intercept
pw, cov = curve_fit(two_lines, x, y, pw0)
crossover = (pw[3] - pw[1]) / (pw[0] - pw[2])


figure = plt.figure(figsize=(5.15, 5.15))
figure.clf()
plot = plt.subplot(111)
plt.plot(x, y, 'o', x, two_lines(x, *pw), '-')
plot.set_ylabel('Y', labelpad = 6)
plot.set_xlabel('X', labelpad = 6)
plt.show()

Output

For different slopes:

For same slope both negative (works fine for positive slopes also):

I have two questions:

1. How to apply piecewise linear fits for such cases in Python?
2. How to extend it to three or more regimes?

Answer 1

You could use masked regions for piece-wise functions:

def two_lines(x, a, b, c, d):
    out = np.empty_like(x)
    mask = x < 10
    out[mask] = a*x[mask] + b
    out[~mask] = c*x[~mask] + d
    return out

First test with two different positive slopes:

x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
              17, 18, 19, 20])
y = np.array([4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 25, 26, 27, 28, 29,
    30, 31, 32, 33, 34])

Second test with a positive and a negative slope (data from your example):

Answer 2

What you have basically works for the specific problem and data that you're presenting, but it is the wrong way to solve this problem more generally. It can not be easily expanded to wider range of circumstances, for example, multiple segments, data with more complicated transitions between the linear segments, situations where you need to tune specific aspects of the fit, etc. The primary reason is that your treating an easy specific and highly constrained problem (fitting multiple, non-overlapping line segments) in the most general and difficult way (a high-dimensional, multiparameter fit). Amongst other problems, this generalization will make it harder for the fit to land in the correct region of the parameter space. This is a problem about easy localized fits that you're trying to solve with a difficult generalized global solution. I see the appeal, but it's unlikely to work for anything but toy examples.

That said, what you have will work for toy example as long as one starts with the correct sign for the slopes. At least it works starting from (1,1,-1,1) and (10,10,-10,10), but you also need to know these given your definition of two_lines, so I'm not really assuming anything you didn't. Also, you need to define two_lines so it can match (your original had the downward triangle rather than upward, which is also probably why it worked for the two "negative sloped" lines -- not because they are negatively sloped but because they can be matched by your original definition).

from scipy import optimize
from scipy import optimize, interpolate
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
import numpy as np

x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20])
y = np.array([4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 22, 20, 18, 16, 14, 12, 10, 8, 6, 4])

def two_lines(x, a, b, c, d):
    one = a*x + b
    two = c*x + d
    return np.minimum(one, two)

pw, cov = curve_fit(two_lines, x, y, (10, 10, -10, 10))

figure = plt.figure(figsize=(5.15, 5.15))
figure.clf()
plot = plt.subplot(111)
plt.plot(x, y, 'o')
plt.plot(x, two_lines(x, *pw), '-')
plot.set_ylabel('Y', labelpad = 6)
plot.set_xlabel('X', labelpad = 6)
plt.show()

The obvious alternative is to just move along your curve with independent piecewise linear fits. This approach is easy, fast, flexible, and probably matches your intuition better. This approach is also easily expanded to an infinite number of segments (whereas your global solution probably maxes out at two), and also allows the fits to linear section to not be messed up by sections of the curve which are not perfectly linear (for example, rounded transitions).