If I have an image, in which there is a page of text shot on a uniform background, how can I auto detect the boundaries between the paper and the background?
An example of the image I want to detect is shown below. The images that I will be dealing with consist of a single page on a uniform background and they can be rotated at any angle.
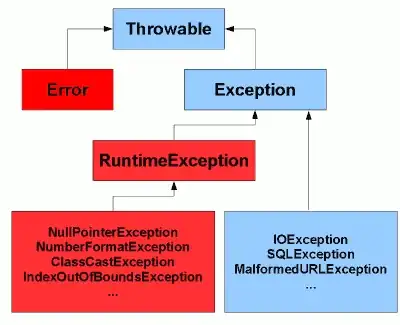
One simple method would be to threshold the image by some known value once you convert the image to grayscale. The problem with that approach is that we are applying a global threshold and so some of the paper at the bottom of the image will be lost if you make the threshold too high. If you make the threshold too low, then you'll certainly get the paper, but you'll include a lot of the background pixels too and it will probably be difficult to remove those pixels with post-processing.
One thing I can suggest is to use an adaptive threshold algorithm. An algorithm that has worked for me in the past is the Bradley-Roth adaptive thresholding algorithm. You can read up about it here on a post I commented on a while back:
Bradley Adaptive Thresholding -- Confused (questions)
However, if you want the gist of it, an integral image of the grayscale version of the image is taken first. The integral image is important because it allows you to calculate the sum of pixels within a window in O(1) complexity. However, the calculation of the integral image is usually O(n^2), but you only have to do that once. With the integral image, you scan neighbourhoods of pixels of size s x s and you check to see if the average intensity is less than t% of the actual average within this s x s window then this is pixel classified as the background. If it's larger, then it's classified as being part of the foreground. This is adaptive because the thresholding is done using local pixel neighbourhoods rather than using a global threshold.
I've coded an implementation of the Bradley-Roth algorithm here for you. The default parameters for the algorithm are s being 1/8th of the width of the image and t being 15%. Therefore, you can just call it this way to invoke the default parameters:
out = adaptiveThreshold(im);
im is the input image and out is a binary image that denotes what belongs to foreground (logical true) or background (logical false). You can play around with the second and third input parameters: s being the size of the thresholding window and t the percentage we talked about above and can call the function like so:
out = adaptiveThreshold(im, s, t);
Therefore, the code for the algorithm looks like this:
function [out] = adaptiveThreshold(im, s, t)
%// Error checking of the input
%// Default value for s is 1/8th the width of the image
%// Must make sure that this is a whole number
if nargin <= 1, s = round(size(im,2) / 8); end
%// Default value for t is 15
%// t is used to determine whether the current pixel is t% lower than the
%// average in the particular neighbourhood
if nargin <= 2, t = 15; end
%// Too few or too many arguments?
if nargin == 0, error('Too few arguments'); end
if nargin >= 4, error('Too many arguments'); end
%// Convert to grayscale if necessary then cast to double to ensure no
%// saturation
if size(im, 3) == 3
im = double(rgb2gray(im));
elseif size(im, 3) == 1
im = double(im);
else
error('Incompatible image: Must be a colour or grayscale image');
end
%// Compute integral image
intImage = cumsum(cumsum(im, 2), 1);
%// Define grid of points
[rows, cols] = size(im);
[X,Y] = meshgrid(1:cols, 1:rows);
%// Ensure s is even so that we are able to index the image properly
s = s + mod(s,2);
%// Access the four corners of each neighbourhood
x1 = X - s/2; x2 = X + s/2;
y1 = Y - s/2; y2 = Y + s/2;
%// Ensure no co-ordinates are out of bounds
x1(x1 < 1) = 1;
x2(x2 > cols) = cols;
y1(y1 < 1) = 1;
y2(y2 > rows) = rows;
%// Count how many pixels there are in each neighbourhood
count = (x2 - x1) .* (y2 - y1);
%// Compute row and column co-ordinates to access each corner of the
%// neighbourhood for the integral image
f1_x = x2; f1_y = y2;
f2_x = x2; f2_y = y1 - 1; f2_y(f2_y < 1) = 1;
f3_x = x1 - 1; f3_x(f3_x < 1) = 1; f3_y = y2;
f4_x = f3_x; f4_y = f2_y;
%// Compute 1D linear indices for each of the corners
ind_f1 = sub2ind([rows cols], f1_y, f1_x);
ind_f2 = sub2ind([rows cols], f2_y, f2_x);
ind_f3 = sub2ind([rows cols], f3_y, f3_x);
ind_f4 = sub2ind([rows cols], f4_y, f4_x);
%// Calculate the areas for each of the neighbourhoods
sums = intImage(ind_f1) - intImage(ind_f2) - intImage(ind_f3) + ...
intImage(ind_f4);
%// Determine whether the summed area surpasses a threshold
%// Set this output to 0 if it doesn't
locs = (im .* count) <= (sums * (100 - t) / 100);
out = true(size(im));
out(locs) = false;
end
When I use your image and I set s = 500 and t = 5, here's the code and this is the image I get:
im = imread('https://i.stack.imgur.com/MEcaz.jpg');
out = adaptiveThreshold(im, 500, 5);
imshow(out);
You can see that there are some spurious white pixels at the bottom white of the image, and there are some holes we need to fill in inside the paper. As such, let's use some morphology and declare a structuring element that's a 15 x 15 square, perform an opening to remove the noisy pixels, then fill in the holes when we're done:
se = strel('square', 15);
out = imopen(out, se);
out = imfill(out, 'holes');
imshow(out);
This is what I get after all of that:
Not bad eh? Now if you really want to see what the image looks like with the paper segmented, we can use this mask and multiply it with the original image. This way, any pixels that belong to the paper are kept while those that belong to the background go away:
out_colour = bsxfun(@times, im, uint8(out));
imshow(out_colour);
We get this:
You'll have to play around with the parameters until it works for you, but the above parameters were the ones I used to get it working for the particular page you showed us. Image processing is all about trial and error, and putting processing steps in the right sequence until you get something good enough for your purposes.
Happy image filtering!
