I finally came up with the correct solution, thanks to @Amy Teegarden for getting me going in the right direction. I thought I would share the final solution here for others to reference! Here is the final result:
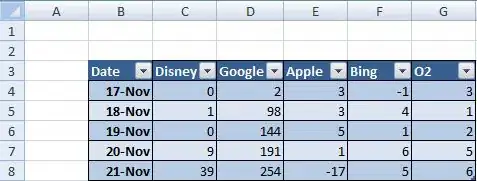
Following is a true probability axis scale, using the normal CDF and its inverse, PPF, functions paramterized by mu and sigma.
import numpy as np
from matplotlib import scale as mscale
from matplotlib import transforms as mtransforms
from matplotlib.ticker import FormatStrFormatter, FixedLocator
from scipy.stats import norm
class ProbScale(mscale.ScaleBase):
"""
Scales data in range 0 to 100 using a non-standard log transform
This scale attempts to replicate "probability paper" scaling
The scale function:
A piecewise combination of exponential, linear, and logarithmic scales
The inverse scale function:
piecewise combination of exponential, linear, and logarithmic scales
Since probabilities at 0 and 100 are not represented,
there is user-defined upper and lower limit, above and below which nothing
will be plotted. This defaults to .1 and 99 for lower and upper, respectively.
"""
# The scale class must have a member ``name`` that defines the
# string used to select the scale. For example,
# ``gca().set_yscale("mercator")`` would be used to select this
# scale.
name = 'prob_scale'
def __init__(self, axis, **kwargs):
"""
Any keyword arguments passed to ``set_xscale`` and
``set_yscale`` will be passed along to the scale's
constructor.
upper: The probability above which to crop the data.
lower: The probability below which to crop the data.
"""
mscale.ScaleBase.__init__(self)
upper = kwargs.pop("upper", 98) #Default to an upper bound of 98%
if upper <= 0 or upper >= 100:
raise ValueError("upper must be between 0 and 100.")
lower = kwargs.pop("lower", 0.2) #Default to a lower bound of .2%
if lower <= 0 or lower >= 100:
raise ValueError("lower must be between 0 and 100.")
if lower >= upper:
raise ValueError("lower must be strictly less than upper!.")
self.lower = lower
self.upper = upper
#This scale is best described by the CDF of the normal distribution
#This distribution is paramaterized by mu and sigma, these default vaules
#are provided to work generally well, but can be adjusted by the user if desired
mu = kwargs.pop("mu", 15)
sigma = kwargs.pop("sigma", 40)
self.mu = mu
self.sigma = sigma
#Need to enfore the upper and lower limits on the axes initially
axis.axes.set_xlim(lower,upper)
def get_transform(self):
"""
Override this method to return a new instance that does the
actual transformation of the data.
The ProbTransform class is defined below as a
nested class of this one.
"""
return self.ProbTransform(self.lower, self.upper, self.mu, self.sigma)
def set_default_locators_and_formatters(self, axis):
"""
Override to set up the locators and formatters to use with the
scale. This is only required if the scale requires custom
locators and formatters. Writing custom locators and
formatters: many helpful examples in ``ticker.py``.
In this case, the prob_scale uses a fixed locator from
0.1 to 99 % and a custom no formatter class
This builds both the major and minor locators, and cuts off any values
above or below the user defined thresholds: upper, lower
"""
#major_ticks = np.asarray([.2,.5,1,2,5,10,20,30,40,50,60,70,80,90,95,98])
major_ticks = np.asarray([.2,1,2,5,10,20,30,40,50,60,70,80,90,98]) #removed a couple ticks to make it look nicer
major_ticks = major_ticks[np.where( (major_ticks >= self.lower) & (major_ticks <= self.upper) )]
minor_ticks = np.concatenate( [np.arange(.2, 1, .1), np.arange(1, 2, .2), np.arange(2,20,1), np.arange(20, 80, 2), np.arange(80, 98, 1)] )
minor_ticks = minor_ticks[np.where( (minor_ticks >= self.lower) & (minor_ticks <= self.upper) )]
axis.set_major_locator(FixedLocator(major_ticks))
axis.set_minor_locator(FixedLocator(minor_ticks))
def limit_range_for_scale(self, vmin, vmax, minpos):
"""
Override to limit the bounds of the axis to the domain of the
transform. In the case of Probability, the bounds should be
limited to the user bounds that were passed in. Unlike the
autoscaling provided by the tick locators, this range limiting
will always be adhered to, whether the axis range is set
manually, determined automatically or changed through panning
and zooming.
"""
return max(self.lower, vmin), min(self.upper, vmax)
class ProbTransform(mtransforms.Transform):
# There are two value members that must be defined.
# ``input_dims`` and ``output_dims`` specify number of input
# dimensions and output dimensions to the transformation.
# These are used by the transformation framework to do some
# error checking and prevent incompatible transformations from
# being connected together. When defining transforms for a
# scale, which are, by definition, separable and have only one
# dimension, these members should always be set to 1.
input_dims = 1
output_dims = 1
is_separable = True
def __init__(self, upper, lower, mu, sigma):
mtransforms.Transform.__init__(self)
self.upper = upper
self.lower = lower
self.mu = mu
self.sigma = sigma
def transform_non_affine(self, a):
"""
This transform takes an Nx1 ``numpy`` array and returns a
transformed copy. Since the range of the Probability scale
is limited by the user-specified threshold, the input
array must be masked to contain only valid values.
``matplotlib`` will handle masked arrays and remove the
out-of-range data from the plot. Importantly, the
``transform`` method *must* return an array that is the
same shape as the input array, since these values need to
remain synchronized with values in the other dimension.
"""
masked = np.ma.masked_where( (a < self.upper) & (a > self.lower) , a)
#Get the CDF of the normal distribution located at mu and scaled by sigma
#Multiply these by 100 to put it into a percent scale
cdf = norm.cdf(masked, self.mu, self.sigma)*100
return cdf
def inverted(self):
"""
Override this method so matplotlib knows how to get the
inverse transform for this transform.
"""
return ProbScale.InvertedProbTransform(self.lower, self.upper, self.mu, self.sigma)
class InvertedProbTransform(mtransforms.Transform):
input_dims = 1
output_dims = 1
is_separable = True
def __init__(self, lower, upper, mu, sigma):
mtransforms.Transform.__init__(self)
self.lower = lower
self.upper = upper
self.mu = mu
self.sigma = sigma
def transform_non_affine(self, a):
#Need to get the PPF value for a, which is in a percent scale [0,100], so move back to probability range [0,1]
inverse = norm.ppf(a/100, self.mu, self.sigma)
return inverse
def inverted(self):
return ProbScale.ProbTransform(self.lower, self.upper)
# Now that the Scale class has been defined, it must be registered so
# that ``matplotlib`` can find it.
mscale.register_scale(ProbScale)
Also, to get the desired y-axis results, I discovered that the log-scale could indeed be used with a few extra tweaks to get a reasonable graph. This is the code used to force the log scale to have appropriate minor ticks:
axes.set_yscale('log', basey=10, subsy=[2,3,4,5,6,7,8,9])
Then you can modify the labeling with the locator and formatter:
#Adjust the yaxis labels and format
axes.yaxis.set_minor_locator(FixedLocator([200, 500, 1500, 2500, 3500, 4500, 5000, 6000, 7000, 8000, 9000, 15000, 20000, 25000, 30000, 35000, 40000, 45000, 50000]))
axes.yaxis.set_minor_formatter(FormatStrFormatter('%d'))
axes.yaxis.set_major_formatter(FormatStrFormatter('%d'))
So the complete axes maninputlation looks like this:
axes.set_ylabel('Discharge in CFS')
axes.set_xlabel('Exceedance Probability')
plt.setp(plt.xticks()[1], rotation=45)
#Adjust the scales of the x and y axis
axes.set_yscale('log', basey=10, subsy=[2,3,4,5,6,7,8,9])
axes.set_xscale('prob_scale', upper=98, lower=.2)
#Adjust the yaxis labels and format
axes.yaxis.set_minor_locator(FixedLocator([200, 500, 1500, 2500, 3500, 4500, 5000, 6000, 7000, 8000, 9000, 15000, 20000, 25000, 30000, 35000, 40000, 45000, 50000]))
axes.yaxis.set_minor_formatter(FormatStrFormatter('%d'))
axes.yaxis.set_major_formatter(FormatStrFormatter('%d'))
#Finally set the y-limit of the plot to be reasonable
axes.set_ylim((0, 2*pp['Q'].max()))
#Invert the x-axis
axes.invert_xaxis()
#Turn on major and minor grid lines
axes.grid(which='both', alpha=.9)
This provides a semi-log scale probability paper plot! With the nice property that anything plotted on these axes that plots in a straight line indicates that it comes from a normal distribution!



