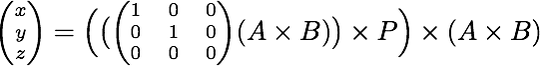get closest point to a line

Question

I'd like to have a straight forward C# function to get a closest point (from a point P) to a line-segment, AB. An abstract function may look like this. I've search through SO but not found a usable (by me) solution.

public Point getClosestPointFromLine(Point A, Point B, Point P);

What do you mean by "to get a closest point (from a point P)"? Do you want the point on the line segment that lies as close as possible to P? — Thomas, Jun 25 '10 at 18:12
Related: [Shortest distance between a point and a line segment](http://stackoverflow.com/questions/849211/shortest-distance-between-a-point-and-a-line-segment) (Not the same.) — Bill the Lizard, Jun 25 '10 at 18:14
Seems to be a point on AB which is on perpendicular from P on AB. — pmod, Jun 25 '10 at 18:16
I want a point on line segment, AB, that is as close as possible to point, P. I believe it is not related to data stored i guess. I saw that relative post, @Bill, but I cannot figure out how to get my requirement from it. — VOX, Jun 25 '10 at 18:24
IT IS NOT HOMEWORK. It's a programmer's question whose maths is bad. — VOX, Jun 25 '10 at 18:25

score 55 · Accepted Answer · edited Mar 01 '16 at 22:50

55

Here's Ruby disguised as Pseudo-Code, assuming Point objects each have a x and y field.

def GetClosestPoint(A, B, P)

  a_to_p = [P.x - A.x, P.y - A.y]     # Storing vector A->P
  a_to_b = [B.x - A.x, B.y - A.y]     # Storing vector A->B

  atb2 = a_to_b[0]**2 + a_to_b[1]**2  # **2 means "squared"
                                      #   Basically finding the squared magnitude
                                      #   of a_to_b

  atp_dot_atb = a_to_p[0]*a_to_b[0] + a_to_p[1]*a_to_b[1]
                                      # The dot product of a_to_p and a_to_b

  t = atp_dot_atb / atb2              # The normalized "distance" from a to
                                      #   your closest point

  return Point.new( :x => A.x + a_to_b[0]*t,
                    :y => A.y + a_to_b[1]*t )
                                      # Add the distance to A, moving
                                      #   towards B

end

Alternatively:

From Line-Line Intersection, at Wikipedia. First, find Q, which is a second point that is to be had from taking a step from P in the "right direction". This gives us four points.

def getClosestPointFromLine(A, B, P)

  a_to_b = [B.x - A.x, B.y - A.y]   # Finding the vector from A to B
                                        This step can be combined with the next
  perpendicular = [ -a_to_b[1], a_to_b[0] ]
                                    # The vector perpendicular to a_to_b;
                                        This step can also be combined with the next

  Q = Point.new(:x => P.x + perpendicular[0], :y => P.y + perpendicular[1])
                                    # Finding Q, the point "in the right direction"
                                    # If you want a mess, you can also combine this
                                    # with the next step.

  return Point.new (:x => ((A.x*B.y - A.y*B.x)*(P.x - Q.x) - (A.x-B.x)*(P.x*Q.y - P.y*Q.x)) / ((A.x - B.x)*(P.y-Q.y) - (A.y - B.y)*(P.y-Q.y)),
                    :y => ((A.x*B.y - A.y*B.x)*(P.y - Q.y) - (A.y-B.y)*(P.x*Q.y - P.y*Q.x)) / ((A.x - B.x)*(P.y-Q.y) - (A.y - B.y)*(P.y-Q.y)) )

end

Caching, Skipping steps, etc. is possible, for performance reasons.

edited Mar 01 '16 at 22:50

Delgan

18,571
11
90
141

answered Jun 26 '10 at 02:54

Justin L.

13,510
5
48
83

3

even though I tagged C# and you answered in ruby, your code works flawlessly. Thanks my friend. – VOX Jul 14 '10 at 16:44
2

@VOX glad to be able to help :) i normally use ruby because it's easy readable and understandable by most people. – Justin L. Jul 14 '10 at 18:24
yeah. I've never learned ruby before but I could easily translate. See you around on next questions. In fact, this is our second meeting. :) – VOX Jul 14 '10 at 19:07
13

a note that the question asked for a line segment, so the parametric value of t should be bounded to [0-1] to be on the segment. – savagepanda Sep 12 '11 at 10:30
1

I am not able to replicate the solution. Does it have anny bounds like only +ve quadrant etc? – user1517108 Jan 12 '13 at 13:25
@user1517108 which one are you attempting? I think it should be able to work everywhere; it's been a while since I wrote it though – Justin L. Jan 12 '13 at 19:55
Attempting the first solution - in javascript but similar logic as described by you. – user1517108 Jan 13 '13 at 05:03
2

SavagePanda is absolutely right. I didn't see his/her comment at first and spent a fair bit of time wondering why my results were not valid points on the line. You MUST clamp T between 0 and 1 for correct output from the function. – Wisteso Mar 11 '15 at 19:59
The Line-Line intersection formula is wrong. The last statement of `getClosestPointFromLine()` should be: `return Point.new (:x => ((A.x*B.y - A.y*B.x)*(P.x - Q.x) - (A.x-B.x)*(P.x*Q.y - P.y*Q.x)) / ((A.x - B.x)*(P.y-Q.y) - (A.y - B.y)*(P.x-Q.x)), :y => ((A.x*B.y - A.y*B.x)*(P.y - Q.y) - (A.y-B.y)*(P.x*Q.y - P.y*Q.x)) / ((A.x - B.x)*(P.y-Q.y) - (A.y - B.y)*(P.x-Q.x)) )` – dubbaluga Sep 19 '16 at 10:28
The Line-Line intersection formula is wrong. The last statement of `getClosestPointFromLine()` should be: `return Point.new (:x => ((A.x*B.y - A.y*B.x)*(P.x - Q.x) - (A.x-B.x)*(P.x*Q.y - P.y*Q.x)) / ((A.x - B.x)*(P.y-Q.y) - (A.y - B.y)*(P.x-Q.x)), :y => ((A.x*B.y - A.y*B.x)*(P.y - Q.y) - (A.y-B.y)*(P.x*Q.y - P.y*Q.x)) / ((A.x - B.x)*(P.y-Q.y) - (A.y - B.y)*(P.x-Q.x)) )` The problem can be found in the very last braced terms of both the x and the y-component of the new point. See: [Wikipedia](https://en.wikipedia.org/wiki/Line%E2%80%93line_intersection#Given_two_points_on_each_line) – dubbaluga Sep 19 '16 at 10:33

score 50 · Answer 2 · answered Mar 04 '12 at 17:39

50

if anyone is interested in a C# XNA function based on the above:

    public static Vector2 GetClosestPointOnLineSegment(Vector2 A, Vector2 B, Vector2 P)
    {
        Vector2 AP = P - A;       //Vector from A to P   
        Vector2 AB = B - A;       //Vector from A to B  

        float magnitudeAB = AB.LengthSquared();     //Magnitude of AB vector (it's length squared)     
        float ABAPproduct = Vector2.Dot(AP, AB);    //The DOT product of a_to_p and a_to_b     
        float distance = ABAPproduct / magnitudeAB; //The normalized "distance" from a to your closest point  

        if (distance < 0)     //Check if P projection is over vectorAB     
        {
            return A;

        }
        else if (distance > 1)             {
            return B;
        }
        else
        {
            return A + AB * distance;
        }
    }

answered Mar 04 '12 at 17:39

N.Schilke

501
4
2

2

+1, this is just slightly better than the answer selected. If you are using this code for checking depth for collision detection, the selected answer will have a nasty push back on both ends, whereas this code doesn't(as far as I've tested). – Shyy Guy Apr 15 '15 at 14:10
3

I know this thread is quite old. However, this solution helped me quite in solving my problem. If you can point me in direction to learn the source or algorithm, which is used in answer, I'd be grateful. I would like to further learn on this regard. – Pasan Ratnayake Jul 18 '16 at 12:00
1

This is better than the accepted answer, IMO, because it is in the correct language. – BrainSlugs83 Feb 18 '21 at 19:01
How Can I use this function ? I have a list of coordinates, So I want to make it to polygon but I got `points must form a closed linestring`I guess I can Use this method but I don't know how can I use this? @BrainSlugs83 – Cyrus the Great May 01 '23 at 13:23

score 13 · Answer 3 · answered Jun 25 '10 at 21:00

Your point (X) will be a linear combination of points A and B:

X = k A + (1-k) B

For X to be actually on the line segment, the parameter k must be between 0 and 1, inclusive. You can compute k as follows:

k_raw = (P-B).(A-B)  /  (A-B).(A-B)

(where the period denotes the dot product)

Then, to make sure the point is actually on the line segment:

if k_raw < 0:
    k= 0
elif k_raw > 1:
    k= 1
else:
    k= k_raw

score 7 · Answer 4 · answered Dec 26 '10 at 23:09

The answer from Justin L. is almost fine, but it doesn't check if the normalized distance is less than 0, or higher than the AB vector magnitude. Then it won't work well when P vector proyection is out of bounds (from the line segment AB). Here's the corrected pseudocode:

    function GetClosestPoint(A, B, P)
{
  vectorAP = (p.x - a.x, p.y - a.y)     //Vector from A to P
  vectorAB = (b.x - a.x, b.y - a.y)     //Vector from A to B

  magnitudeAB = vectorAB[0]^2 + vectorAB[1]^2  
  //Magnitude of AB vector (it's length)


  ABAPproduct = vectorAB[0]*vectorAP[0] + vectorAB[1]*vectorAP[1] 
  //The product of a_to_p and a_to_b


  distance = ABAPproduct / magnitudeAB       
  //The normalized "distance" from a to your closest point

  if ( distance < 0)     //Check if P projection is over vectorAB
    {
        returnPoint.x = a.x
        returnPoint.y = a.y
    }   
  else if (distance > magnitudeAB)
    {
        returnPoint.x = b.x
        returnPoint.y = b.y
    }
  else
    {
        returnPoint.x = a.x + vectorAB[0]*distance
        returnPoint.y = a.y + vectorAB[1]*distance
    }

}

I think this is incorrect, because distance is a normalized distance. You should be comparing distance against 1.0, not (square-of)magnitudeAB. — Matthew Lowe, Sep 20 '12 at 16:31
"else if (distance > magnitudeAB)" should be "else if (distance > 1)" — Vadoff, May 24 '13 at 20:20
Also, the name and comment on magnitudeAB is misleading -- this is a squared magnitude, not the magnitude. — Joe Strout, Feb 11 '14 at 09:17
The correct way to bound distance is by finding if it is less than zero, setting it to zero. And if it is greater than one, setting it to 1. Then you don't need any other changes. In Justin Ls, version if (t > 1) t = 1; if (t < 0) t = 0; --- Only change you need to bound it within the segment. — Tatarize, Jun 20 '15 at 22:20

score 5 · Answer 5 · answered Jul 15 '15 at 10:34

I wrote this a long time ago, it's not much different to what others have said, but it's a copy/paste solution in C# if you have a class (or struct) named PointF with members X and Y:

private static PointF ClosestPointToSegment(PointF P, PointF A, PointF B)
{
    PointF a_to_p = new PointF(), a_to_b = new PointF();
    a_to_p.X = P.X - A.X;
    a_to_p.Y = P.Y - A.Y; //     # Storing vector A->P  
    a_to_b.X = B.X - A.X;
    a_to_b.Y = B.Y - A.Y; //     # Storing vector A->B

    float atb2 = a_to_b.X * a_to_b.X + a_to_b.Y * a_to_b.Y;
    float atp_dot_atb = a_to_p.X * a_to_b.X + a_to_p.Y * a_to_b.Y; // The dot product of a_to_p and a_to_b
    float t = atp_dot_atb / atb2;  //  # The normalized "distance" from a to the closest point
    return new PointF(A.X + a_to_b.X * t, A.Y + a_to_b.Y * t);
}

Update: Looking at the comments it looks like I adapted it to C# from the same source code mentioned in the accepted answer.

as it is, the function returns the closest point on a line that runs trough A and B - add `if (t > 1) t = 1; if (t < 0) t = 0;` to make sure that the point really lies on the segment — Jinjinov, Mar 16 '18 at 14:36

MvG · Answer 6 · 2014-01-13T13:04:59.413

This answer is based on ideas from projective geometry.

Compute the cross product (Ax,Ay,1)×(Bx,By,1)=(u,v,w). The resulting vector describes the line connecting A and B: it has the equation ux+vy+w=0. But you can also interpret (u,v,0) as a point infinitely far away in a direction perpendicular to that line. Doing another cross product you get the line joining hat point to P: (u,v,0)×(Px,Py,1). And to intersect that line with the line AB, you do another cross product: ((u,v,0)×(Px,Py,1))×(u,v,w). The result will be a homogenous coordinate vector (x,y,z) from which you can read the coordinates of this closest point as (x/z,y/z).

Take everything together and you get the following formula:

${\scriptsize\begin{pmatrix}x\y\z\end{pmatrix}}=\Bigl(\bigl({\scriptsize\begin{pmatrix}1&0&0\0&1&0\0&0&0\end{pmatrix}}(A\times B)\bigr)\times P\Bigr)\times(A\times B)$

Using a computer algebra system, you can find the resulting coordinates to be the following:

x = ((Ax - Bx)*Px + (Ay - By)*Py)*(Ax - Bx) + (Ay*Bx - Ax*By)*(Ay - By)
y = -(Ay*Bx - Ax*By)*(Ax - Bx) + ((Ax - Bx)*Px + (Ay - By)*Py)*(Ay - By)
z = (Ax - Bx)^2 + (Ay - By)^2

As you notice, there are a lot of recurring terms. Inventing (pretty much arbitrary) names for these, you can get the following final result, written in pseudocode:

dx = A.x - B.x
dy = A.y - B.y
det = A.y*B.x - A.x*B.y
dot = dx*P.x + dy*P.y
x = dot*dx + det*dy
y = dot*dy - det*dx
z = dx*dx + dy*dy
zinv = 1/z
return new Point(x*zinv, y*zinv)

Benefits of this approach:

No case distinctions
No square roots
Only a single division

@mtourne: If you omit that diagonal matrix, you're using elliptic geometry not Euclidean. I think I had a post somewhere (here or on MSE) about the spherical version of this problem, but I can't seem to find it just now. In any case, for A=(1,2,1),B=(3,5,1),P=(7,6,1) you get (68, 104, 4)∼(884, 1352, 52) but I get (61, 98, 13)∼(244, 392, 52). So they are not equal. — MvG, Apr 09 '14 at 07:14

Amadan · Answer 7 · 2010-06-28T05:22:20.337

4

Find the slope a1 of AB by dividing the y-difference with the x-difference; then draw a perpendicular line (with slope a2 = -1/a1, you need to solve for the offset (b2) by putting P's coordinates into y = a2*x + b2); then you have two lines (i.e. two linear equations), and you need to solve the intersection. That will be your closest point.

Do the math right, and the function will be pretty trivial to write.

To elaborate a bit:

Original line:
y = a1 * x + b1
a1 = (By - Ay) / (Bx - Ax)   <--
b1 = Ay - a1 * Ax            <--

Perpendicular line:
y = a2 * x + b2
a2 = -1/a1                   <--
b2 = Py - a2 * Px            <--

Now you have P which lies on both lines:
y = a1 * x + b1
y = a2 * x + b2
--------------- subtract:
0 = (a1 - a2) * Px + (b1 - b2)
x = - (b1 - b2) / (a1 - a2)  <--
y = a1 * x + b1              <--

Hope I didn't mess up somewhere :) UPDATE Of course I did. Serve me right for not working things out on paper first. I deserved every downvote, but I'd've expected someone to correct me. Fixed (I hope).

Arrows point the way.

UPDATE Ah, the corner cases. Yeah, some languages don't handle infinities well. I did say the solution was language-free...

You can check the special cases, they're quite easy. The first one is when the x difference is 0. That means the line is vertical, and the closest point is on a horizontal perpendicular. Thus, x = Ax, y = Px.

The second one is when y difference is 0, and the opposite is true. Thus, x = Px, y = Ay

edited Jun 28 '10 at 05:22

answered Jun 25 '10 at 18:21

Amadan

191,408
23
240
301

I'm bad in math. too bad I could not reproduce a function from what you are telling me, thanks you anyway. :( – VOX Jun 25 '10 at 18:27
All right, I spelled it out for you - just hope I still have it :D – Amadan Jun 25 '10 at 18:29
@Amadan, I'm still in bad math. :( I guess yours isn't C# code but maths equations and they're not in top-bottom order? I'm confused. Thanks again. – VOX Jun 25 '10 at 18:50
Okay - the lines with arrows are pretty much executable code (just be sure to translate to C# idiom by replacing `Py` with `P.Y`, add proper declarations and the like). – Amadan Jun 25 '10 at 19:04
1

Your function (the first line) gave me error when Ax and Bx are equal. DivitionByZero exception was thrown when the line is vertical. – VOX Jun 25 '10 at 22:01
I find dealing with slopes to be pretty dangerous overall, when programming. – Justin L. Jun 26 '10 at 02:42
@Amadan, your solution have some problems. Sometimes, its correct, manytimes, it show wrong results. – VOX Jul 14 '10 at 16:43

score 2 · Answer 8 · answered Apr 15 '16 at 21:00

Here are extension methods that should do the trick:

public static double DistanceTo(this Point from, Point to)
    {
        return Math.Sqrt(Math.Pow(from.X - to.X, 2) + Math.Pow(from.Y - to.Y, 2));
    }

public static double DistanceTo(this Point point, Point lineStart, Point lineEnd)
    {
        double tI = ((lineEnd.X - lineStart.X) * (point.X - lineStart.X) + (lineEnd.Y - lineStart.Y) * (point.Y - lineStart.Y)) / Math.Pow(lineStart.DistanceTo(lineEnd), 2);
        double dP = ((lineEnd.X - lineStart.X) * (point.Y - lineStart.Y) - (lineEnd.Y - lineStart.Y) * (point.X - lineStart.X)) / lineStart.DistanceTo(lineEnd);

        if (tI >= 0d && tI <= 1d)
            return Math.Abs(dP);
        else
            return Math.Min(point.DistanceTo(lineStart), point.DistanceTo(lineEnd));
    }

Then just call:

P.DistanceTo(A, B);

To get distance of point "P" from line |AB|. It should be easy to modify this for PointF.

Finding the closest point then is just a matter of searching minimal distance. LINQ has methods for this.

score 1 · Answer 9 · answered Jun 25 '10 at 18:21

The closest point C will be on a line whose slope is the reciprocal of AB and which intersects with P. This sounds like it might be homework, but I'll give some pretty strong hints, in order of increasing spoiler-alert level:

There can be only one such line.
This is a system of two line equations. Just solve for x and y.
Draw a line segment between A and B; call this L. The equation for L is y = mx + b, where m is the ratio of the y-coordinates to the x-coordinates. Solve for b using either A or B in the expression.
Do the same as above, but for CP. Now solve the simultaneous linear system of equations.
A Google search will give you a bevy of examples to choose from.

score 0 · Answer 10 · answered Jun 03 '14 at 22:12

0

In case somebody is looking for a way to do this with Java + LibGdx:

Intersector.nearestSegmentPoint

answered Jun 03 '14 at 22:12

Nick Bilyk

352
2
8

score 0 · Answer 11 · answered Jan 24 '20 at 13:32

This is the right algorythm to get nearest point of a segment from a point(Tested)(vb.net)

s2 = ClosestPointToSegment(point_x, Point_y, Segment_start_x, Segment_start_y, Segment_end_X, Segment_end_Y)

Public Shared Function DistanceTo(x1 As Double, y1 As Double, x2 As Double, y2 As Double) As Double
    Return Math.Sqrt(Math.Pow(x1 - x2, 2) + Math.Pow(y1 - y2, 2))
End Function


Public Shared Function DistanceTo(point_x As Double, point_y As Double, lineStart_x As Double, lineStart_y As Double, lineEnd_x As Double, lineEnd_y As Double) As Double
    Dim tI As Double = ((lineEnd_x - lineStart_x) * (point_x - lineStart_x) + (lineEnd_y - lineStart_y) * (point_y - lineStart_x)) / Math.Pow(DistanceTo(lineStart_x, lineStart_y, lineEnd_x, lineEnd_y), 2)
    Dim dP As Double = ((lineEnd_x - lineStart_x) * (point_y - lineStart_y) - (lineEnd_y - lineStart_y) * (point_x - lineStart_x)) / DistanceTo(lineStart_x, lineStart_y, lineEnd_x, lineEnd_y)

    If tI >= 0R AndAlso tI <= 1.0R Then
        Return Math.Abs(dP)
    Else
        Return Math.Min(DistanceTo(point_x, point_y, lineStart_x, lineStart_y), DistanceTo(point_x, point_y, lineEnd_x, lineEnd_y))
    End If
End Function
Private Shared Function ClosestPointToSegment(P_x As Double, p_y As Double, A_x As Double, a_y As Double, B_x As Double, b_y As Double) As Double()
    Dim a_to_p As PointF = New PointF(), a_to_b As PointF = New PointF()
    Dim rikthex As Double, rikthey As Double
    Dim s1(1) As Double
    Dim p1_v1_X As Double, p1_v1_y As Double, distanca1 As Double, distanca2 As Double
    a_to_p.X = P_x - A_x
    a_to_p.Y = p_y - a_y
    a_to_b.X = B_x - A_x
    a_to_b.Y = b_y - a_y
    Dim atb2 As Single = a_to_b.X * a_to_b.X + a_to_b.Y * a_to_b.Y
    Dim atp_dot_atb As Single = a_to_p.X * a_to_b.X + a_to_p.Y * a_to_b.Y
    Dim t As Single = atp_dot_atb / atb2
    rikthex = A_x + a_to_b.X * t
    rikthey = a_y + a_to_b.Y * t
    If A_x > B_x Then
        If rikthex < A_x And rikthex > B_x Then 'pika duhet ne rregulll
            If a_y > b_y Then
                If rikthey < a_y And rikthey > b_y Then 'pika duhet ne rregulll

                Else
                    distanca1 = DistanceTo(P_x, p_y, A_x, a_y)
                    distanca2 = DistanceTo(P_x, p_y, B_x, b_y)
                    If distanca1 < distanca2 Then
                        rikthex = A_x
                        rikthey = a_y
                    Else
                        rikthex = B_x
                        rikthey = b_y
                    End If

                End If
            Else
                If rikthey > a_y And rikthey < b_y Then 'pika duhet ne rregulll

                Else
                    distanca1 = DistanceTo(P_x, p_y, A_x, a_y)
                    distanca2 = DistanceTo(P_x, p_y, B_x, b_y)
                    If distanca1 < distanca2 Then
                        rikthex = A_x
                        rikthey = a_y
                    Else
                        rikthex = B_x
                        rikthey = b_y
                    End If

                End If

            End If
        Else
            distanca1 = DistanceTo(P_x, p_y, A_x, a_y)
            distanca2 = DistanceTo(P_x, p_y, B_x, b_y)
            If distanca1 < distanca2 Then
                rikthex = A_x
                rikthey = a_y
            Else
                rikthex = B_x
                rikthey = b_y
            End If
        End If
    Else
        If rikthex > A_x And rikthex < B_x Then 'pika duhet ne rregulll
            If a_y > b_y Then
                If rikthey < a_y And rikthey > b_y Then 'pika duhet ne rregulll

                Else
                    distanca1 = DistanceTo(P_x, p_y, A_x, a_y)
                    distanca2 = DistanceTo(P_x, p_y, B_x, b_y)
                    If distanca1 < distanca2 Then
                        rikthex = A_x
                        rikthey = a_y
                    Else
                        rikthex = B_x
                        rikthey = b_y
                    End If

                End If
            Else
                If rikthey > a_y And rikthey < b_y Then 'pika duhet ne rregulll

                Else
                    distanca1 = DistanceTo(P_x, p_y, A_x, a_y)
                    distanca2 = DistanceTo(P_x, p_y, B_x, b_y)
                    If distanca1 < distanca2 Then
                        rikthex = A_x
                        rikthey = a_y
                    Else
                        rikthex = B_x
                        rikthey = b_y
                    End If

                End If

            End If
        Else
            distanca1 = DistanceTo(P_x, p_y, A_x, a_y)
            distanca2 = DistanceTo(P_x, p_y, B_x, b_y)
            If distanca1 < distanca2 Then
                rikthex = A_x
                rikthey = a_y
            Else
                rikthex = B_x
                rikthey = b_y
            End If
        End If
    End If
    s1(0) = rikthex
    s1(1) = rikthey
    Return s1

End Function

score 0 · Answer 12 · answered Jul 27 '21 at 07:03

In case anybody looking for python implementation, here is the code:

p1 and p2 is line, p3 is the point

def p4(p1, p2, p3):
     x1, y1 = p1
     x2, y2 = p2
     x3, y3 = p3
     dx, dy = x2-x1, y2-y1
     det = dx*dx + dy*dy
     a = (dy*(y3-y1)+dx*(x3-x1))/det
     x= x1+a*dx, y1+a*dy
     # print(x)
     if x[0]<x1 or x[1]<y1:
         return p1
     elif x[0]>x2 or x[1]>y2:
         return p2
     else:
         return x

This was taken from another thread and modified a little. Python: point on a line closest to third point

score -3 · Answer 13 · answered Jun 25 '10 at 18:17

-3

The algorithm would be quite easy:

you have 3 points - triangle. From there you should be able to find AB, AC, BC.

Theck this out: http://www.topcoder.com/tc?d1=tutorials&d2=geometry1&module=Static#line_point_distance

answered Jun 25 '10 at 18:17

Ryan Ternier

8,714
4
46
69

get closest point to a line

13 Answers13

Linked

Related