I am trying to create a color wheel in Python, preferably using Matplotlib. The following works OK:
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
xval = np.arange(0, 2*pi, 0.01)
yval = np.ones_like(xval)
colormap = plt.get_cmap('hsv')
norm = mpl.colors.Normalize(0.0, 2*np.pi)
ax = plt.subplot(1, 1, 1, polar=True)
ax.scatter(xval, yval, c=xval, s=300, cmap=colormap, norm=norm, linewidths=0)
ax.set_yticks([])
However, this attempt has two serious drawbacks.
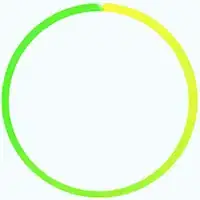
First, when saving the resulting figure as a vector (figure_1.svg), the color wheel consists (as expected) of 621 different shapes, corresponding to the different (x,y) values being plotted. Although the result looks like a circle, it isn't really. I would greatly prefer to use an actual circle, defined by a few path points and Bezier curves between them, as in e.g. matplotlib.patches.Circle. This seems to me the 'proper' way of doing it, and the result would look nicer (no banding, better gradient, better anti-aliasing).
Second (relatedly), the final plotted markers (the last few before 2*pi) overlap the first few. It's very hard to see in the pixel rendering, but if you zoom in on the vector-based rendering you can clearly see the last disc overlap the first few.
I tried using different markers (. or |), but none of them go around the second issue.
Bottom line: can I draw a circle in Python/Matplotlib which is defined in the proper vector/Bezier curve way, and which has an edge color defined according to a colormap (or, failing that, an arbitrary color gradient)?