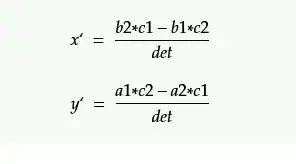How would I use numpy to calculate the intersection between two line segments?
In the code I have segment1 = ((x1,y1),(x2,y2)) and segment2 = ((x1,y1),(x2,y2)). Note segment1 does not equal segment2. So in my code I've also been calculating the slope and y-intercept, it would be nice if that could be avoided but I don't know of a way how.
I've been using Cramer's rule with a function I wrote up in Python but I'd like to find a faster way of doing this.
Stolen directly from https://web.archive.org/web/20111108065352/https://www.cs.mun.ca/~rod/2500/notes/numpy-arrays/numpy-arrays.html
#
# line segment intersection using vectors
# see Computer Graphics by F.S. Hill
#
from numpy import *
def perp( a ) :
b = empty_like(a)
b[0] = -a[1]
b[1] = a[0]
return b
# line segment a given by endpoints a1, a2
# line segment b given by endpoints b1, b2
# return
def seg_intersect(a1,a2, b1,b2) :
da = a2-a1
db = b2-b1
dp = a1-b1
dap = perp(da)
denom = dot( dap, db)
num = dot( dap, dp )
return (num / denom.astype(float))*db + b1
p1 = array( [0.0, 0.0] )
p2 = array( [1.0, 0.0] )
p3 = array( [4.0, -5.0] )
p4 = array( [4.0, 2.0] )
print seg_intersect( p1,p2, p3,p4)
p1 = array( [2.0, 2.0] )
p2 = array( [4.0, 3.0] )
p3 = array( [6.0, 0.0] )
p4 = array( [6.0, 3.0] )
print seg_intersect( p1,p2, p3,p4)
import numpy as np
def get_intersect(a1, a2, b1, b2):
"""
Returns the point of intersection of the lines passing through a2,a1 and b2,b1.
a1: [x, y] a point on the first line
a2: [x, y] another point on the first line
b1: [x, y] a point on the second line
b2: [x, y] another point on the second line
"""
s = np.vstack([a1,a2,b1,b2]) # s for stacked
h = np.hstack((s, np.ones((4, 1)))) # h for homogeneous
l1 = np.cross(h[0], h[1]) # get first line
l2 = np.cross(h[2], h[3]) # get second line
x, y, z = np.cross(l1, l2) # point of intersection
if z == 0: # lines are parallel
return (float('inf'), float('inf'))
return (x/z, y/z)
if __name__ == "__main__":
print get_intersect((0, 1), (0, 2), (1, 10), (1, 9)) # parallel lines
print get_intersect((0, 1), (0, 2), (1, 10), (2, 10)) # vertical and horizontal lines
print get_intersect((0, 1), (1, 2), (0, 10), (1, 9)) # another line for fun
Note that the equation of a line is ax+by+c=0. So if a point is on this line, then it is a solution to (a,b,c).(x,y,1)=0 (. is the dot product)
let l1=(a1,b1,c1), l2=(a2,b2,c2) be two lines and p1=(x1,y1,1), p2=(x2,y2,1) be two points.
let t=p1xp2 (the cross product of two points) be a vector representing a line.
We know that p1 is on the line t because t.p1 = (p1xp2).p1=0.
We also know that p2 is on t because t.p2 = (p1xp2).p2=0. So t must be the line passing through p1 and p2.
This means that we can get the vector representation of a line by taking the cross product of two points on that line.
Now let r=l1xl2 (the cross product of two lines) be a vector representing a point
We know r lies on l1 because r.l1=(l1xl2).l1=0. We also know r lies on l2 because r.l2=(l1xl2).l2=0. So r must be the point of intersection of the lines l1 and l2.
Interestingly, we can find the point of intersection by taking the cross product of two lines.
This is is a late response, perhaps, but it was the first hit when I Googled 'numpy line intersections'. In my case, I have two lines in a plane, and I wanted to quickly get any intersections between them, and Hamish's solution would be slow -- requiring a nested for loop over all line segments.
Here's how to do it without a for loop (it's quite fast):
from numpy import where, dstack, diff, meshgrid
def find_intersections(A, B):
# min, max and all for arrays
amin = lambda x1, x2: where(x1<x2, x1, x2)
amax = lambda x1, x2: where(x1>x2, x1, x2)
aall = lambda abools: dstack(abools).all(axis=2)
slope = lambda line: (lambda d: d[:,1]/d[:,0])(diff(line, axis=0))
x11, x21 = meshgrid(A[:-1, 0], B[:-1, 0])
x12, x22 = meshgrid(A[1:, 0], B[1:, 0])
y11, y21 = meshgrid(A[:-1, 1], B[:-1, 1])
y12, y22 = meshgrid(A[1:, 1], B[1:, 1])
m1, m2 = meshgrid(slope(A), slope(B))
m1inv, m2inv = 1/m1, 1/m2
yi = (m1*(x21-x11-m2inv*y21) + y11)/(1 - m1*m2inv)
xi = (yi - y21)*m2inv + x21
xconds = (amin(x11, x12) < xi, xi <= amax(x11, x12),
amin(x21, x22) < xi, xi <= amax(x21, x22) )
yconds = (amin(y11, y12) < yi, yi <= amax(y11, y12),
amin(y21, y22) < yi, yi <= amax(y21, y22) )
return xi[aall(xconds)], yi[aall(yconds)]
Then to use it, provide two lines as arguments, where is arg is a 2 column matrix, each row corresponding to an (x, y) point:
# example from matplotlib contour plots
Acs = contour(...)
Bsc = contour(...)
# A and B are the two lines, each is a
# two column matrix
A = Acs.collections[0].get_paths()[0].vertices
B = Bcs.collections[0].get_paths()[0].vertices
# do it
x, y = find_intersections(A, B)
have fun
This is a version of @Hamish Grubijan's answer that also works for multiple points in each of the input arguments, i.e., a1, a2, b1, b2 can be Nx2 row arrays of 2D points. The perp function is replaced by a dot product.
T = np.array([[0, -1], [1, 0]])
def line_intersect(a1, a2, b1, b2):
da = np.atleast_2d(a2 - a1)
db = np.atleast_2d(b2 - b1)
dp = np.atleast_2d(a1 - b1)
dap = np.dot(da, T)
denom = np.sum(dap * db, axis=1)
num = np.sum(dap * dp, axis=1)
return np.atleast_2d(num / denom).T * db + b1
I would like to add something small here. The original question is about line segments. I arrived here, because I was looking for line segment intersection, which in my case meant that I need to filter those cases, where no intersection of the line segments exists. Here is some code which does that:
def line_intersection(x1, y1, x2, y2, x3, y3, x4, y4):
"""find the intersection of line segments A=(x1,y1)/(x2,y2) and
B=(x3,y3)/(x4,y4). Returns a point or None"""
denom = ((x1 - x2) * (y3 - y4) - (y1 - y2) * (x3 - x4))
if denom==0: return None
px = ((x1 * y2 - y1 * x2) * (x3 - x4) - (x1 - x2) * (x3 * y4 - y3 * x4)) / denom
py = ((x1 * y2 - y1 * x2) * (y3 - y4) - (y1 - y2) * (x3 * y4 - y3 * x4)) / denom
if (px - x1) * (px - x2) < 0 and (py - y1) * (py - y2) < 0 \
and (px - x3) * (px - x4) < 0 and (py - y3) * (py - y4) < 0:
return [px, py]
else:
return None
In case you are looking for a vectorized version where we can rule out vertical line segments.
def intersect(a):
# a numpy array with dimension [n, 2, 2, 2]
# axis 0: line-pair, axis 1: two lines, axis 2: line delimiters axis 3: x and y coords
# for each of the n line pairs a boolean is returned stating of the two lines intersect
# Note: the edge case of a vertical line is not handled.
m = (a[:, :, 1, 1] - a[:, :, 0, 1]) / (a[:, :, 1, 0] - a[:, :, 0, 0])
t = a[:, :, 0, 1] - m[:, :] * a[:, :, 0, 0]
x = (t[:, 0] - t[:, 1]) / (m[:, 1] - m[:, 0])
y = m[:, 0] * x + t[:, 0]
r = a.min(axis=2).max(axis=1), a.max(axis=2).min(axis=1)
return (x >= r[0][:, 0]) & (x <= r[1][:, 0]) & (y >= r[0][:, 1]) & (y <= r[1][:, 1])
A sample invocation would be:
intersect(np.array([
[[[1, 2], [2, 2]],
[[1, 2], [1, 1]]], # I
[[[3, 4], [4, 4]],
[[4, 4], [5, 6]]], # II
[[[2, 0], [3, 1]],
[[3, 0], [4, 1]]], # III
[[[0, 5], [2, 5]],
[[2, 4], [1, 3]]], # IV
]))
# returns [False, True, False, False]
Visualization (I need more reputation to post images here).
Here's a (bit forced) one-liner:
import numpy as np
from scipy.interpolate import interp1d
x = np.array([0, 1])
segment1 = np.array([0, 1])
segment2 = np.array([-1, 2])
x_intersection = interp1d(segment1 - segment2, x)(0)
# if you need it:
y_intersection = interp1d(x, segment1)(x_intersection)
Interpolate the difference (default is linear), and find a 0 of the inverse.
Cheers!
This is what I use to find line intersection, it works having either 2 points of each line, or just a point and its slope. I basically solve the system of linear equations.
def line_intersect(p0, p1, m0=None, m1=None, q0=None, q1=None):
''' intersect 2 lines given 2 points and (either associated slopes or one extra point)
Inputs:
p0 - first point of first line [x,y]
p1 - fist point of second line [x,y]
m0 - slope of first line
m1 - slope of second line
q0 - second point of first line [x,y]
q1 - second point of second line [x,y]
'''
if m0 is None:
if q0 is None:
raise ValueError('either m0 or q0 is needed')
dy = q0[1] - p0[1]
dx = q0[0] - p0[0]
lhs0 = [-dy, dx]
rhs0 = p0[1] * dx - dy * p0[0]
else:
lhs0 = [-m0, 1]
rhs0 = p0[1] - m0 * p0[0]
if m1 is None:
if q1 is None:
raise ValueError('either m1 or q1 is needed')
dy = q1[1] - p1[1]
dx = q1[0] - p1[0]
lhs1 = [-dy, dx]
rhs1 = p1[1] * dx - dy * p1[0]
else:
lhs1 = [-m1, 1]
rhs1 = p1[1] - m1 * p1[0]
a = np.array([lhs0,
lhs1])
b = np.array([rhs0,
rhs1])
try:
px = np.linalg.solve(a, b)
except:
px = np.array([np.nan, np.nan])
return px
To solve this, we have to convert our lines to the following form: ax+by=c. where
a = y1 - y2
b = x1 - x2
c = ax1 + by1
If we apply this equation for each line, we will got two line equation. a1x+b1y=c1 and a2x+b2y=c2.
Now when we got the expression for both lines.
First of all we have to check if the lines are parallel or not. To examine this we want to find the determinant. The lines are parallel if the determinant is equal to zero.
We find the determinant by solving the following expression:
det = a1 * b2 - a2 * b1
If the determinant is equal to zero, then the lines are parallel and will never intersect. If the lines are not parallel, they must intersect at some point.
The point of the lines intersects are found using the following formula:
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
'''
finding intersect point of line AB and CD
where A is the first point of line AB
and B is the second point of line AB
and C is the first point of line CD
and D is the second point of line CD
'''
def get_intersect(A, B, C, D):
# a1x + b1y = c1
a1 = B.y - A.y
b1 = A.x - B.x
c1 = a1 * (A.x) + b1 * (A.y)
# a2x + b2y = c2
a2 = D.y - C.y
b2 = C.x - D.x
c2 = a2 * (C.x) + b2 * (C.y)
# determinant
det = a1 * b2 - a2 * b1
# parallel line
if det == 0:
return (float('inf'), float('inf'))
# intersect point(x,y)
x = ((b2 * c1) - (b1 * c2)) / det
y = ((a1 * c2) - (a2 * c1)) / det
return (x, y)
I wrote a module for line to compute this and some other simple line operations. It is implemented in c++, so it works very fast. You can install FastLine via pip and then use it in this way:
from FastLine import Line
# define a line by two points
l1 = Line(p1=(0,0), p2=(10,10))
# or define a line by slope and intercept
l2 = Line(m=0.5, b=-1)
# compute intersection
p = l1.intersection(l2)
# returns (-2.0, -2.0)
The reason you would want to use numpy code is because it's faster and it's only really faster when you can broadcast it. The way you make numpy code fast is by doing everything in a series of of numpy operations without loops. If you're not going to do this, don't use numpy.
def line_intersect(x1, y1, x2, y2, x3, y3, x4, y4):
denom = (y4 - y3) * (x2 - x1) - (x4 - x3) * (y2 - y1)
if denom == 0:
return None # Parallel.
ua = ((x4 - x3) * (y1 - y3) - (y4 - y3) * (x1 - x3)) / denom
ub = ((x2 - x1) * (y1 - y3) - (y2 - y1) * (x1 - x3)) / denom
if 0.0 <= ua <= 1.0 and 0.0 <= ub <= 1.0:
return (x1 + ua * (x2 - x1)), (y1 + ua * (y2 - y1))
return None
However, let's do use numpy:
It's a bit easier to deal with points as complex numbers (x=real, y=imag). That trick is used elsewhere. And rather than a 2d set of elements we use a numpy 1d complex array for the 2d points.
import numpy as np
def find_intersections(a, b):
old_np_seterr = np.seterr(divide="ignore", invalid="ignore")
try:
ax1, bx1 = np.meshgrid(np.real(a[:-1]), np.real(b[:-1]))
ax2, bx2 = np.meshgrid(np.real(a[1:]), np.real(b[1:]))
ay1, by1 = np.meshgrid(np.imag(a[:-1]), np.imag(b[:-1]))
ay2, by2 = np.meshgrid(np.imag(a[1:]), np.imag(b[1:]))
# Note if denom is zero these are parallel lines.
denom = (by2 - by1) * (ax2 - ax1) - (bx2 - bx1) * (ay2 - ay1)
ua = ((bx2 - bx1) * (ay1 - by1) - (by2 - by1) * (ax1 - bx1)) / denom
ub = ((ax2 - ax1) * (ay1 - by1) - (ay2 - ay1) * (ax1 - bx1)) / denom
hit = np.dstack((0.0 <= ua, ua <= 1.0, 0.0 <= ub, ub <= 1.0)).all(axis=2)
ax1 = ax1[hit]
ay1 = ay1[hit]
x_vals = ax1 + ua[hit] * (ax2[hit] - ax1)
y_vals = ay1 + ua[hit] * (ay2[hit] - ay1)
return x_vals + y_vals * 1j
finally:
np.seterr(**old_np_seterr)
Invoking code:
import svgelements as svge
from random import random
import numpy as np
j = svge.Path(svge.Circle(cx=random() * 5, cy=random() * 5, r=random() * 5)).npoint(
np.arange(0, 1, 0.001)
)
k = svge.Path(svge.Circle(cx=random() * 5, cy=random() * 5, r=random() * 5)).npoint(
np.arange(0, 1, 0.001)
)
j = j[:, 0] + j[:, 1] * 1j
k = k[:, 0] + k[:, 1] * 1j
intersects = find_intersections(j, k)
print(intersects)
# Random circles will intersect in 0 or 2 points.
In our code, a and b are segment lists. These expect to be a series of connected points and we mesh them to find any segment n -> n+1 segment that intersects with any or all the other segments.
We return all intersections between the polyline a and the polyline b.
Two tricks (for adaptations):
We mesh all the segments. We check every segment in the polyline a list and every segment in the polyline b list. It's pretty easy to see how you'd arrange this if you wanted other inputs.
Many code examples will check if denom is zero but that's not allowed in pure array code since there's a mesh of different points to check, so conditionals need to be in-lined. We turn off the seterr for dividing by 0 and infinity because we expect to do that if we have parallel lines. Which gets rid of the check for denom being zero. If denom is zero then the lines are parallel which means they either meet at 0 points or infinite many points. The typical conditional checking for the values of ua and ub is done in an array stack of each of the checks which then sees if all of these are true for any elements, and then just returns true for those elements.
If you need the value t or the segments within the lists that intersected this should be readily determined from the ua ub and hit.
import numpy as np
data = np.array([
# segment1 segment2
# [[x1, y1], [x2, y2]], [[x1, y1], [x2, y2]]
[[0, 0], [1, 1], [0, 1], [1, 0]],
[[0, 0], [1, 1], [1, 0], [1, 1]],
[(0, 1), (0, 2), (1, 10), (2, 10)],
[(0, 1), (1, 2), (0, 10), (1, 9)],
[[0, 0], [0, 1], [0, 2], [1, 3]],
[[0, 1], [2, 3], [4, 5], [6, 7]],
[[1, 2], [3, 4], [5, 6], [7, 8]]
])
def intersect(data):
L = len(data)
x1, y1, x2, y2 = data.reshape(L * 2, -1).T
R = np.full([L, 2], np.nan)
X = np.concatenate([
(y2 - y1).reshape(L * 2, -1),
(x1 - x2).reshape(L * 2, -1)],
axis=1
).reshape(L, 2, 2)
B = (x1 * y2 - x2 * y1).reshape(L, 2)
I = np.isfinite(np.linalg.cond(X))
R[I] = np.matmul(np.linalg.inv(X[I]), B[I][:,:,None]).squeeze(-1)
return R
intersect(data)
array([[ 0.5, 0.5],
[ 1. , 1. ],
[ 0. , 10. ],
[ 4.5, 5.5],
[ 0. , 2. ],
[ nan, nan],
[ nan, nan]])
