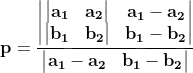How do I compute the intersection point of two lines?

Question

I have two lines that intersect at a point. I know the endpoints of the two lines. How do I compute the intersection point in Python?

# Given these endpoints
#line 1
A = [X, Y]
B = [X, Y]

#line 2
C = [X, Y]
D = [X, Y]

# Compute this:
point_of_intersection = [X, Y]

This problem mostly boils down to "do the math". You can use algebraic manipulation to find an expression for the coordinates of the intersection, then insert that expression into your program. Remember to check for parallel lines first, though. — user2357112, Dec 19 '13 at 09:33
Search stackoverflow before ask a question : [the answer][1] [1]: http://stackoverflow.com/questions/3252194/numpy-and-line-intersections — Cao Manh Dat, Dec 19 '13 at 09:33
*“I know how to do this on paper”* — Then what exactly is your problem? It’s pure math which you need to apply here. And Python is your calculator. What have you tried? — poke, Dec 19 '13 at 09:34
possible duplicate of [How can I check if two segments intersect?](http://stackoverflow.com/questions/3838329/how-can-i-check-if-two-segments-intersect) — Jerry Coffin, Dec 19 '13 at 09:43

Paul Draper · Accepted Answer · 2019-05-26T06:24:15.430

103

Unlike other suggestions, this is short and doesn't use external libraries like numpy. (Not that using other libraries is bad...it's nice not need to, especially for such a simple problem.)

def line_intersection(line1, line2):
    xdiff = (line1[0][0] - line1[1][0], line2[0][0] - line2[1][0])
    ydiff = (line1[0][1] - line1[1][1], line2[0][1] - line2[1][1])

    def det(a, b):
        return a[0] * b[1] - a[1] * b[0]

    div = det(xdiff, ydiff)
    if div == 0:
       raise Exception('lines do not intersect')

    d = (det(*line1), det(*line2))
    x = det(d, xdiff) / div
    y = det(d, ydiff) / div
    return x, y

print line_intersection((A, B), (C, D))

And FYI, I would use tuples instead of lists for your points. E.g.

A = (X, Y)

EDIT: Initially there was a typo. That was fixed Sept 2014 thanks to @zidik.

This is simply the Python transliteration of the following formula, where the lines are (a1, a2) and (b1, b2) and the intersection is p. (If the denominator is zero, the lines have no unique intersection.)

edited May 26 '19 at 06:24

answered Dec 19 '13 at 09:38

Paul Draper

78,542
46
206
285

7

This solution yields (1.0, 2.0) for intersecting `line_intersection(((0.5, 0.5), (1.5, 0.5)), ((1, 0), (1, 2)))`, which should be (1, 0.5). – xtofl Aug 11 '14 at 01:14
5

I have to agree with @xtofl - this doesn't work. I get false positives and negatives. – rbaleksandar Sep 08 '16 at 12:57
2

Î would also avoid using exceptions here. A simple `False` would do and it's not as expensive as handling an exception. – rbaleksandar Sep 08 '16 at 13:12
This solution doesn't work for points that intersect at (0.,0.) – Lee Feb 23 '17 at 15:58
1

Ha! @Pithikos was about to say that... Reinventing the wheel is only good for learning/understanding and never for implementing – user32882 Mar 17 '19 at 15:08
I would **never** implement code that is already programmed in a library: that is time wasting and you undergo the risk of make a buggy code. As @user32882 said, the only sense of self implementing is to learn—but that was not the question. I recommend this answer for the [mathematics forum](https://math.stackexchange.com/). ;) – loved.by.Jesus Sep 29 '20 at 15:21
1

@loved.by.Jesus I agree. As long as you have a good way of installing, auditing, deploying, and updating your library. – Paul Draper Sep 29 '20 at 16:38
"using other libraries is bad" what?? but numpy is widely used, and implementation is much nicer https://stackoverflow.com/a/42727584/2580835 – iperov Mar 13 '21 at 05:57
@rbaleksandar, I would disagree. Using an exception is the way to go based on the return type of the function. Just because Python allows a function to return multiple types doesn't mean you should. – ubiquibacon Mar 24 '22 at 20:39
As others have noted, this is giving false positives. These lines for instance `((0.5, 0.5), (1.0, 0.5))` and `((0.7471, 0.2936), (0.751, 0.25))` do not intersect. We can easily see that when the lines are graphed, yet the function claims they intersect at '(0.7286376146788988, 0.5`. – ubiquibacon Mar 24 '22 at 21:16
Great! I also tested it in graphics. The intersection point was exact! (And I totally agree: avoiding importing modules is always better. It requires more skills.) – Apostolos Dec 29 '22 at 19:01
@iperov, but maybe you would like to use PyPy. There are implicit decisions/complications. No bad, but not non-existent either. – Paul Draper Jan 30 '23 at 05:09

score 88 · Answer 2 · answered Dec 19 '13 at 10:46

88

Can't stand aside,

So we have linear system:

A₁ * x + B₁ * y = C₁
A₂ * x + B₂ * y = C₂

let's do it with Cramer's rule, so solution can be found in determinants:

x = D_x/D
y = D_y/D

where D is main determinant of the system:

A₁ B₁
A₂ B₂

and D_x and D_y can be found from matricies:

C₁ B₁
C₂ B₂

and

A₁ C₁
A₂ C₂

(notice, as C column consequently substitues the coef. columns of x and y)

So now the python, for clarity for us, to not mess things up let's do mapping between math and python. We will use array L for storing our coefs A, B, C of the line equations and intestead of pretty x, y we'll have [0], [1], but anyway. Thus, what I wrote above will have the following form further in the code:

for D

L1[0] L1[1]
L2[0] L2[1]

for D_x

L1[2] L1[1]
L2[2] L2[1]

for D_y

L1[0] L1[2]
L2[0] L2[2]

Now go for coding:

line - produces coefs A, B, C of line equation by two points provided,
intersection - finds intersection point (if any) of two lines provided by coefs.

from __future__ import division 

def line(p1, p2):
    A = (p1[1] - p2[1])
    B = (p2[0] - p1[0])
    C = (p1[0]*p2[1] - p2[0]*p1[1])
    return A, B, -C

def intersection(L1, L2):
    D  = L1[0] * L2[1] - L1[1] * L2[0]
    Dx = L1[2] * L2[1] - L1[1] * L2[2]
    Dy = L1[0] * L2[2] - L1[2] * L2[0]
    if D != 0:
        x = Dx / D
        y = Dy / D
        return x,y
    else:
        return False

Usage example:

L1 = line([0,1], [2,3])
L2 = line([2,3], [0,4])

R = intersection(L1, L2)
if R:
    print "Intersection detected:", R
else:
    print "No single intersection point detected"

answered Dec 19 '13 at 10:46

rook

5,880
4
39
51

11

This solution reports intersection where the lines COULD intersect given they have eternal lengths. – firelynx Sep 26 '16 at 14:18
6

@firelynx I think you are confusing the term **line** with **line segment**. The OP asks for a line intersection (on purpose or due to not understanding the difference). When checking lines for intersections on has to take into account the fact that lines are infinite that is the rays that start from its midpoint (defined by the given coordinates of the two points that define it) in both directions. In a case of line segment intersection only the part of the line between the given points is checked for intersection and its infinite continuation is ignored. – rbaleksandar Oct 16 '16 at 13:29
2

Btw how about coinciding lines? Using the algorithm above it returns `true` for two coinciding lines which can obviously not return a single point of intersection (since mathematically speaking there are infinite number of intersection points for this case). I think that the algorithms needs to handle this in a separate case since simply intersecting and coinciding lines are two very different cases. – rbaleksandar Nov 08 '16 at 15:19
1

Yes @rbaleksandar, with this method - when `R` is `true` (`D != 0`) we can say only about intersecting lines. All other cases for `R` (when `D == 0`) can mean anything except intersecting (coinciding or parallel) lines. – rook Nov 10 '16 at 16:30
1

sorry for digging up, but I can't grasp how the values for A, B and C are determined as they are in the first method. can anyone elaborate? Thanks! – Applecow Jan 09 '18 at 06:25
1

@Applecow: C is the determinant of the line. Refer to Paul Draper answer (https://stackoverflow.com/a/20677983/501134) – mrdaliri Dec 14 '19 at 03:34
1

This solution is also particularly good in that you can find the intersection between two lines when one of the lines is vertical. Treating the line as y=mx + c did not allow me to do this as m=infinity when the line is vertical. – Ryan Codrai Dec 16 '21 at 12:36

score 28 · Answer 3 · answered Jun 27 '19 at 12:56

Here is a solution using the Shapely library. Shapely is often used for GIS work, but is built to be useful for computational geometry. I changed your inputs from lists to tuples.

Problem

# Given these endpoints
#line 1
A = (X, Y)
B = (X, Y)

#line 2
C = (X, Y)
D = (X, Y)

# Compute this:
point_of_intersection = (X, Y)

Solution

import shapely
from shapely.geometry import LineString, Point

line1 = LineString([A, B])
line2 = LineString([C, D])

int_pt = line1.intersection(line2)
point_of_intersection = int_pt.x, int_pt.y

print(point_of_intersection)

It's important to be aware that this solution only works if the intersection is between the end points defined, as shapely only finds the intersection of line segments, not of the corresponding infinite lines. — jarlemag, Dec 07 '20 at 02:51

Gabriel Eng · Answer 4 · 2018-07-01T23:31:52.773

23

Using formula from: https://en.wikipedia.org/wiki/Line%E2%80%93line_intersection

 def findIntersection(x1,y1,x2,y2,x3,y3,x4,y4):
        px= ( (x1*y2-y1*x2)*(x3-x4)-(x1-x2)*(x3*y4-y3*x4) ) / ( (x1-x2)*(y3-y4)-(y1-y2)*(x3-x4) ) 
        py= ( (x1*y2-y1*x2)*(y3-y4)-(y1-y2)*(x3*y4-y3*x4) ) / ( (x1-x2)*(y3-y4)-(y1-y2)*(x3-x4) )
        return [px, py]

edited Jul 01 '18 at 23:31

answered Jul 01 '18 at 23:20

Gabriel Eng

321
3
3

1

I am using this bit of code with great success. However I am struggling with how to construct a mechanism to tell me if the point is actually intersecting with the finite line segment, and not the imaginary infinite line. So I need to find if the point x,y is anywhere within the space of (x1,y1,x2,y2). Any ideas? – Mars Nov 19 '20 at 15:15
@Mars were u able to find the mechanism to tell if the point is actually intersecting or not? – Osama Naeem Nov 15 '21 at 05:12
@OsamaNaeem Sorry I dont know. Its quite a while ago. I found a solution but I cant remember it. – Mars Nov 16 '21 at 09:35

score 12 · Answer 5 · answered Feb 11 '19 at 11:05

If your lines are multiple points instead, you can use this version.

import numpy as np
import matplotlib.pyplot as plt
"""
Sukhbinder
5 April 2017
Based on:    
"""

def _rect_inter_inner(x1,x2):
    n1=x1.shape[0]-1
    n2=x2.shape[0]-1
    X1=np.c_[x1[:-1],x1[1:]]
    X2=np.c_[x2[:-1],x2[1:]]    
    S1=np.tile(X1.min(axis=1),(n2,1)).T
    S2=np.tile(X2.max(axis=1),(n1,1))
    S3=np.tile(X1.max(axis=1),(n2,1)).T
    S4=np.tile(X2.min(axis=1),(n1,1))
    return S1,S2,S3,S4

def _rectangle_intersection_(x1,y1,x2,y2):
    S1,S2,S3,S4=_rect_inter_inner(x1,x2)
    S5,S6,S7,S8=_rect_inter_inner(y1,y2)

    C1=np.less_equal(S1,S2)
    C2=np.greater_equal(S3,S4)
    C3=np.less_equal(S5,S6)
    C4=np.greater_equal(S7,S8)

    ii,jj=np.nonzero(C1 & C2 & C3 & C4)
    return ii,jj

def intersection(x1,y1,x2,y2):
    """
INTERSECTIONS Intersections of curves.
   Computes the (x,y) locations where two curves intersect.  The curves
   can be broken with NaNs or have vertical segments.
usage:
x,y=intersection(x1,y1,x2,y2)
    Example:
    a, b = 1, 2
    phi = np.linspace(3, 10, 100)
    x1 = a*phi - b*np.sin(phi)
    y1 = a - b*np.cos(phi)
    x2=phi    
    y2=np.sin(phi)+2
    x,y=intersection(x1,y1,x2,y2)
    plt.plot(x1,y1,c='r')
    plt.plot(x2,y2,c='g')
    plt.plot(x,y,'*k')
    plt.show()
    """
    ii,jj=_rectangle_intersection_(x1,y1,x2,y2)
    n=len(ii)

    dxy1=np.diff(np.c_[x1,y1],axis=0)
    dxy2=np.diff(np.c_[x2,y2],axis=0)

    T=np.zeros((4,n))
    AA=np.zeros((4,4,n))
    AA[0:2,2,:]=-1
    AA[2:4,3,:]=-1
    AA[0::2,0,:]=dxy1[ii,:].T
    AA[1::2,1,:]=dxy2[jj,:].T

    BB=np.zeros((4,n))
    BB[0,:]=-x1[ii].ravel()
    BB[1,:]=-x2[jj].ravel()
    BB[2,:]=-y1[ii].ravel()
    BB[3,:]=-y2[jj].ravel()

    for i in range(n):
        try:
            T[:,i]=np.linalg.solve(AA[:,:,i],BB[:,i])
        except:
            T[:,i]=np.NaN


    in_range= (T[0,:] >=0) & (T[1,:] >=0) & (T[0,:] <=1) & (T[1,:] <=1)

    xy0=T[2:,in_range]
    xy0=xy0.T
    return xy0[:,0],xy0[:,1]


if __name__ == '__main__':

    # a piece of a prolate cycloid, and am going to find
    a, b = 1, 2
    phi = np.linspace(3, 10, 100)
    x1 = a*phi - b*np.sin(phi)
    y1 = a - b*np.cos(phi)

    x2=phi
    y2=np.sin(phi)+2
    x,y=intersection(x1,y1,x2,y2)
    plt.plot(x1,y1,c='r')
    plt.plot(x2,y2,c='g')
    plt.plot(x,y,'*k')
    plt.show()

it is obligatory to have `list` or `nd.array`? – Mir.Emad Jul 08 '20 at 08:18 — Mir.Emad, Jul 08 '20 at 08:18

score 7 · Answer 6 · answered Sep 18 '17 at 21:50

I didn't find an intuitive explanation on the web, so now that I worked it out, here's my solution. This is for infinite lines (what I needed), not segments.

Some terms you might remember:

A line is defined as y = mx + b OR y = slope * x + y-intercept

Slope = rise over run = dy / dx = height / distance

Y-intercept is where the line crosses the Y axis, where X = 0

Given those definitions, here are some functions:

def slope(P1, P2):
    # dy/dx
    # (y2 - y1) / (x2 - x1)
    return(P2[1] - P1[1]) / (P2[0] - P1[0])

def y_intercept(P1, slope):
    # y = mx + b
    # b = y - mx
    # b = P1[1] - slope * P1[0]
    return P1[1] - slope * P1[0]

def line_intersect(m1, b1, m2, b2):
    if m1 == m2:
        print ("These lines are parallel!!!")
        return None
    # y = mx + b
    # Set both lines equal to find the intersection point in the x direction
    # m1 * x + b1 = m2 * x + b2
    # m1 * x - m2 * x = b2 - b1
    # x * (m1 - m2) = b2 - b1
    # x = (b2 - b1) / (m1 - m2)
    x = (b2 - b1) / (m1 - m2)
    # Now solve for y -- use either line, because they are equal here
    # y = mx + b
    y = m1 * x + b1
    return x,y

Here's a simple test between two (infinite) lines:

A1 = [1,1]
A2 = [3,3]
B1 = [1,3]
B2 = [3,1]
slope_A = slope(A1, A2)
slope_B = slope(B1, B2)
y_int_A = y_intercept(A1, slope_A)
y_int_B = y_intercept(B1, slope_B)
print(line_intersect(slope_A, y_int_A, slope_B, y_int_B))

Output:

(2.0, 2.0)

You may want to try this with these points: A1 = [1,1] A2 = [1,3] B1 = [1,3] B2 = [3,1] — Charlie Burns, Nov 21 '17 at 22:19
Anything that represents a line with y = ax + b will crash with vertical lines — Mehdi, Feb 26 '19 at 16:53

score 6 · Answer 7 · answered Dec 07 '20 at 02:48

The most concise solution I have found uses Sympy: https://www.geeksforgeeks.org/python-sympy-line-intersection-method/

# import sympy and Point, Line 
from sympy import Point, Line 
  
p1, p2, p3 = Point(0, 0), Point(1, 1), Point(7, 7) 
l1 = Line(p1, p2) 
  
# using intersection() method 
showIntersection = l1.intersection(p3) 
  
print(showIntersection)

score 3 · Answer 8 · answered May 28 '22 at 15:03

With the scikit-spatial library you can easily do it in the following way:

import matplotlib.pyplot as plt

from skspatial.objects import Line

# Define the two lines.
line_1 = Line.from_points([3, -2], [5, 4])
line_2 = Line.from_points([-1, 0], [3, 2])

# Compute the intersection point
intersection_point = line_1.intersect_line(line_2)

# Plot
_, ax = plt.subplots()
line_1.plot_2d(ax, t_1=-2, t_2=3, c="k")
line_2.plot_2d(ax, t_1=-2, t_2=3, c="k")
intersection_point.plot_2d(ax, c="r", s=100)
grid = ax.grid()

Bob · Answer 9 · 2022-06-04T03:46:34.863

2

there is already an answer that uses formula from Wikipedia but that doesn't have any check point to check if line segments actually intersect so here you go

def line_intersection(a, b, c, d):
    t = ((a[0] - c[0]) * (c[1] - d[1]) - (a[1] - c[1]) * (c[0] - d[0])) / ((a[0] - b[0]) * (c[1] - d[1]) - (a[1] - b[1]) * (c[0] - d[0]))
    u = ((a[0] - c[0]) * (a[1] - b[1]) - (a[1] - c[1]) * (a[0] - b[0])) / ((a[0] - b[0]) * (c[1] - d[1]) - (a[1] - b[1]) * (c[0] - d[0]))

    # check if line actually intersect
    if (0 <= t and t <= 1 and 0 <= u and u <= 1):
        return [a[0] + t * (b[0] - a[0]), a[1] + t * (b[1] - a[1])]
    else: 
        return False
    
#usage
print(line_intersection([0,0], [10, 10], [0, 10], [10,0]))

#result [5.0, 5.0]

edited Jun 04 '22 at 03:46

answered Jun 02 '22 at 09:52

Bob

21
2

If you inspect the more readable and accepted answer of this question you might recognize, that it checks if the lines intersect by calculating the determinant of the x and y diffs. – MaKaNu Jun 02 '22 at 11:50
i was talking about the one with Wikipedia formula which don't have check point @MaKaNu – Bob Jun 02 '22 at 12:31
In this case you should add a link to the answer, you want to improve. You can do this using the share button from the answer. – MaKaNu Jun 02 '22 at 12:58
i was talking about https://stackoverflow.com/a/51127674/19165716 @MaKaNu – Bob Jun 03 '22 at 09:01
1

Yes I understand this already after your last comment. But here are a few answers. instead putting the link into another comment you should edit your answer or even better provide an Edit (if possible to the original answer.) – MaKaNu Jun 03 '22 at 12:57
this worked perfectly i prefer this solution then the top one – مهند عبد الجليل Jan 29 '23 at 16:51

score 0 · Answer 10 · answered May 08 '20 at 03:05

img And You can use this kode

class Nokta:
def __init__(self,x,y):
    self.x=x
    self.y=y             
class Dogru:
def __init__(self,a,b):
    self.a=a
    self.b=b        

def Kesisim(self,Dogru_b):
    x1= self.a.x
    x2=self.b.x
    x3=Dogru_b.a.x
    x4=Dogru_b.b.x
    y1= self.a.y
    y2=self.b.y
    y3=Dogru_b.a.y
    y4=Dogru_b.b.y                          
    #Notlardaki denklemleri kullandım
    pay1=((x4 - x3) * (y1 - y3) - (y4 - y3) * (x1 - x3))      
    pay2=((x2-x1) * (y1 - y3) - (y2 - y1) * (x1 - x3))
    payda=((y4 - y3) *(x2-x1)-(x4 - x3)*(y2 - y1))        

    if pay1==0 and pay2==0 and payda==0:
        print("DOĞRULAR BİRBİRİNE ÇAKIŞIKTIR")

    elif payda==0:               
        print("DOĞRULAR BİRBİRNE PARALELDİR")        
    else:                               
        ua=pay1/payda if payda else 0                   
        ub=pay2/payda  if payda else 0  
        #x ve y buldum 
        x=x1+ua*(x2-x1) 
        y=y1+ua*(y2-y1)
        print("DOĞRULAR {},{} NOKTASINDA KESİŞTİ".format(x,y))

How do I compute the intersection point of two lines?

10 Answers10

Problem

Solution

Linked

Related