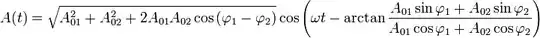Say I have a simple array, with a corresponding probability distribution.
library(stats)
data <- c(0,0.08,0.15,0.28,0.90)
pdf_of_data <- density(data, from= 0, to=1, bw=0.1)
Is there a way I could generate another set of data using the same distribution. As the operation is probabilistic, it need not exactly match the initial distribution anymore, but will be just generated from it.
I did have success finding a simple solution on my own. Thanks!