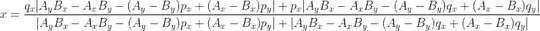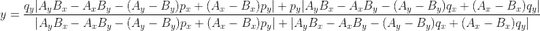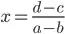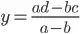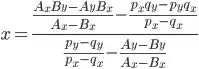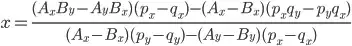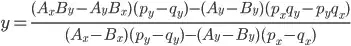The following is C++ code taken from CP3, which calculates the point of intersection between the line that passes through a and b, and the line segment defined by p and q, assuming the intersection exists. Can someone explain what it is doing and why it works (geometrically)?
// line segment p-q intersect with line A-B.
point lineIntersectSeg(point p, point q, point A, point B) {
double a = B.y - A.y;
double b = A.x - B.x;
double c = B.x * A.y - A.x * B.y;
double u = fabs(a * p.x + b * p.y + c);
double v = fabs(a * q.x + b * q.y + c);
return point((p.x * v + q.x * u) / (u+v), (p.y * v + q.y * u) / (u+v));
}
Note that this solution seems to be different to that explained here or in the Wikipedia page since this solution makes use of the absolute value function.
I've expanded the expressions that result for the point of intersection (x, y):