Plot a plane based on a normal vector and a point in Matlab or matplotlib

Question

How would one go plotting a plane in matlab or matplotlib from a normal vector and a point?

Answer 1

For all the copy/pasters out there, here is similar code for Python using matplotlib:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

point  = np.array([1, 2, 3])
normal = np.array([1, 1, 2])

# a plane is a*x+b*y+c*z+d=0
# [a,b,c] is the normal. Thus, we have to calculate
# d and we're set
d = -point.dot(normal)

# create x,y
xx, yy = np.meshgrid(range(10), range(10))

# calculate corresponding z
z = (-normal[0] * xx - normal[1] * yy - d) * 1. /normal[2]

# plot the surface
plt3d = plt.figure().gca(projection='3d')
plt3d.plot_surface(xx, yy, z)
plt.show()

Answer 2

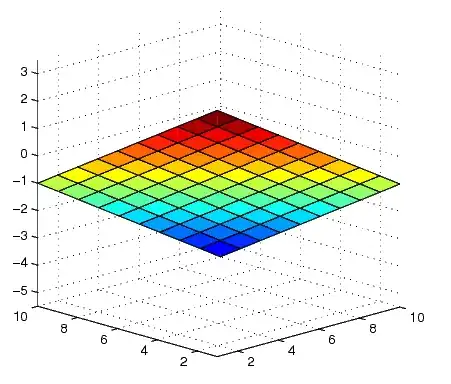
For Matlab:

point = [1,2,3];
normal = [1,1,2];

%# a plane is a*x+b*y+c*z+d=0
%# [a,b,c] is the normal. Thus, we have to calculate
%# d and we're set
d = -point*normal'; %'# dot product for less typing

%# create x,y
[xx,yy]=ndgrid(1:10,1:10);

%# calculate corresponding z
z = (-normal(1)*xx - normal(2)*yy - d)/normal(3);

%# plot the surface
figure
surf(xx,yy,z)

Note: this solution only works as long as normal(3) is not 0. If the plane is parallel to the z-axis, you can rotate the dimensions to keep the same approach:

z = (-normal(3)*xx - normal(1)*yy - d)/normal(2); %% assuming normal(3)==0 and normal(2)~=0

%% plot the surface
figure
surf(xx,yy,z)

%% label the axis to avoid confusion
xlabel('z')
ylabel('x')
zlabel('y')

Answer 3

For copy-pasters wanting a gradient on the surface:

from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import numpy as np
import matplotlib.pyplot as plt

point = np.array([1, 2, 3])
normal = np.array([1, 1, 2])

# a plane is a*x+b*y+c*z+d=0
# [a,b,c] is the normal. Thus, we have to calculate
# d and we're set
d = -point.dot(normal)

# create x,y
xx, yy = np.meshgrid(range(10), range(10))

# calculate corresponding z
z = (-normal[0] * xx - normal[1] * yy - d) * 1. / normal[2]

# plot the surface
plt3d = plt.figure().gca(projection='3d')

Gx, Gy = np.gradient(xx * yy)  # gradients with respect to x and y
G = (Gx ** 2 + Gy ** 2) ** .5  # gradient magnitude
N = G / G.max()  # normalize 0..1

plt3d.plot_surface(xx, yy, z, rstride=1, cstride=1,
                   facecolors=cm.jet(N),
                   linewidth=0, antialiased=False, shade=False
)
plt.show()

Answer 4

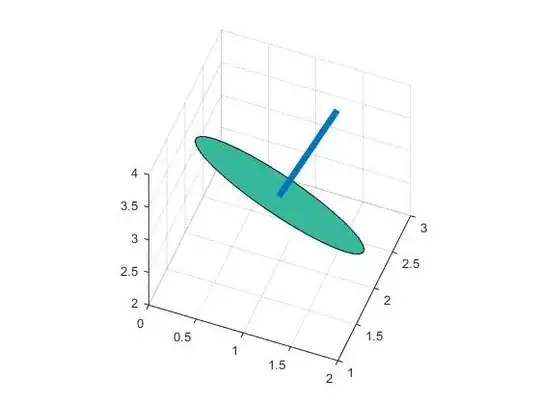
The above answers are good enough. One thing to mention is, they are using the same method that calculate the z value for given (x,y). The draw back comes that they meshgrid the plane and the plane in space may vary (only keeping its projection the same). For example, you cannot get a square in 3D space (but a distorted one).

To avoid this, there is a different way by using the rotation. If you first generate data in x-y plane (can be any shape), then rotate it by equal amount ([0 0 1] to your vector) , then you will get what you want. Simply run below code for your reference.

point = [1,2,3];
normal = [1,2,2];
t=(0:10:360)';
circle0=[cosd(t) sind(t) zeros(length(t),1)];
r=vrrotvec2mat(vrrotvec([0 0 1],normal));
circle=circle0*r'+repmat(point,length(circle0),1);
patch(circle(:,1),circle(:,2),circle(:,3),.5);
axis square; grid on;
%add line
line=[point;point+normr(normal)]
hold on;plot3(line(:,1),line(:,2),line(:,3),'LineWidth',5)

It get a circle in 3D:

Answer 5

A cleaner Python example that also works for tricky $z,y,z$ situations,

from mpl_toolkits.mplot3d import axes3d
from matplotlib.patches import Circle, PathPatch
import matplotlib.pyplot as plt
from matplotlib.transforms import Affine2D
from mpl_toolkits.mplot3d import art3d
import numpy as np

def plot_vector(fig, orig, v, color='blue'):
   ax = fig.gca(projection='3d')
   orig = np.array(orig); v=np.array(v)
   ax.quiver(orig[0], orig[1], orig[2], v[0], v[1], v[2],color=color)
   ax.set_xlim(0,10);ax.set_ylim(0,10);ax.set_zlim(0,10)
   ax = fig.gca(projection='3d')  
   return fig

def rotation_matrix(d):
    sin_angle = np.linalg.norm(d)
    if sin_angle == 0:return np.identity(3)
    d /= sin_angle
    eye = np.eye(3)
    ddt = np.outer(d, d)
    skew = np.array([[    0,  d[2],  -d[1]],
                  [-d[2],     0,  d[0]],
                  [d[1], -d[0],    0]], dtype=np.float64)

    M = ddt + np.sqrt(1 - sin_angle**2) * (eye - ddt) + sin_angle * skew
    return M

def pathpatch_2d_to_3d(pathpatch, z, normal):
    if type(normal) is str: #Translate strings to normal vectors
        index = "xyz".index(normal)
        normal = np.roll((1.0,0,0), index)

    normal /= np.linalg.norm(normal) #Make sure the vector is normalised
    path = pathpatch.get_path() #Get the path and the associated transform
    trans = pathpatch.get_patch_transform()

    path = trans.transform_path(path) #Apply the transform

    pathpatch.__class__ = art3d.PathPatch3D #Change the class
    pathpatch._code3d = path.codes #Copy the codes
    pathpatch._facecolor3d = pathpatch.get_facecolor #Get the face color    

    verts = path.vertices #Get the vertices in 2D

    d = np.cross(normal, (0, 0, 1)) #Obtain the rotation vector    
    M = rotation_matrix(d) #Get the rotation matrix

    pathpatch._segment3d = np.array([np.dot(M, (x, y, 0)) + (0, 0, z) for x, y in verts])

def pathpatch_translate(pathpatch, delta):
    pathpatch._segment3d += delta

def plot_plane(ax, point, normal, size=10, color='y'):    
    p = Circle((0, 0), size, facecolor = color, alpha = .2)
    ax.add_patch(p)
    pathpatch_2d_to_3d(p, z=0, normal=normal)
    pathpatch_translate(p, (point[0], point[1], point[2]))


o = np.array([5,5,5])
v = np.array([3,3,3])
n = [0.5, 0.5, 0.5]

from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')  
plot_plane(ax, o, n, size=3)    
ax.set_xlim(0,10);ax.set_ylim(0,10);ax.set_zlim(0,10)
plt.show()