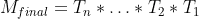The perspective transformation matrix cannot be decomposed into only scale, translate rotate and shear operations. Those operations are all affine, while the perspective transformation is projective (which is not affine; in particular, the perspective will not preserve parallelity of lines).
The "target volume" is an axis-aligned cube in normalized device space. In standard OpenGL, this is going from -1 to 1 in all dimensions (Direct3D, and also Vulkan, use a slightly different convention: [-1,1] for x and y, but [0,1] for z. This means the third row of the matrix will look a bit different, but the concepts are the same).
The projection matrix is constructed such that the pyramid frustum is transformed into that normalized volume. OpenGL also used the convention that in eye space, the camera is oriented towards -z. To create the perspective effect, you simply have to project each point onte a plane, by intersecting the ray conneting the projection center and the point in question with the actual viewing plane.
The above perspective matrix assumes that the image plane is parallel to the xy plane (if you want a different one, you could apply some affine rotation). In OpenGL eye space, the projection center is always at the origin. When you do the math, you will see that the perspective boils down to a simple instance of the intercept theorem. If you want to project all points to a plane which is 1 unit in front of the center ("camera"), you end up with dividing x and y by -z.
This could be written in matrix form as
( 1 0 0 0 )
( 0 1 0 0 )
( 0 0 1 0 )
( 0 0 -1 0 )
It works by setting w_clip = -z_eye, so when the division by clip space w is carried out, we get:
x_ndc = x_clip / w_clip = - x_eye / z_eye
y_ndc = y_clip / w_clip = - y_eye / z_eye
Note that this also applied to z:
z_ndc = z_clip / w_clip = - z_eye / z_eye = 1
Such a matrix is typically not used for rendering, because the depth information is lost - all points are actually porjected onto a single plane. Usually, we want to preserve depth (maybe in some non-linearily deviated way).
To do this, we can tweak the formula for z (third row). Since we do not want any dependency of z on x and y, there is only the last element we can tweak. By using a row of the form
(0 0 A B), we get the following equation:
z_ndc = - A * z_eye / z_eye - B / z_eye = -A - B / z_eye
which is just a hyperbolically transformed variant of the eye space z value - depth is still preserved - and the matrix becomes invertible. We just have to calculate A and B.
Let us call the function z_ndc(z_eye) = -A - B / z_eye just Z(z_eye).
Since the viewing volume is bounded by z_ndc = -1 (front plane) and z_ndc = 1, and the distances of the near and far plane in eye space are given as parameters, we have to map the near plane z_eye=-n to -1, and the far plane z_eye=-f to 1. To chose A and B, we have to solve a system of 2 (non-linear) equations:
Z(-n) = -1
Z(-f) = 1
This will result in exactly the two coefficients you find in the third row of your matrix.
For x and y, we want to control two things: the field of view angle, and the asymetry of the frustum (which is similiar to the "lens shift" known from projectors). The field of view is defined by the x and y range on the image plane which is mapped to [-1,1] in NDC. So you can imagine just an axis-aligned rectangle on an arbitrary plane parallel to image plane. This rectangle describes the part of the scene which is mapped to the visible viewport, at that chosen distance from the camera. Changing the field of view just means scaling that rectangle in x and y.
And conceptually, the lens shift is just a translation, so you might think it should be put in the last column. However, since the division by w=-z will be carried out after the matrix multiplication, we have to multiply that translation by -z first. This means that the translational part is now in the third column, and we have a matrix of the form
( C 0 D 0 )
( 0 E F 0 )
( 0 0 A B )
( 0 0 -1 0 )
For x, this gives:
x_clip = (x_eye * C + D * z_eye ) / (-z_eye) = -x_eye / z_eye - D
Now we just have to find the correct coefficients C and D which will map x_eye=l to x_ndc=-1 and x_eye=r to x_ndc=1. Note that the classical GL frustum function interprets the values of l and r here as distances on the near plane, so we have to calculate all this for z_eye=-n. Solving that new system of 2 equations, you will lead to those coefficients you see in the frustum matrix.