I want to do a simple column (Nx1) times row (1xM) multiplication, resulting in (NxM) matrix. Code where I create a row by sequence, and column by transposing a similar sequence
row1 <- seq(1:6)
col1 <- t(seq(1:6))
col1 * row1
Output which indicates that R thinks matrices more like columns
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1 4 9 16 25 36
Expected output: NxM matrix.
OS: Debian 8.5
Linux kernel: 4.6 backports
Hardware: Asus Zenbook UX303UA
In this case using outer would be a more natural choice
outer(1:6, 1:6)
In general for two numerical vectors x and y, the matrix rank-1 operation can be computed as
outer(x, y)
If you want to resort to real matrix multiplication routines, use tcrossprod:
tcrossprod(x, y)
If either of your x and y is a matrix with dimension, use as.numeric to cast it as a vector first.
It is not recommended to use general matrix multiplication operation "%*%" for this. But if you want, make sure you get comformable dimension: x is a one-column matrix and y is a one-row matrix, so x %*% y.
Can you say anything about efficiency?
Matrix rank-1 operation is known to be memory-bound. So make sure we use gc() for garbage collection to tell R to release memory from heap after every replicate (otherwise your system will stall):
x <- runif(500)
y <- runif(500)
xx <- matrix(x, ncol = 1)
yy <- matrix(y, nrow = 1)
system.time(replicate(200, {outer(x,y); gc();}))
# user system elapsed
# 4.484 0.324 4.837
system.time(replicate(200, {tcrossprod(x,y); gc();}))
# user system elapsed
# 4.320 0.324 4.653
system.time(replicate(200, {xx %*% yy; gc();}))
# user system elapsed
# 4.372 0.324 4.708
In terms of performance, they are all very alike.
Follow-up
When I came back I saw another answer with a different benchmark. Well, the thing is, it depends on the problem size. If you just try a small example you can not eliminate function interpretation / calling overhead for all three functions. If you do
x <- y <- runif(500)
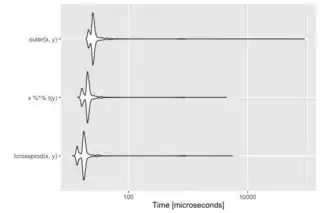
microbenchmark(tcrossprod(x,y), x %*% t(y), outer(x,y), times = 200)
you will see roughly identical performance again.
#Unit: milliseconds
# expr min lq mean median uq max neval cld
# tcrossprod(x, y) 2.09644 2.42466 3.402483 2.60424 3.94238 35.52176 200 a
# x %*% t(y) 2.22520 2.55678 3.707261 2.66722 4.05046 37.11660 200 a
# outer(x, y) 2.08496 2.55424 3.695660 2.69512 4.08938 35.41044 200 a
Here's a comparison of the execution speed for the three methods when the vectors being used are of length 100. The fastest is tcrossprod, with x%*%t(y) taking 17% longer and outer(x,y) taking 45% longer (in median time).
In the table, neval is the number of times the function was evaluated to get the benchmark scores.
> x <- runif(100,0,100)
> y <- runif(100,0,100)
> microbenchmark(tcrossprod(x,y), x%*%t(y), outer(x,y), times=5000)
Unit: microseconds
expr min lq mean median uq max neval
tcrossprod(x, y) 11.404 16.6140 50.42392 17.7300 18.7555 5590.103 5000
x %*% t(y) 13.878 19.4315 48.80170 20.5405 21.7310 4459.517 5000
outer(x, y) 19.238 24.0810 72.05250 25.3595 26.8920 89861.855 5000
To get the the following graph, have
library("ggplot2")
bench <- microbenchmark(tcrossprod(x,y), x%*%t(y), outer(x,y), times=5000)
autplot(bench)
Edit: The performance depends on the size of x and y, and of course the machine running the code. I originally did the benchmark with vectors of length 100 because that's what Masi asked about. However, it appears the three methods have very similar performance for larger vectors. For vectors of length 1000, the median times of the three methods are within 5% of each other on my machine.
> x <- runif(1000)
> y <- runif(1000)
> microbenchmark(tcrossprod(x,y),x%*%t(y),outer(x,y),times=2000)
Unit: milliseconds
expr min lq mean median uq max neval
tcrossprod(x, y) 1.870282 2.030541 4.721175 2.916133 4.482346 75.77459 2000
x %*% t(y) 1.861947 2.067908 4.921061 3.067670 4.527197 105.60500 2000
outer(x, y) 1.886348 2.078958 5.114886 3.033927 4.556067 93.93450 2000
An easy way to look at this is to transform your vectors to a matrix
row1.mat = matrix(row1)
col1.mat = matrix(col1)
and then use dim to see the dimension of the matrices:
dim(row1.mat)
dim(col1.mat)
If you want the product to work for this you need a 6*1 matrix, multiplied by a 1*6 matrix. so you need to transpose the col1.mat using t(col1.mat).
And as you might know the matrix product is %*%
row1.mat %*% t(col1.mat)
Comparison of this method to others
library("microbenchmark")
x <- runif(1000)
y <- runif(1000)
xx = matrix(x)
yy = matrix(y)
microbenchmark(tcrossprod(x,y),x%*%t(y),outer(x,y), xx %*% t(yy), times=2000)
Unit: milliseconds
expr min lq mean median uq max neval
tcrossprod(x, y) 2.829099 3.243785 6.015880 4.801640 5.040636 77.87932 2000
x %*% t(y) 2.847175 3.251414 5.942841 4.810261 5.049474 86.53374 2000
outer(x, y) 2.886059 3.277811 5.983455 4.788054 5.074997 96.12442 2000
xx %*% t(yy) 2.868185 3.255833 6.126183 4.699884 5.056234 87.80024 2000
