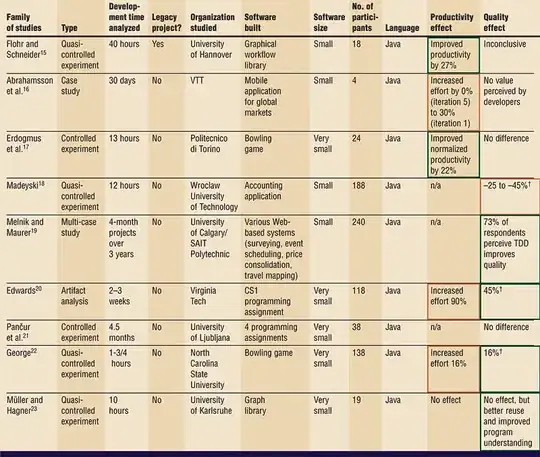
Alright so I decided to make a visualization of this in pygame.
It turned out to be a lot more difficult than I expected.
The idea as in other suggestions is to use Max Flow. The bottleneck in the flow from source to sink is where the flow is most dense. If we cut the graph in half at this dense bottle neck, (i.e. at the min-cut) then we have the minimum number of circles.
It so happens the maxflow = min-cut.
here are the steps I took:
Create pygame world were I can randomly generate circles
Make function to work out all collisions between circles:
This involved sorting the circles by x coordinate. Now to find all collisions of Circle[0] I keep moving along the array testing for collisions until I find a circle who's x value is more than 2*radius greater than circle[0]'s x value, then I can pop circle[0] and repeat the process..
- Create source and sink nodes, work out which circles they need to connect to.
Steps 4-5 are carried out in the "findflow() function"
Create basic undirected networkX graph representing circles with nodes. Connecting nodes only if their corresponding circles collide.
And this is where it starts getting hard.. I create a new directed graph from my undirected graph. Because I needed to work out flow through circles (i.e. nodes) not edges, I need to split each node into two nodes with an edge between.
Lets say I have node X connected to node Y (Y<->X) (in the original graph).
I change X to Xa and Xb so that Xa connects to Xb (Xa->Xb)
Also Y changes to (Ya->Yb).
I also need to add (Yb->Xa) and (Xb->Ya) to represent the original connection between X and Y.
All edges in the undirected graph are given capacity=1 (e.g. you can only cross a circle once)
- I now apply networkx.ford_fulkerson() algorithm on my new directed graph. This finds me the flowValue and the flowGraph.
the flowValue is an integer. It is the min-cut (or max flow from source to sink). This is the answer we have been looking for. It represents the minimum number of circles we are required to remove.
Bonus Assignment:
I thought.. why stop here, having the number of circles to remove is nice, but I want to know the exact circles I need to remove. To do this I need to find out where the min-cut actually occurs on the flowGraph. I managed to figure out how to do this, however my implementation has a bug somewhere, so it sometimes picks the cut slightly wrong and so gets the wrong circles.
To find the min-cut we will use the flowGraph produced in step6. The idea is that the bottleneck of this graph will be the min-cut. if we try flow from source to sink, we will get stuck at the bottle neck as all edges around the bottleneck will be at maximum capacity. So we simply use DFS (Depth first search) to flow down as far as we can. The DFS is only allowed to move along edges that aren't at maximum capacity in the flow graph. (e.g. their flow is 0 not 1). Using DFS from the source I kept note of all nodes I could see storing them in self.seen. Now after DFS, for all the nodes in seen, i check if the node has a maximum capacity edge to a node that wasn't seen in DFS. All such nodes are on the min-cut.
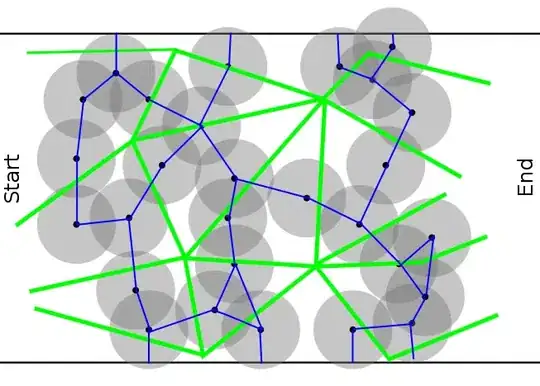
Here is a picture of one of the simulations I ran:

and with the circles removed, I filled it with paint (you may have to zoom in a bit to see that there is indeed a gap between the circles):
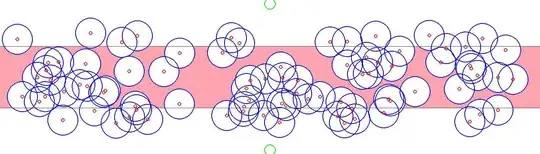
Learnings:
Speed is ok even in python, runs for 1000 circles ok.
It was harder than I thought, and I still have a bug in trying to use the DFS to find the original circles. (If anyone can help find the bug that would be great).
The code was elegant at first, although I kept adding hacks to change the visualization etc.
working code (apart from slight occasional bug in DFS):
__author__ = 'Robert'
import pygame
import networkx
class CirclesThing():
def __init__(self,width,height,number_of_circles):
self.removecircles = False #display removable circles as green.
self.width = width
self.height = height
self.number_of_circles = number_of_circles
self.radius = 40
from random import randint
self.circles = sorted(set((randint(self.radius,width-self.radius),randint(2*self.radius,height-2*self.radius)) for i in range(self.number_of_circles)))
self.sink = (self.width/2, self.height-10)
self.source = (self.width/2, 10)
self.flowValue,self.flowGraph = self.find_flow()
self.seen = set()
self.seen.add(self.source)
self.dfs(self.flowGraph,self.source)
self.removable_circles = set()
for node1 in self.flowGraph:
if node1 not in self.seen or node1==self.source:
continue
for node2 in self.flowGraph[node1]:
if self.flowGraph[node1][node2]==1:
if node2 not in self.seen:
self.removable_circles.add(node1[0])
def find_flow(self):
"finds the max flow from source to sink and returns the amount, along with the flow graph"
G = networkx.Graph()
for node1,node2 in self.get_connections_to_source_sink()+self.intersect_circles():
G.add_edge(node1,node2,capacity=1)
G2 = networkx.DiGraph()
for node in G:
if node not in (self.source,self.sink):
G2.add_edge((node,'a'),(node,'b'),capacity=1) #each node is split into two new nodes. We add the edge between the two new nodes flowing from a to b.
for edge in G.edges_iter():
if self.source in edge or self.sink in edge:
continue #add these edges later
node1,node2 = edge
G2.add_edge((node1,'b'),(node2,'a'),capacity=1) #if we flow through a circle (from node1a to node1b) we need to be able to flow from node1b to all node1's children
G2.add_edge((node2,'b'),(node1,'a'),capactiy=1) #similarly for node2..
for node in G[self.source]:
G2.add_edge(self.source,(node,'a'))
for node in G[self.sink]:
G2.add_edge((node,'b'),self.sink)
flowValue, flowGraph = networkx.ford_fulkerson(G2,self.source,self.sink)
return flowValue, flowGraph
def dfs(self,g,v):
"depth first search from source of flowGraph. Don't explore any nodes that are at maximum capacity. (this means we can't explore past the min cut!)"
for node in g[v]:
if node not in self.seen:
self.seen.add(node)
if g[v][node]!=1 or v==self.source:
self.dfs(g,node)
def display(self):
self.draw_circles()
self.draw_circles(circle_radius=5, circle_colour=(255,0,0))
if not self.removecircles:
lines = self.intersect_circles()
self.draw_lines(lines)
self.draw_source_sink()
def draw_circles(self,circle_radius=None,circle_colour=(0,0,255),circles=None):
if circle_radius is None:
circle_radius = self.radius
if circles is None:
circles = self.circles
circle_thickness = 2
for pos in circles:
cc = circle_colour if pos not in self.removable_circles else (100,200,0) #change colour of removable circles
ct = circle_thickness if pos not in self.removable_circles else 4 #thicken removable circles
if pos not in self.removable_circles or not self.removecircles:
pygame.draw.circle(screen, cc, pos, circle_radius, ct)
def intersect_circles(self):
colliding_circles = []
for i in range(len(self.circles)-1):
for j in range(i+1,len(self.circles)):
x1,y1 = self.circles[i]
x2,y2 = self.circles[j]
if x2-x1>2*self.radius+5: #add 5 to make a more obvious gap visually
break #can't collide anymore.
if (x2-x1)**2 + (y2-y1)**2 <= (2*self.radius)**2+5:
colliding_circles.append(((x1,y1),(x2,y2)))
return colliding_circles
def draw_lines(self,lines,line_colour=(255, 0, 0)):
for point_pair in lines:
point1,point2 = point_pair
try:
tot = self.flowGraph[(point1,'b')][(point2,'a')] + self.flowGraph[(point2,'b')][(point1,'a')] #hack, does anything flow between the two circles?
except KeyError:
tot = 0
thickness = 1 if tot==0 else 3
lc = line_colour if tot==0 else (0,90,90)
pygame.draw.line(screen, lc, point1, point2, thickness)
def draw_source_sink(self):
self.draw_circles(circles=(self.sink,self.source),circle_radius=15,circle_colour=(0,255,0))
bottom_line = ((0,self.height-3*self.radius),(self.width,self.height-3*self.radius))
top_line = ((0,3*self.radius),(self.width,3*self.radius))
self.draw_lines([top_line, bottom_line],line_colour=(60,60,60))
if not self.removecircles:
self.draw_lines(self.get_connections_to_source_sink(),line_colour=(0,255,0))
def get_connections_to_source_sink(self):
connections = []
for x,y in self.circles:
if y<4*self.radius:
connections.append((self.source,(x,y)))
elif y>height-4*self.radius:
connections.append((self.sink,(x,y)))
return connections
def get_caption(self):
return "flow %s, circles removes %s" %(self.flowValue,len(self.removable_circles))
time_per_simulation = 5 #5 seconds
width, height = 1400, 600
background_colour = (255,255,255)
screen = pygame.display.set_mode((width, height))
screen.fill(background_colour)
from pygame.locals import USEREVENT
pygame.time.set_timer(USEREVENT+1,time_per_simulation*1000)
simulations = 0
simulations_max = 20
running = True
while running:
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False
if event.type == USEREVENT+1:
if simulations % 2 ==0:
world = CirclesThing(width,height,120) #new world
else:
world.removecircles = True #current world without green circles
screen.fill(background_colour)
world.display()
pygame.display.set_caption(world.get_caption())
pygame.display.flip()
if simulations>=2*simulations_max:
running = False
simulations+=1
if False:
pygame.image.save(screen,'sim%s.bmp'%simulations)