Find a point, a given distance, along a simple cubic bezier curve. (On an iPhone!)

Question

Imagine you have a completely normal four-point bezier curve (two points and two control points) created using curveToPoint:controlPoint1:controlPoint2: in your cocoa application:

How do you find points (and the tangents), along the curve?

---

Later: for a complete, simplified, solution based on Michal's answer below, click to:
Find the tangent of a point on a cubic bezier curve (on an iPhone)

And just copy and paste the code from: https://stackoverflow.com/a/31317254/294884

Answer 1

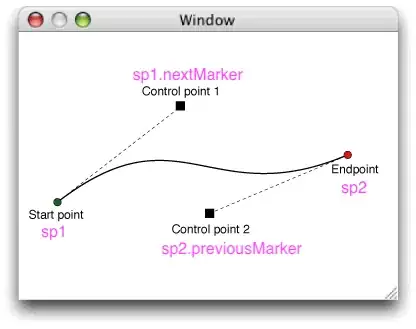
There's some simple math behind calculating the positions, you can read about it in every paper discussing Bézier curves, even on wikipedia. Anyway, I can relate to everybody who's in trouble to actually implement it in code, so I wrote this sample UIView as it's probably the easiest way to get you started.

#import "MBBezierView.h"

CGFloat bezierInterpolation(CGFloat t, CGFloat a, CGFloat b, CGFloat c, CGFloat d) {
    CGFloat t2 = t * t;
    CGFloat t3 = t2 * t;
    return a + (-a * 3 + t * (3 * a - a * t)) * t
    + (3 * b + t * (-6 * b + b * 3 * t)) * t
    + (c * 3 - c * 3 * t) * t2
    + d * t3;
}

@implementation MBBezierView

- (void)drawRect:(CGRect)rect {
    CGPoint p1, p2, p3, p4;
    p1 = CGPointMake(30, rect.size.height * 0.33);
    p2 = CGPointMake(CGRectGetMidX(rect), CGRectGetMinY(rect));
    p3 = CGPointMake(CGRectGetMidX(rect), CGRectGetMaxY(rect));
    p4 = CGPointMake(-30 + CGRectGetMaxX(rect), rect.size.height * 0.66);

    [[UIColor blackColor] set];
    [[UIBezierPath bezierPathWithRect:rect] fill];

    [[UIColor redColor] setStroke];

    UIBezierPath *bezierPath = [[[UIBezierPath alloc] init] autorelease];   
    [bezierPath moveToPoint:p1];
    [bezierPath addCurveToPoint:p4 controlPoint1:p2 controlPoint2:p3];
    [bezierPath stroke];

    [[UIColor brownColor] setStroke];
    for (CGFloat t = 0.0; t <= 1.00001; t += 0.05) {
        CGPoint point = CGPointMake(bezierInterpolation(t, p1.x, p2.x, p3.x, p4.x), bezierInterpolation(t, p1.y, p2.y, p3.y, p4.y));
        UIBezierPath *pointPath = [UIBezierPath bezierPathWithArcCenter:point radius:5 startAngle:0 endAngle:2*M_PI clockwise:YES];
        [pointPath stroke];
    }   
}

@end

This is what I get:

Answer 2

The approximation that t is the distance along the curve that Michal is proposing can be troublesome with some curves and for some purposes. Sadly I've searched without luck for quite a while for an Obj-C implementation of the correct solution.

The solution is, however, described in a rather fantastic way by Mike "Pomax" Kamermans in his amazing Primer on Bezier Curves. It even has all the code, written in processing and in public domain. I'm astonished no one has converted this to Obj-C yet. Very tempted, that I am.

Answer 3

Any Beziér curve can be simply viewed as a polynomial function with vector or complex coefficients. A cubic Beziér curve such as the one in your screenshot, would then be generated by a polynomial function of order 3, and each point on the curve describes the result B(t) of the curve polynomial, evaluated for a particular input value t. If I'm not mistaken, once you know the polynomial used to create the curve, you can simply solve for B(t) = a+bi, where a+bi describes the point on the complex plane you want to find the t value for. Finding roots in polynomials like that is a well-understood problem, and can be solved algebraically for curves of order 2 or lower, and using some method like forward-newton for polynomials of higher degree. If you know the generating polynomial, it should of course also be very simple to find the derivatives. Beziér are usually drawn from "template polynomials" where only the coefficients are changed when a different curve is drawn, so you can probably look it up somewhere in the documentation.

Answer 4

Based on Michal's answer, wrote this in Swift for my project. Maybe will be helpful, just leave it here with explanation on original Fattie's screenshot:

let targetPoint = CGPoint(x: bezierInterpolation(t: distance, p1: sP1.point.x, cp1: sP1.nextMarker.x, cp2: sP2.previousMarker.x, p2: sP2.point.x),
                          y: bezierInterpolation(t: distance, p1: sP1.point.y, cp1: sP1.nextMarker.y, cp2: sP2.previousMarker.y, p2: sP2.point.y))

func bezierInterpolation(t: CGFloat, p1: CGFloat, cp1: CGFloat, cp2: CGFloat, p2: CGFloat) -> CGFloat {
    let t2: CGFloat = t * t;
    let t3: CGFloat = t2 * t;
    return p1 + (-p1 * 3 + t * (3 * p1 - p1 * t)) * t
    + (3 * cp1 + t * (-6 * cp1 + cp1 * 3 * t)) * t
    + (cp2 * 3 - cp2 * 3 * t) * t2
    + p2 * t3;
}