Simple & fast diagonal rectangle slice.
Looking at the other answers I see that they have all a little over complicated the problem. The following is an order of magnitude quicker than the accepted answer and does not require any complicated data structures, iterators, or generate dead memory and unneeded GC hits. It returns the hex cell row and column for any related set of R, H, S or W. The example uses R = 50.
Part of the problem is finding which side of a rectangle a point is if the rectangle is split diagonally. This is a very simple calculation and is done by normalising the position of the point to test.
Slice any rectangle diagonally
Example a rectangle of width w, and height h split from top left to bottom right. To find if a point is left or right. Assume top left of rectangle is at rx,ry
var x = ?;
var y = ?;
x = ((x - rx) % w) / w;
y = ((y - ry) % h) / h;
if (x > y) {
// point is in the upper right triangle
} else if (x < y) {
// point is in lower left triangle
} else {
// point is on the diagonal
}
If you want to change the direction of the diagonal then just invert one of the normals
x = 1 - x; // invert x or y to change the direction the rectangle is split
if (x > y) {
// point is in the upper left triangle
} else if (x < y) {
// point is in lower right triangle
} else {
// point is on the diagonal
}
Split into sub cells and use %
The rest of the problem is just a matter of splitting the grid into (R / 2) by (H / 2) cells width each hex covering 4 columns and 2 rows. Every 1st column out of 3 will have diagonals. with every second of these column having the diagonal flipped. For every 4th, 5th, and 6th column out of 6 have the row shifted down one cell. By using % you can very quickly determine which hex cell you are on. Using the diagonal split method above make the math easy and quick.
And one extra bit. The return argument retPos is optional. if you call the function as follows
var retPos;
mainLoop(){
retPos = getHex(mouse.x, mouse.y, retPos);
}
the code will not incur a GC hit, further improving the speed.
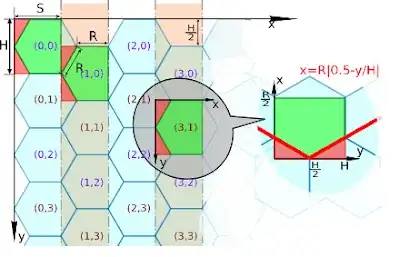
Pixel to Hex coordinates
From Question diagram returns hex cell x,y pos. Please note that this function only works in the range 0 <= x, 0 <= y if you need negative coordinates subtract the min negative pixel x,y coordinate from the input
// the values as set out in the question image
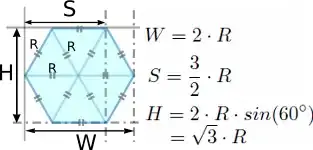
var r = 50;
var w = r * 2;
var h = Math.sqrt(3) * r;
// returns the hex grid x,y position in the object retPos.
// retPos is created if not supplied;
// argument x,y is pixel coordinate (for mouse or what ever you are looking to find)
function getHex (x, y, retPos){
if(retPos === undefined){
retPos = {};
}
var xa, ya, xpos, xx, yy, r2, h2;
r2 = r / 2;
h2 = h / 2;
xx = Math.floor(x / r2);
yy = Math.floor(y / h2);
xpos = Math.floor(xx / 3);
xx %= 6;
if (xx % 3 === 0) { // column with diagonals
xa = (x % r2) / r2; // to find the diagonals
ya = (y % h2) / h2;
if (yy % 2===0) {
ya = 1 - ya;
}
if (xx === 3) {
xa = 1 - xa;
}
if (xa > ya) {
retPos.x = xpos + (xx === 3 ? -1 : 0);
retPos.y = Math.floor(yy / 2);
return retPos;
}
retPos.x = xpos + (xx === 0 ? -1 : 0);
retPos.y = Math.floor((yy + 1) / 2);
return retPos;
}
if (xx < 3) {
retPos.x = xpos + (xx === 3 ? -1 : 0);
retPos.y = Math.floor(yy / 2);
return retPos;
}
retPos.x = xpos + (xx === 0 ? -1 : 0);
retPos.y = Math.floor((yy + 1) / 2);
return retPos;
}
Hex to pixel
And a helper function that draws a cell given the cell coordinates.
// Helper function draws a cell at hex coordinates cellx,celly
// fStyle is fill style
// sStyle is strock style;
// fStyle and sStyle are optional. Fill or stroke will only be made if style given
function drawCell1(cellPos, fStyle, sStyle){
var cell = [1,0, 3,0, 4,1, 3,2, 1,2, 0,1];
var r2 = r / 2;
var h2 = h / 2;
function drawCell(x, y){
var i = 0;
ctx.beginPath();
ctx.moveTo((x + cell[i++]) * r2, (y + cell[i++]) * h2)
while (i < cell.length) {
ctx.lineTo((x + cell[i++]) * r2, (y + cell[i++]) * h2)
}
ctx.closePath();
}
ctx.lineWidth = 2;
var cx = Math.floor(cellPos.x * 3);
var cy = Math.floor(cellPos.y * 2);
if(cellPos.x % 2 === 1){
cy -= 1;
}
drawCell(cx, cy);
if (fStyle !== undefined && fStyle !== null){ // fill hex is fStyle given
ctx.fillStyle = fStyle
ctx.fill();
}
if (sStyle !== undefined ){ // stroke hex is fStyle given
ctx.strokeStyle = sStyle
ctx.stroke();
}
}