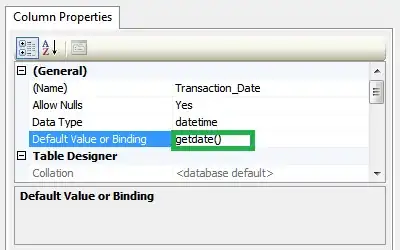
An old unanswered question which I find pretty interesting. Of course, you can always manually plot your arrows and fill the areas which doesn't make sense especially for larger number of points. I am not aware that there is such a Voronoi-feature in gnuplot. This might be especially useful, when coloring a map with datapoints in an irregular grid. I am aware that gnuplot has some interpolation feature (check help dgrid3d).
In the past, I tried a gnuplot implementation of Delaunay-Triangulation, which, however, is pretty slow. Apparently, the Voronoi approach below seems to be much faster.
This procedure seems to run with O(n^2), i.e. for 100, 200, 400 datapoints my old laptop needs approximately 3, 11, and 40 seconds, respectively.
What it does:
- determine for a given point
p0 the perpendicular bisectors to all other points and store them as vectors (x,y,a=angle) in $Vectors.
- furthermore, add the boundaries (
xmin,ymax,ymin,ymax) as vectors as well.
- determine the vector (except the borders) with the smallest distance to point
p0 (which will be in p1).
- calculate all intersections of this vector with all other vectors (except itself and the previous one). Find the closest intersection in counterclockwise direction (which will be in
p2).
- continue until you end up with the first
p1 again.
My explanations and the script are probably not so easy to understand.
Both can certainly be improved. Suggestions are welcome!
For example, maybe the use of arrays might be faster than writing to a datablock.
Comment: There seems to be still a small bug in the script. Sometimes, it can happen that some areas (especially) at the border are not filled correctly.
Script: (requires gnuplot 5.2.0, Sept. 2017, because of indexing of datablocks)
### plot Voronoi-diagram from given set of points
reset session
time0 = time(0.0)
FILE = "SO40883823.dat"
# create some random test data
set table $Data
set samples 100
plot '+' u (sprintf("%g %g %g",x0=rand(0), y0=rand(0), z0=(int(rand(0)*0xffffff)))) w table
# plot FILE u 1:2:3 w table
unset table
set size square
set key noautotitle
xmin = 0 # adjust the borders
xmax = 1
ymin = 0
ymax = 1
set xrange[xmin:xmax]
set yrange[ymin:ymax]
set tics out
set offset 0.01,0.01,0.01,0.01
set angle degrees
j = {0,1}
x(i) = real(word($Data[i],1))
y(i) = real(word($Data[i],2))
z(i) = real(word($Data[i],3))
getDmin(colX,colY,colA,colL) = (L=column(colL), \
column(colA)==column(colA) || column(0)<3 ? dmin!=dmin ? \
(idx1=column(0),x1=column(colX),y1=column(colY),a1=column(colA),dmin=L) : L<dmin ? \
(idx1=column(0),x1=column(colX),y1=column(colY),a1=column(colA),dmin=L) : 0 : NaN)
M(x,y,a) = ((x-x0)*sin(a0) - (y-y0)*cos(a0))/(sin(a)*cos(a0)-sin(a0)*cos(a))
xs(x,y,a) = M(x,y,a)==0 ? NaN : x + cos(a)*M(x,y,a)
ys(x,y,a) = M(x,y,a)==0 ? NaN : y + sin(a)*M(x,y,a)
# orientation of 3 2D-points p0,p1,p2: -1=clockwise, 0=linear, +1=counterclockwise
Orientation(p0,p1,p2) = sgn((real(p1)-real(p0))*(imag(p2)-imag(p0)) - \
(real(p2)-real(p0))*(imag(p1)-imag(p0)))
colX = 1
colY = 2
colA = 3
colL = 4
set print $Outlines
print "" # initialize datablock
set print
do for [i=1:|$Data|] {
set print $Vectors
print sprintf("%g %g %g %g %g", x(i), ymin, 0, y(i)-ymin, 0) # bottom border
print sprintf("%g %g %g %g %g", xmax, y(i), 90, xmax-x(i), 1) # right
print sprintf("%g %g %g %g %g", x(i), ymax, 180, ymax-y(i), 2) # top
print sprintf("%g %g %g %g %g", xmin, y(i), 270, x(i)-xmin, 3) # left
x00 = x(i)
y00 = y(i)
z00 = z(i)
p0 = x00 + j*y00
do for [k=1:|$Data|] {
x0 = (x00 + x(k))/2.
y0 = (y00 + y(k))/2.
dx = x(k)-x00
dy = y(k)-y00
a0 = dx==0 && dy==0 ? NaN : atan2(dy,dx)+90
dL = sqrt(dx**2 + dy**2)
print sprintf("%g %g %g %g %g", x0, y0, a0, dL, k+3)
}
set print
# get vector with minimal distance from p0
dmin = NaN
stats [*:*][*:*] $Vectors u (getDmin(colX,colY,colA,colL)) nooutput # get x1,y1,a1,idx1
p1 = x1 + j*y1
set print $Outlines append
print sprintf("# Outline for point %g: %g,%g", i, x00,y00)
set print
idxC = idx00 = idx1
k = 0
while (idxC!=idx00 || k<2) {
k=k+1
x0 = x1; y0=y1; a0=a1; idx0 = idx1; idx2=idx1;
dmin = p2m = NaN
stats [*:*][*:*] $Vectors u ($0==idx0 || $0==idxC ? NaN : \
sprintf("%g %g %g %g %g", xc=xs($1,$2,$3), \
yc=ys($1,$2,$3), (p2=xc+j*yc, ox=Orientation(p0,p1,p2)), \
(dL = (x0-xc)**2+(y0-yc)**2), \
(ox==1 ? dmin!=dmin ? \
(x1=xc, y1=yc, a1=$3, idx1=$0, p2m=p2, dmin=dL) : dL<dmin ? \
(x1=xc, y1=yc, a1=$3, idx1=$0, p2m=p2, dmin=dL) : dmin : dmin,$0))) nooutput
set print $Outlines append
print sprintf("%g %g %g % 2d",x1, y1, z00, idx0)
set print
p1 = p2m
idx2 = idx1
idxC = idx0
}
set print $Outlines append
print ""; print ""
set print
print sprintf("Point: % 3d",i)
}
plot for [i=0:*] $Outlines u 1:2:3 index i w filledcurves lc rgb var fs solid 0.5, \
$Data u 1:2 w p pt 7 ps 0.5 lc "black"
print sprintf("Elapsed time: %.3f sec", time(0.0)-time0)
### end of script
Result:
OP's data from file as SO40883823.dat with some colors in third column. In order to create this, comment line 10 and uncomment line 11 in the above script. The illustration below has some additional point numbering (not in the script).
0 0 0xff0000
100 0 0x00ff00
0 100 0x0000ff
100 100 0xff00ff
10 20 0xee82ee
25 60 0xffff00
35 80 0xffa544
40 30 0x00ffff
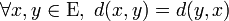
With some random test data generation: 100 points
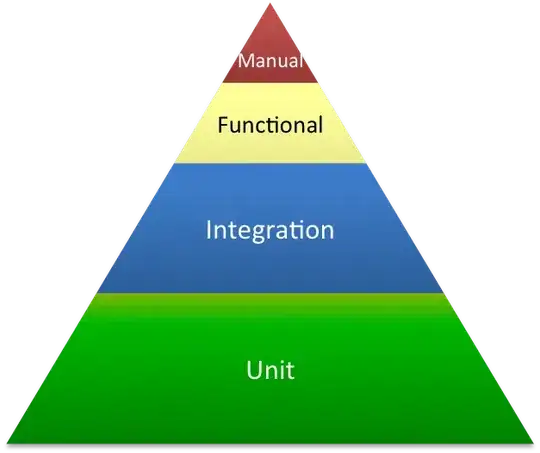
... and 400 points: