What I found so far: a commonly used method, e.g. in finite element simulations, is meshing or triangulation.
The following is an attempt of a gnuplot implementation of the "Delaunay Triangulation" of a set of points. https://en.wikipedia.org/wiki/Delaunay_triangulation
However, I'm aware that gnuplot is not really the tool for such a task.
So, probably, there are better solutions which I am not aware of. I am curious to learn about them.
Delaunay triangulation:
The following code is certainly not the most efficient way to get the triangulation, improvements are welcome
Procedure (short version):
- sort your N data points by increasing x and if identical x then by increasing y
- find the first m>=3 points which are not collinear
- loop points from m to N
3.1) find all hull points whose connections to point m+1 do not intersect with any current hull segment
3.2) connect these hull points to point m+1 and modify the hull accordingly
- loop all inner edges
4.1) find the 2 triangles containing the current edge. These form a quadrangle
4.2) if the quadrangle is convex, check if the diagonal needs to be flipped ("Lawson-flip")
4.3) start over with 4) until no flips are necessary anymore
In order to color the triangles
- split each triangle into 3 quadrangles using the centroid as a 4th point
- color the 3 sub-quadrangles according to the z-value of the respective data point
Comments:
- gnuplot has no native sort capability (especially sorting by >=2 columns), so you have to use
sort (already included on Linux, on Windows you have to install, e.g. CoreUtils from GnuWin.
- Flipping the edges will take some time. I guess, it scales with
O(n^2). So, above 100 datapoints it becomes unpractial, because it will simply take too long. But there seem to be algorithms which should run in O(n log n).
- Improvements are welcome, or maybe even an implementation in gnuplot would be great ;-)
Code:
### Delaunay triangulation (gnuplot implementation attempt, requires gnuplot 5.4)
reset session
# get some test data
Random=0 # set to 0 to read data from existing FILE
if (Random) {
FILE = "tbTriangulationRandom.dat"
set print FILE
do for [i=0:99] {
print sprintf("%g %g %g",x=invnorm(rand(0))*10,y=invnorm(rand(0))*10,x*y)
}
set print
}
else {
FILE = "tbTriangulationTest.dat"
}
# sort data by x increasing values and if x is identical by increasing y values
set table $Data
plot '<sort -n -k 1 -k 2 '.FILE u 1:2:3 w table
unset table
# definition of quite a few variables and functions
colX = 1 # x column
colY = 2 # y column
colZ = 3 # z column
N = |$Data| # number of points
EDGES = '' # list of (inner) edges
HULL = '' # list of hull segments
TRIANGLES = '' # list of triangles
HULLPOINTS = '' # list of hullpoints
array Px[N] # set point array size
array Py[N] # set point array size
array Pz[N] # set point array size
newEdge(p1,p2) = sprintf(" %d %d ",p1,p2)
Edge(n) = sprintf(" %s %s ",word(EDGES,2*n-1),word(EDGES,2*n))
EdgeP(n,p) = int(word(EDGES,2*n-2+p))
changeEdge(n,p1,p2) = (_edge=Edge(n), _pos = strstrt(EDGES,_edge), _pos ? \
EDGES[1:_pos-1].newEdge(p1,p2). \
EDGES[_pos+strlen(_edge):strlen(EDGES)] : EDGES)
TriangleCount(n) = words(TRIANGLES)/3
TriangleN(n) = sprintf(" %s %s %s ", \
word(TRIANGLES,3*n-2),word(TRIANGLES,3*n-1),word(TRIANGLES,3*n))
newTriangle(p1,p2,p3) = p1<p2 && p2<p3 ? sprintf(" %d %d %d ",p1,p2,p3) : \
p1<p3 && p3<p2 ? sprintf(" %d %d %d ",p1,p3,p2) : \
p2<p1 && p1<p3 ? sprintf(" %d %d %d ",p2,p1,p3) : \
p2<p3 && p3<p1 ? sprintf(" %d %d %d ",p2,p3,p1) : \
p3<p1 && p1<p2 ? sprintf(" %d %d %d ",p3,p1,p2) : \
sprintf(" %d %d %d ",p3,p2,p1)
changeTA(n,p1,p2,p3) = (TA=TriangleN(n), _pos = strstrt(TRIANGLES,TA), _pos ? \
TRIANGLES[1:_pos-1].newTriangle(p1,p2,p3). \
TRIANGLES[_pos+strlen(TA):strlen(TRIANGLES)] : TRIANGLES)
TAp(n,p) = int(word(TRIANGLES,3*n-3+p))
TAx(n,p) = Px[TAp(n,p)] # x-coordinate of point p of triangle n
TAy(n,p) = Py[TAp(n,p)] # y-coordinate of point p of triangle n
HullP(n,p) = int(word(HULL,2*n-2+p)) # hull segment point number
HScount(n) = int(words(HULL))/2 # number of hull segments
getHullPoints(n) = (_tmp = '', sum [_i=1:words(HULL)] ((_s=' '.word(HULL,_i).' ', _tmp = \
strstrt(_tmp,_s) ? _tmp : _tmp._s ), 0), _tmp)
removeFromHull(seg) = (seg, _pos = strstrt(HULL,seg), _pos ? \
HULL[1:_pos-1].HULL[_pos+strlen(seg):strlen(HULL)] : HULL)
# orientation of 3 points, either -1=clockwise, 0=collinear, 1=counterclockwise
Orientation(p1,p2,p3) = sgn((Px[p2]-Px[p1])*(Py[p3]-Py[p1]) - (Px[p3]-Px[p1])*(Py[p2]-Py[p1]))
# check for intersection of segment p1-p2 with segment p3-p4, 0=no intersection, 1=intersection
IntersectCheck(p1,p2,p3,p4) = (Orientation(p1,p3,p2)==Orientation(p1,p4,p2)) || \
(Orientation(p3,p1,p4)==Orientation(p3,p2,p4)) ? 0 : 1
Sinus(p1,p2) = (_dx=Px[p2]-Px[p1], _dy=Py[p2]-Py[p1], _dy/sqrt(_dx**2 + _dy**2))
### Macros for later use
# Creating inner edges datablock macro
CreateEdgeDatablock = '\
set print $EDGES; \
do for [i=1:words(EDGES)/2] { \
p1 = int(word(EDGES,2*i-1)); \
p2 = int(word(EDGES,2*i)); \
print sprintf("%g %g %g %g %d %d",Px[p1],Py[p1],Px[p2]-Px[p1],Py[p2]-Py[p1],p1,p2) \
}; \
set print '
# Creating hull datablock macro
CreateHullDatablock = '\
set print $HULL; \
do for [i=1:words(HULL)/2] { \
p1 = int(word(HULL,2*i-1)); \
p2 = int(word(HULL,2*i)); \
print sprintf("%g %g %g %g %d %d",Px[p1],Py[p1],Px[p2]-Px[p1],Py[p2]-Py[p1],p1,p2) \
}; \
set print '
# plotting everything
PlotEverything = '\
plot $EDGES u 1:2:3:4 w vec lw 1.0 lc "red" nohead, \
$HULL u 1:2:3:4 w vec lw 1.5 lc "blue" nohead, \
$Data u 1:2 w p pt 7 ps 0.5 lc "black", \
$Data u 1:2:($0+1) w labels offset 0.5,0.5 '
# put datpoints into arrays
set table $Dummy
plot $Data u (Px[int($0)+1]=column(colX),Py[int($0)+1]=column(colY),Pz[int($0)+1]=column(colZ),'') w table
unset table
# get first m>=3 points which are not all collinear
HULL = HULL.newEdge(1,2) # add first 2 points to hull in any case
do for [p=3:N] {
if (Orientation(p-2,p-1,p)==0) { # orientation==0 if collinear
HULL = HULL.newEdge(p-1,p)
}
else { break } # stop if first >=3 non-collinear points found
}
HPcountInit = words(getHullPoints(0)) # get initial number of hull points
# actual plotting starts from here
set offset 1,1,1,1
set key noautotitle
set palette rgb 33,13,10
set rmargin screen 0.8
plot $Data u 1:2 w p pt 7 ps 0.5 lc "black", \
'' u 1:2:($0+1) w labels offset 0.5,0.5
set label 1 at graph 0.02,0.97 "Adding points... "
# loop all data points
do for [p=HPcountInit+1:N] {
print sprintf("### Adding P%d",p)
HPlist = getHullPoints(0)
HPcount = words(HPlist)
set print $NewConnections # initalize/empty datablock for new connections
print ""
set print
do for [hpt in HPlist] { # loop and check all hull points
hp = int(hpt)
# print sprintf("Check hull point P%d", hp)
c = 0
do for [hs=1:HScount(0)] { # loop all hull segments
hp1 = HullP(hs,1)
hp2 = HullP(hs,2)
# print sprintf("Check %d-%d with %d-%d", hp1, hp2, hp, p)
if (p!=hp1 && p!=hp2 && hp!=hp1 && hp!=hp2) {
c = c || IntersectCheck(hp1,hp2,hp,p)
if (c) { break }
}
}
if (c==0) { # if no intersections with hull
set print $NewConnections append # add new connections to datablock
print sprintf("%g %g", hp, Sinus(p,hp))
set print
}
}
# sort datablock clockwise (a bit cumbersome in gnuplot)
set table $ConnectSorted
plot $NewConnections u 1:2:2 smooth zsort # requires gnuplot 5.4.0
set table $Dummy
plot Connect='' $ConnectSorted u (Connect=Connect.sprintf(" %d",$1),'') w table
unset table
# add new edges
Ccount = int(words(Connect))
do for [i=1:Ccount-1] {
p1 = int(word(Connect,i))
p2 = int(word(Connect,i+1))
TRIANGLES = TRIANGLES.sprintf(" %d %d %d ", p1<p2?p1:p2, p2<p1?p1:p2, p) # numbers in ascending order
if (i==1) { HULL=HULL.newEdge(p1,p) }
if (i>1 && i<Ccount) { EDGES = EDGES.newEdge(p1,p) }
if (i==Ccount-1) {
HULL = HULL.newEdge(p2,p)
}
if (p!=HPcountInit+1) { # remove hull segments, except initial ones
NewEdge = p1<p2 ? sprintf(" %d %d ",p1,p2) : sprintf(" %d %d ",p2,p1)
# print sprintf("Remove %s",NewEdge)
HULL = removeFromHull(NewEdge)
EDGES = EDGES.NewEdge
@CreateEdgeDatablock
@CreateHullDatablock
@PlotEverything
}
}
}
# flip diagonal of a quadrangle if Det(p1,p2,p3,p4) and Orientation(p1,p2,p3) have the same sign
#
m11(p1,p4) = Px[p1]-Px[p4]
m21(p2,p4) = Px[p2]-Px[p4]
m31(p3,p4) = Px[p3]-Px[p4]
m12(p1,p4) = Py[p1]-Py[p4]
m22(p2,p4) = Py[p2]-Py[p4]
m32(p3,p4) = Py[p3]-Py[p4]
m13(p1,p4) = (Px[p1]-Px[p4])**2 + (Py[p1]-Py[p4])**2
m23(p2,p4) = (Px[p2]-Px[p4])**2 + (Py[p2]-Py[p4])**2
m33(p3,p4) = (Px[p3]-Px[p4])**2 + (Py[p3]-Py[p4])**2
Det(p1,p2,p3,p4) = m11(p1,p4)*(m22(p2,p4)*m33(p3,p4) - m32(p3,p4)*m23(p2,p4)) + \
m12(p1,p4)*(m23(p2,p4)*m31(p3,p4) - m33(p3,p4)*m21(p2,p4)) + \
m13(p1,p4)*(m21(p2,p4)*m32(p3,p4) - m31(p3,p4)*m22(p2,p4))
# create triangle data
set print $Triangles
do for [i=1:TriangleCount(0)] {
print sprintf("%g %g",TAx(i,1),TAy(i,1))
print sprintf("%g %g",TAx(i,2),TAy(i,2))
print sprintf("%g %g",TAx(i,3),TAy(i,3))
print sprintf("%g %g",TAx(i,1),TAy(i,1))
print ""
}
unset print
@CreateEdgeDatablock
@CreateHullDatablock
@PlotEverything
set label 1 "Flipping diagonals... "
###
# loop edges and check if need to flip. If on edge was flipped, start over again.
flip = 0
flipCount = 0
flippedAtLeastOnce = 1
while (flippedAtLeastOnce) {
flippedAtLeastOnce=0
do for [e=1:words(EDGES)/2] { # loop all inner edges
# find the 2 triangles with this edge
p1 = EdgeP(e,1)
p2 = EdgeP(e,2)
found = 0
do for [t=1:TriangleCount(0)] { # loop all triangles
tap1 = TAp(t,1)
tap2 = TAp(t,2)
tap3 = TAp(t,3)
p = p1==tap1 ? p2==tap2 ? tap3 : p2==tap3 ? tap2 : 0 : p1==tap2 ? p2==tap3 ? tap1 : 0 : 0
# print sprintf("%d %d %d: %d",tap1,tap2,tap3,p)
if (p!=0) {
if (found==1) {
ta2=t; p4=p;
flip = sgn(Det(p1,p2,p3,p4))==Orientation(p1,p2,p3)
flippedAtLeastOnce = flippedAtLeastOnce || flip
if (flip) {
flipCount = flipCount+1
print sprintf("Flip % 3d: %d-%d with %d-%d",flipCount,p1,p2,p3,p4)
EDGES = changeEdge(e,p3,p4)
TRIANGLES = changeTA(ta1,p1,p3,p4)
TRIANGLES = changeTA(ta2,p2,p3,p4)
@CreateEdgeDatablock
@CreateHullDatablock
@PlotEverything
break # start over again
}
}
if (found==0) { ta1=t; p3=p; found=1}
}
}
}
}
###
# create quadrangles datablock
Center2x(p1,p2) = (Px[p1]+Px[p2])/2. # x-center of 2 points
Center2y(p1,p2) = (Py[p1]+Py[p2])/2. # y-center of 2 points
Center3x(p1,p2,p3) = (Px[p1]+Px[p2]+Px[p3])/3. # x-center between 3 points
Center3y(p1,p2,p3) = (Py[p1]+Py[p2]+Py[p3])/3. # x-center between 3 points
set print $QUADRANGLES
do for [i=1:TriangleCount(0)] {
do for [p=0:2] {
z = Pz[TAp(i,p+1)]
tap1 = TAp(i,p+1)
tap2 = TAp(i,(p+1)%3+1)
tap3 = TAp(i,(p+2)%3+1)
print sprintf("%g %g %g", Px[tap1], Py[tap1], z)
print sprintf("%g %g %g", Center2x(tap1,tap2), Center2y(tap1,tap2), z)
print sprintf("%g %g %g", Center3x(tap1,tap2,tap3), Center3y(tap1,tap2,tap3), z)
print sprintf("%g %g %g", Center2x(tap1,tap3), Center2y(tap1,tap3), z)
print sprintf("%g %g %g", Px[tap1], Py[tap1], z)
print ''
}
}
set print
set label 1 "Coloring areas."
plot $QUADRANGLES u 1:2:3 w filledcurves closed lc palette, \
$EDGES u 1:2:3:4 w vec lw 1.0 lc "grey" nohead, \
$HULL u 1:2:3:4 w vec lw 1.5 lc "blue" nohead, \
$Data u 1:2:3 w p pt 7 ps 0.5 lc palette
### end of code
Result:
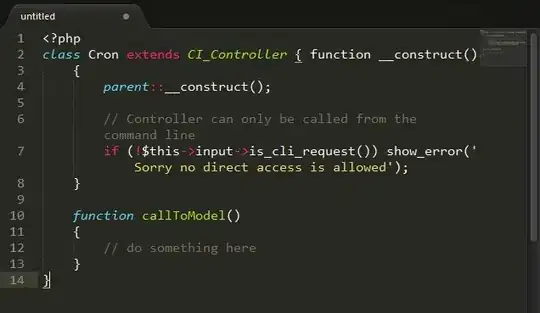
Animation: (in reality, it takes about 3 minutes on my old laptop)