How to create a polygon out of the outer cells of a contiguous patch of cells

Question

I have below a contiguous patch of cells plotted in Matlab.

The outer cells of the red patch have to be determined and then a polygon joining the centers of these cells will give me a polygon. How do i compute the outer cells of the contiguous patch?

I have an array of integers whose elements denote the cell in the red patch, for example,

a=[1;64;23;456;345];

Each element , say 64 corresponds to a cell in the image, and it is the cell belonging to the red patch.

The motivation to solve the problem is to deal with a polygon with minimal number of edges rather than so many cells. it slows down computation. Convex hull is not good enough. I don't want the resulting polygon to overlap with the brown area at all.

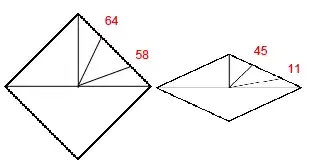
What i am suggesting is the case on the left in image below but it seems ugly. So a better way would be as in right to just skip the cells only sharing a single point with the outer brown area. I would like my outer cells to then be only those that share more than just a single point with the outer brown area.

But we want to avoid large number of edges in the resultant polygon!

Answer 1

I first processed the sample image from your question to create a logical mask (you already have an example of how to do that here).

Once you have this mask, there is a really easy way to generate the polygon you want using the bwtraceboundary function from the Image Processing Toolbox. This will give you a set of pixel indices in order around the perimeter of your masked region:

[r, c] = find(mask, 1);
coords = bwtraceboundary(mask, [r c], 'N');

And we can visualize it like so:

imagesc(mask);
colormap([0.9 0.9 0.9; 0.6 0.6 0.6]);
axis equal
set(gca, 'XLim', [0.5 0.5+size(mask, 2)], 'YLim', [0.5 0.5+size(mask, 1)]);
hold on;
plot(coords(:, 2), coords(:, 1), 'r', 'LineWidth', 2);
plot(coords(1, 2), coords(1, 1), 'go', 'LineWidth', 2);

The coordinates for the red line are ordered starting from the green circle and moving clockwise around the perimeter pixels of the masked region.

If you would prefer to generate a boundary outline that follows along the perimeter pixel edges of the region instead of the perimeter pixel centers, you can use the solution from my answer to a related question. This will yield the following:

Answer 2

Using Image Processing toolbox You can apply dilation on the image and than apply and operator between result of dilation and the original image.

A = imread('bnhfm.png');
B = A & imdilate(~A, true(3));
imshow(B);
imwrite(B, 'result.png');

Answer 3

Although the answer by @rahnema1 is really cool, I think the OP is asking more how to extract the set of edges according to the described rules.

Here is my approach identifying all the 10 patterns of 2x2 pixels that contain edges. Assuming the matrix A has the image with 1s and 0s (A = zeros(ny, nx); A(a) = 1):

% we identify patterns with edges over 2x2 patches, describing with
% the first 4 binary values what pixels are set, and with the next 2
% the edge with 2 indices over the 2x2 patch
patterns = [
 0,1,0,1,  3,4 % vertical edge at rhe right 
 1,0,1,0,  1,2 % vertical edge at the left
 0,0,1,1,  2,4 % horizontal edge at the bottom
 1,1,0,0,  1,3 % horizontal edge at the top
 1,0,0,1,  1,4 % diagonal edge
 0,1,1,0,  2,3 % diagonal edge
 1,0,1,1,  1,4 % diagonal edge, extra pixel set
 1,1,0,1,  1,4 % diagonal edge, extra pixel set
 1,1,1,0,  2,3 % diagonal edge, extra pixel set
 0,1,1,1,  2,3 % diagonal edge, extra pixel set
];

% 2x2 patches (matrix form)
P00 = A(1:end-1,1:end-1);
P10 = A(2:end,1:end-1);
P01 = A(1:end-1,2:end);
P11 = A(2:end,2:end);

% edge unique identifier using powers of 2
id = @(p00,p01,p10,p11) 1*p00 + 2*p10 + 4*p01 + 8*p11;
P = id(P00,P01,P10,P11); % vectorized pattern identification

% edges
e0 = []; % from (i,j)
e1 = []; % to (i,j)
for i = 1:size(patterns, 1) % small loop over the 10 patterns
  p = patterns(i, :);
  E = (P == id(p(1),p(2),p(3),p(4))); % pattern search, vectorized
  [c,r] = ind2sub(size(E), find(E));
  [c0,r0] = ind2sub([2,2], p(5));
  [c1,r1] = ind2sub([2,2], p(6));
  e0 = [e0; c+c0, r+r0];
  e1 = [e1; c+c1, r+r1];
end

And here the result applying it to your image (I used GIMP for capture, resize and filter, so maybe the image is not exactly the same):

X = [e0(:,2) e1(:,2)];
Y = size(A,1) - [e0(:,1) e1(:,1)];
plot(X', Y', '.-')

I am assuming that obtaining an ordered sequence of edges describing the polygon (or polygons) is not the main problem here once you have the aforementioned set.