Given a concave polygon (with no self-intersections), with its nodes in clockwise order, how can we determine all of its inner diagonals (those that are inside the polygon)?
I am interested in a solution that doesn't use any trig functions.
Background and what I tried:
In my computational geometry class we were given the following algorithm to test whether [pi, pj] is an inner diagonal in a polygon p0, p1, ... pn-1:
- Test if
[pi, pj]intersects an edge of the polygon that is not adjacent to it. If yes, it's not an inner diagonal. If not, go to step 2. - if
piis a convex point (pi-1, pi, pi+1make a right turn), then[pi, pj]is an inner diagonal iffpi, pj, pi+1andpi, pi-1, pjmake a left turn. - if
piis not a convex point (pi-1, pi, pi+1make a left turn), then[pi, pj]is an inner diagonal iffpj, pj-1, pimake a left turn.
- if
This algorithm was given to us for a triangulation algorithm involving ear-clipping. I implemented that algorithm and it seems to work fine there, but the catch is that the ear-clipping algorithm only uses diagonals of the form [pi, pi+2].
However, consider the brute force triangulation algorithm that selects all non-intersecting diagonals. Using what I described as a subroutine for checking inner diagonals (together with a segment intersection method), I get the following result:
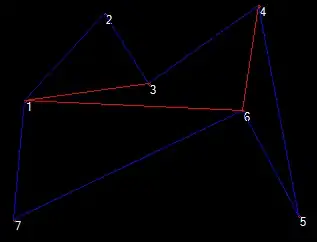
It's easy to check that the algorithm I posted rejects the inner diagonal [3, 6], when in fact it shouldn't:
3 is not a convex point, and 6, 5, 3 make a right turn instead of a left turn, so it gets rejected.
Note that, when using the ear-clipping algorithm, this polygon is triangulated correctly.
I am interested in how this algorithm can be adapted to detect all diagonals in a polygon. I've had no luck getting it to work.
I have also found other problems with this method, such as polygons for which exterior diagonals are drawn. Again, those work with the ear-clipping algorithm. We were never told that this method only applies for a special form of diagonals however, so I'm looking for clarifications.
Note: I couldn't decide whether to post this on math.stackexchange.com or here, since computational geometry deals in somewhat equal measure with both programming and mathematics, however I felt that programmers might be more familiar with this kind of algorithms than mathematicians, since someone has probably actually implemented this at some point.