Detect card MinArea Quadrilateral from contour OpenCV

Question

Yet another about detecting card in a picture. I've managed to pretty much isolate the card in the picture, I have a convex hull that is close and from here I'm stuck.

For the context/constraint, objective:

• Detect a card in a picture
• Plain-ish background (see example)
• Type of card fixed ahead (meaning: we have the width/height ratio)
• One object per picture (for now at least)

Approach I used:

1. Downscale
2. Gray-scale
3. Light Blur
4. Canny
5. Find contours
6. Remove all contours in list with less than 120 points (try/error value)
7. Case 1: I have 1 contour: perfect contour of my card: step 9
8. Case 2: I have multiple contour
   • Convex hull
   • Approximate polygon ?
9. ???

Step 1, 3 and 6 are mainly to remove noise and small artifacts.

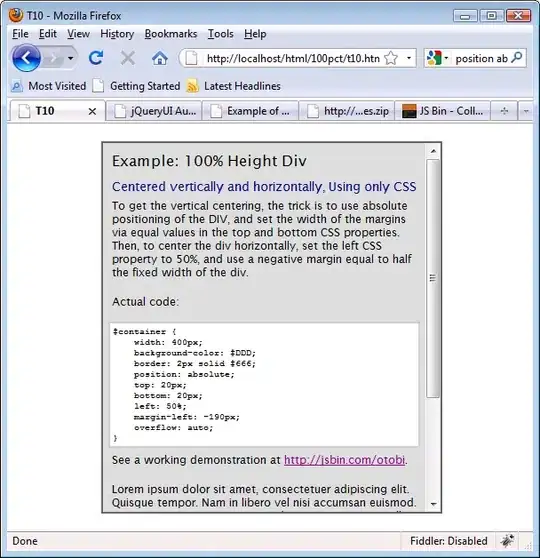
So I'm pretty much stuck at step 9. I've tried on a sample picture:

On the debug picture:

• Green: contours
• Red: convex hull
• Purple/Pink-ish: used approxPolyDp
• Yellow: minAreaRect

(the result image is extracted from the minAreaRect)

So the contour is acceptable, I can probably do a little better by tweaking the parameters from canny or the first blur. But for now this is acceptable, the issue now is, how can I get the the 4 points that will form the "minarea quadrilateral". As you can see, minAreaRect gives a rectangle which is not perfect, and the approxPolyDp is losing too much of the card.

Any clue how I can approach this? I tried playing with the epsilon value when using approxPolyDp (I used arcLength*0.1), but nothing.

Another issue with this approach is that is a corner is lost during canny (see example) it'll not work (unless when using minAreaRect). But this can probably be resolved before (with a better pre-processing) or after (since we know the width/height ratio).

Not asking for code here, just ideas how to approach this,

thanks!

Edit: Yves Daoust's solutions:

• Get the 8 points from the convex hull that match the predicate: (maximize x, x+y, y, -x+y, -x, -x-y, -y, x-y)
• From this octagon, take 4 longest sides, get the intersection points

Result:

Edit 2: Using Hough transform (instead of 8 extreme points) gives me better result for all cases where the 4 sides are found. If more than 4 lines are found, probably we have duplicates, so use some maths to try to filter and keep 4 lines. I coded a draft working by using the determinant (close to 0 if parallel) and the point-line distance formula)

Answer 1

Here is the pipeline I tried on your input image:

Step 1: Detect egdes

• Blur grayscale input and detect edges with Canny filter

Step 2: Find the card's corners

• Compute the contours
• Sort the contours by length and only keep the largest one
• Generate the convex hull of this contour
• Create a mask out of the convex hull
• Use HoughLinesP to find the 4 sides of your cards
• Compute the intersections of the 4 sides

Step 3: Homography

• Use findHomography to find the affine transformation of your card (with the 4 intersection points found at Step 2)
• Warp the input image using the computed homography matrix

And here is the result:

Note that you will have to find a way to sort the 4 intersection points so that there are always in the same order (otherwise findHomography won't work).

I know you didn't ask for code, but I had to test my pipeline so here it is... :)

Vec3f calcParams(Point2f p1, Point2f p2) // line's equation Params computation
{
    float a, b, c;
    if (p2.y - p1.y == 0)
    {
        a = 0.0f;
        b = -1.0f;
    }
    else if (p2.x - p1.x == 0)
    {
        a = -1.0f;
        b = 0.0f;
    }
    else
    {
        a = (p2.y - p1.y) / (p2.x - p1.x);
        b = -1.0f;
    }

    c = (-a * p1.x) - b * p1.y;
    return(Vec3f(a, b, c));
}

Point findIntersection(Vec3f params1, Vec3f params2)
{
    float x = -1, y = -1;
    float det = params1[0] * params2[1] - params2[0] * params1[1];
    if (det < 0.5f && det > -0.5f) // lines are approximately parallel
    {
        return(Point(-1, -1));
    }
    else
    {
        x = (params2[1] * -params1[2] - params1[1] * -params2[2]) / det;
        y = (params1[0] * -params2[2] - params2[0] * -params1[2]) / det;
    }
    return(Point(x, y));
}

vector<Point> getQuadrilateral(Mat & grayscale, Mat& output) // returns that 4 intersection points of the card
{
    Mat convexHull_mask(grayscale.rows, grayscale.cols, CV_8UC1);
    convexHull_mask = Scalar(0);

    vector<vector<Point>> contours;
    findContours(grayscale, contours, RETR_EXTERNAL, CHAIN_APPROX_NONE);

    vector<int> indices(contours.size());
    iota(indices.begin(), indices.end(), 0);

    sort(indices.begin(), indices.end(), [&contours](int lhs, int rhs) {
        return contours[lhs].size() > contours[rhs].size();
    });

    /// Find the convex hull object
    vector<vector<Point> >hull(1);
    convexHull(Mat(contours[indices[0]]), hull[0], false);

    vector<Vec4i> lines;
    drawContours(convexHull_mask, hull, 0, Scalar(255));
    imshow("convexHull_mask", convexHull_mask);
    HoughLinesP(convexHull_mask, lines, 1, CV_PI / 200, 50, 50, 10);
    cout << "lines size:" << lines.size() << endl;

    if (lines.size() == 4) // we found the 4 sides
    {
        vector<Vec3f> params(4);
        for (int l = 0; l < 4; l++)
        {
            params.push_back(calcParams(Point(lines[l][0], lines[l][1]), Point(lines[l][2], lines[l][3])));
        }

        vector<Point> corners;
        for (int i = 0; i < params.size(); i++)
        {
            for (int j = i; j < params.size(); j++) // j starts at i so we don't have duplicated points
            {
                Point intersec = findIntersection(params[i], params[j]);
                if ((intersec.x > 0) && (intersec.y > 0) && (intersec.x < grayscale.cols) && (intersec.y < grayscale.rows))
                {
                    cout << "corner: " << intersec << endl;
                    corners.push_back(intersec);
                }
            }
        }

        for (int i = 0; i < corners.size(); i++)
        {
            circle(output, corners[i], 3, Scalar(0, 0, 255));
        }

        if (corners.size() == 4) // we have the 4 final corners
        {
            return(corners);
        }
    }
    
    return(vector<Point>());
}

int main(int argc, char** argv)
{
    Mat input = imread("playingcard_input.png");
    Mat input_grey;
    cvtColor(input, input_grey, CV_BGR2GRAY);
    Mat threshold1;
    Mat edges;
    blur(input_grey, input_grey, Size(3, 3));
    Canny(input_grey, edges, 30, 100);

    vector<Point> card_corners = getQuadrilateral(edges, input);
    Mat warpedCard(400, 300, CV_8UC3);
    if (card_corners.size() == 4)
    {
        Mat homography = findHomography(card_corners, vector<Point>{Point(warpedCard.cols, 0), Point(warpedCard.cols, warpedCard.rows), Point(0,0) , Point(0, warpedCard.rows)});
        warpPerspective(input, warpedCard, homography, Size(warpedCard.cols, warpedCard.rows));
    }

    imshow("warped card", warpedCard);
    imshow("edges", edges);
    imshow("input", input);
    waitKey(0);

    return 0;
}

EDIT: I've have tweaked a little the parameters of Canny and HoughLinesP functions to have a better detection of the card (program now works on both input samples).

Answer 2

As the object is isolated on a uniform background, I would recommend to start finding edges from the image outline, towards the center, and stop at the first edge points met.

Unless you get false positives in the background area, the convex hull will give you a fairly good approximation of the object outline, despite edge point misses.

Now to get the bounding quadrilateral, you can find the farthest points in the eight cardinal directions (maximize x, x+y, y, x-y, -x, -x-y, -y, -x+y). This gives you an octagon (possibly with merged vertices). Take the four longest sides and intersect them to find the corners.