My question stems from the observation made that we can use a Linear Feedback Shift Register to perform a CRC check. Algebraically this normally is of the form;
S(x) = M(x) * x^k % G(x) ( gives the remainder, for a G(x) of order k)
The implementation of this is shown in this question, (and registers are all initialised to zero) and the mathematical bitwise calculation of the XOR division is shown in this question here.
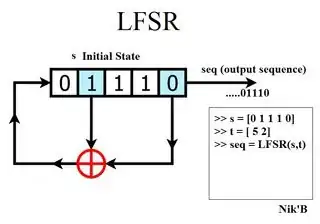
I understand both of these - however, I also know that another common way of using an LFSR is to have no input, but instead preload the registers with non-zero values, and run (with zero as an input) to form a sequence of pseudo random numbers. This is shown in the image below
My question is, just as the CRC can be represented as a modulo-2 division both bitwise and algebraically, can we do the same for an LFSR sequence generator, given the generator polynomial and initial values? And if so, an example would be great!
Thanks very much, feel free to correct me if I've misrepresented or misunderstood a concept!