This is a continuation of some questions I posed earlier, How to plan the most efficient route for patio lights and Christmas Light Route Efficiency (CS), about my attempt to cover a screened-in structure with patio lights as efficiently as possible.
Here's the rules:
- Minimize light overlapping
- Each string of lights is 234" long (this is important because I can't start a new branch of lights unless it's at the end of another branch).
Think of these as Christmas lights, you have a male and a female side:
start (male) end (female) =[}~~~o~~~o~~~o~~~o~~~o~~~o~~~o~~~{=] <- to outlet to other lights ->So multiple strands can daisy chain as long as there's a female for the male to plug into, like this:
A female plug must supply power to the next strand of lights via a male plug, a male plug can't give power to another male plug.
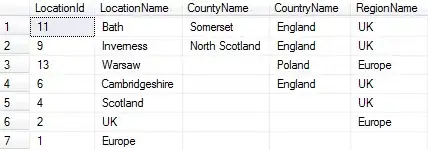
Here is a diagram of my structure:
Pink Circle = Place to hang lights (No, there is not a place to hang lights at the intersection of 10, 11 & 12 - that is not a mistake).
- "Start" = The only available electrical outlet.
- Yellow Dots = Parts of the structure I want to run the lights along.
Based on my previous questions, I began looking into "Route Efficiency Problem" Algorithms. I used this post, Solving Chinese Postman algorithm with eulerization, to get started, which lead me to this code (with thanks to @DamianoFantini for his help in my previous post to set the graph up correctly):
gg <- graph_from_edgelist(cbind(c(1:4, 6, 8, 10, 12, 14, 16:19, 1, 6, 8, 21, 12, 14, 5, 7, 9, 11, 13, 15),
c(2:5, 7, 9, 11, 13, 15, 17:20, 6, 8, 10, 12, 14, 16, 7, 9, 11, 13, 15, 20)))
ll=matrix(
c( 0,0, 75.25,0, 150.5,0, 225.8125,0, 302.8125,0,
0,-87, 302.8125,-87,
0,-173.8125, 302.8125,-173.8125,
0,-260.9375, 302.8125,-260.9375,
16,-384.3125, 302.8125,-384.3125,
16,-435.9575, 302.8125,-435.9375,
16,-525.1875, 75.25,-525.1875, 150.5,-525.1875, 225.8125,-525.1875, 302.8175,-525.1875, 16, -260.9375),
ncol=2,byrow=TRUE)
# SOURCE: https://stackoverflow.com/q/40576910/1152809
make.eulerian <- function(graph){
# Carl Hierholzer (1873) had explained how eulirian cycles exist for graphs that are
# 1) connected, and 2) contain only vertecies with even degrees. Based on this proof
# the posibility of an eulerian cycle existing in a graph can be tested by testing
# on these two conditions.
#
# This function assumes a connected graph.
# It adds edges to a graph to ensure that all nodes eventuall has an even numbered. It
# tries to maintain the structure of the graph by primarily adding duplicates of already
# existing edges, but can also add "structurally new" edges if the structure of the
# graph does not allow.
# save output
info <- c("broken" = FALSE, "Added" = 0, "Successfull" = TRUE)
# Is a number even
is.even <- function(x){ x %% 2 == 0 }
# Graphs with an even number of verticies with uneven degree will more easily converge
# as eulerian.
# Should we even out the number of unevenly degreed verticies?
search.for.even.neighbor <- !is.even(sum(!is.even(degree(graph))))
# Loop to add edges but never to change nodes that have been set to have even degree
for(i in V(graph)){
set.j <- NULL
#neighbors of i with uneven number of edges are good candidates for new edges
uneven.neighbors <- !is.even(degree(graph, neighbors(graph,i)))
if(!is.even(degree(graph,i))){
# This node needs a new connection. That edge e(i,j) needs an appropriate j:
if(sum(uneven.neighbors) == 0){
# There is no neighbor of i that has uneven degree. We will
# have to break the graph structure and connect nodes that
# were not connected before:
if(sum(!is.even(degree(graph))) > 0){
# Only break the structure if it's absolutely nessecary
# to force the graph into a structure where an euclidian
# cycle exists:
info["Broken"] <- TRUE
# Find candidates for j amongst any unevenly degreed nodes
uneven.candidates <- !is.even(degree(graph, V(graph)))
# Sugest a new edge between i and any node with uneven degree
if(sum(uneven.candidates) != 0){
set.j <- V(graph)[uneven.candidates][[1]]
}else{
# No candidate with uneven degree exists!
# If all edges except the last have even degrees, thith
# function will fail to make the graph eulerian:
info["Successfull"] <- FALSE
}
}
}else{
# A "structurally duplicated" edge may be formed between i one of
# the nodes of uneven degree that is already connected to it.
# Sugest a new edge between i and its first neighbor with uneven degree
set.j <- neighbors(graph, i)[uneven.neighbors][[1]]
}
}else if(search.for.even.neighbor == TRUE & is.null(set.j)){
# This only happens once (probably) in the beginning of the loop of
# treating graphs that have an uneven number of verticies with uneven
# degree. It creates a duplicate between a node and one of its evenly
# degreed neighbors (if possible)
info["Added"] <- info["Added"] + 1
set.j <- neighbors(graph, i)[ !uneven.neighbors ][[1]]
# Never do this again if a j is correctly set
if(!is.null(set.j)){search.for.even.neighbor <- FALSE}
}
# Add that a new edge to alter degrees in the desired direction
# OBS: as.numeric() since set.j might be NULL
if(!is.null(set.j)){
# i may not link to j
if(i != set.j){
graph <- add_edges(graph, edges=c(i, set.j))
info["Added"] <- info["Added"] + 1
}
}
}
# return the graph
(list("graph" = graph, "info" = info))
}
# Look at what we did
eulerian <- make.eulerian(gg)
g <- eulerian$graph
par(mfrow=c(1,2))
plot(gg)
plot(g)
Here's the result of the code:
Which, I think translates to this (but I am a graph/algorithm noob, so correct me if I'm wrong):
Obviously, there are some issues here:
- I have no idea where the end/beginning of each strand of lights should be (and neither does the algorithm I think)
- Node 1 is supplying power independently. This will not work in reality. All power must come from the "Start" position.
- The distances and structure do not seem to be accounted for.
Is there a way to add these constraints into the algorithm? Is there another algorithm I could use that would make this easier?