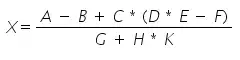Recursive algorithm fails to complete tests in allotted time

Question

I was doing a test that required an algorithm for Binary Tomography. A set of 38 test values are supplied that test correctness, but there is also a time limit of 1 CPU sec to complete all the tests. The problem is as follows:

Output “Yes” if there exists an m-by-n matrix A, with each element either being 0 or 1, such that

Otherwise output “No”.

For each test, 2 arrays are provided:

1. r (the sum of each row in the matrix)
2. c (the sum of each column in the matrix)

In the equation:

• m is the length of the r array, where 1 <= m
• n is the length of the c array, where n <= 1000
• ri is an element of r, where 0 <= ri <= n
• cj is an element of c, where 0 <= cj <= m

A "Yes" example

m = 3; n = 4; r = [2, 3, 2]; c = [1, 1, 3, 2];

A "No" example

m = 3; n = 3; r = [0, 0, 3]; c = [0, 0, 3];

I have a solution that appears to give correct answers, however it only manages 12 / 38 tests before the 1 second of CPU time is exceeded.

I originally wrote the code in ES5 and then went back and converted to to ES3 to try and get more performance out of it. (originally managed 9 tests as ES5). There doesn't seem a great deal left that I can do to the current algorithm to improve the performance (unless I am mistaken). This leads me to believe that my algorithm is at fault an that there must be a faster algorithm for doing this. I did a ton of reading trying to find one and ended up with a headache :)

So I'm turning to the community to see if anyone can suggest a faster algorithm than I am currently using.

'use strict';

const ZEROS = (function (seed) {
  let string = seed;
  for (let i = 0; i < 19; i += 1) {
    string += seed;
  }

  return string;
}('00000000000000000000000000000000000000000000000000'));

const ZEROSLEN = ZEROS.length;

const permutate = function (n, ri) {
  const result = [];
  const memoize = {};
  let count = 0;
  do {
    const bin = count.toString(2);
    if (ZEROSLEN + bin.length > ZEROSLEN + n) {
      break;
    }

    if (!memoize[bin] && (bin.split('1').length - 1) === ri) {
      const string = (ZEROS + bin).slice(-n);
      const sLen = string.length;
      const perm = new Array(sLen);
      for (let i = sLen - 1; i >= 0; i -= 1) {
        perm[i] = +string[i];
      }

      memoize[bin] = result.push(perm);
    }

    count += 1;
  } while (count);

  return result;
};

const getMatrixSum = function (n, matrix) {
  const mLength = matrix.length;
  const rows = new Array(mLength);
  const a = new Array(n);
  const last = mLength - 1;
  for (let x = n - 1; x >= 0; x -= 1) {
    for (let y = last; y >= 0; y -= 1) {
      rows[y] = matrix[y][x];
    }

    let sum = 0;
    for (let i = rows.length - 1; i >= 0; i -= 1) {
      sum += rows[i];
    }

    a[x] = sum;
  }

  return a;
};

const isEqual = function (a, b) {
  const length = a.length;
  if (length !== b.length) {
    return false;
  }

  for (let i = length - 1; i >= 0; i -= 1) {
    if (a[i] !== b[i]) {
      return false;
    }
  }

  return true;
};

const addRow = function (i, prev, r, c, result) {
  if (result) {
    return result;
  }

  const n = c.length;
  const ri = r[i];
  if (ri < 0 || ri > n) {
    throw new RangeError('ri out of range');
  }

  const p = permutate(n, ri);
  const m = r.length;
  const rsLast = m - 1;
  const nextI = i + 1;
  for (let x = p.length - 1; x >= 0; x -= 1) {
    const permutation = p[x];
    const next = prev.slice();
    next.push(permutation);
    const sums = getMatrixSum(n, next);
    if (i < rsLast) {
      let memo = 0;
      for (let j = sums.length - 1; j >= 0; j -= 1) {
        if (sums[j] > c[j]) {
          memo += 1;
        }
      }

      if (!memo && addRow(nextI, next, r, c, result)) {
        return true;
      }
    } else if (isEqual(sums, c)) {
      return true;
    }
  }

  return false;
};

const isSolvable = function (r, c) {
  const m = r.length;
  const n = c.length;
  if (m < 1 || n > 1000) {
    throw new Error('Bad data');
  }

  for (let j = n; j >= 0; j -= 1) {
    const cj = c[j];
    if (cj < 0 || cj > m) {
      throw new RangeError('cj out of range');
    }
  }
  
  return addRow(0, [], r, c, false) ? 'Yes' : 'No';
};

console.log(isSolvable([2, 3, 2], [1, 1, 3, 2]));

console.log(isSolvable([0, 0, 3], [0, 0, 3]));

It may be worth noting that the tests are being run on SpiderMonkey version JavaScript-C24.2.0

Refs:

https://en.wikipedia.org/wiki/Discrete_tomography

https://open.kattis.com/problems/tomography

Answer 1

Since permutations yield to brute force, they should be the last resort when developing algorithms similar to this one. Most of the time they are not needed.

As i have commented above, I have a feeling that one strategy could be first sorting the r and c arrays descending and start with the bigger ones. I haven't had time to implemented a JS code to work out this, so I haven't had a chance to test thoroughly. Please have a look and if you discover a flaw please mention.

In the below visual representation of the algorithm we try r = [1,3,1,3] and c = [3,2,1,2]. X denotes an occupied cell and a red dot denotes an untouchable cell while the empty ones are obviously the free cells. So in the real algorithm to represent a cell we need a data type like {value: false, avail: false} for a red dot while {value: false, avail: true} would mean a free space. Or to save space and speed you may use a data type like 0b00 for red dot, 0b01 for free space and 0b1X for occupied (X here means don't care) cells.

Note: It's worth mentioning Step 3 where we process c[0]. After we insert the three Xs we have to check the rows occupied by the Xs to update the status of the empty cells in those rows. In this case for r[2], all empty cells become untouchable.

Edit:

Well.. OK since we don't need to construct the solution in a 2D array like structure but only need an answer on wheather the supplied data is meaningful or not, I have come up with another and simpler idea which is essentially based on the above approach. I really don't think it can get any faster than this. It solves a 999 by 1000 board in like 50ms.

Lets get into it.

1. The input is r = [2, 3, 2]; c = [1, 1, 3, 2]; However one important condition here is both c and r arrays should sum up to the same number. We can simply check this at the beginning of our code or leave it, go through the following steps and if they pass check only if c is full of 0s. The following code prefers the latter approach.
2. Sort r descending so; r = [3, 2, 2]; c = [1, 1, 3, 2];
3. Try reducing r[0] (3 in the first case) many non-zero elements of c by 1. Now c becomes [0, 0, 2, 2]. If it fails then try no more and return false.
4. Now that we have finished with row r[0], recursivelly call function with r = [2, 2]; c = [0, 0, 2, 2]; while r.length is bigger than 0 and the bool argument b is true. Next call will be r = [2]; c = [0, 0, 1, 1]; and finally r = []; c = [0, 0, 0, 0];
5. If finally a recursive call with empty r is invoked then check b is true and all items of c are 0. (b && cs.every(n => !n)).

I believe this is just fine but as i don't have your test cases it's for you to try. I am sure it will pass the time test though. Here is the code in it's simplest. Here i am testing rs = [7,3,5,4,6,2,8] and cs = [7,1,6,3,4,5,2,7]. It looks like;

  71634527
7 x xxxxxx
3 x x    x
5 x x xx x
4 x x  x x
6 x xxxx x
2 x      x
8 xxxxxxxx

function nonogram(rs,cs){
  function runner(rs,cs, b = true){//console.log(rs,cs,b)
    return b && rs.length ? runner(rs.slice(1),                                 // rows argument
                                   cs.map(e => rs[0] ? e ? (b = !--rs[0], e-1)  // cols argument
                                                         : e
                                                     : e),
                                   b)                                           // bool argument
                          : b && cs.every(n => !n);
  }
return runner(rs.sort((a,b) => b-a), cs);
}

var rs = [7,3,5,4,6,2,8],
    cs = [7,1,6,3,4,5,2,7],
    result;
console.time("test");
result = nonogram(rs,cs);
console.timeEnd("test");
console.log(result);

Answer 2

I didn't have this ready for my test, but I found a far more efficient algorithm after the event.

'use strict';

const sortNumber = function (a, b) {
  return b - a;
};

const isSolvable = function (r, c) {
  const m = r.length;
  const n = c.length;
  if (m < 1 || n > 1000) {
    throw new Error('Bad data');
  }

  for (let j = n; j >= 0; j -= 1) {
    const cj = c[j];
    if (cj < 0 || cj > m) {
      throw new RangeError('cj out of range');
    }
  }

  while (r.length) {
    c.sort(sortNumber);
    const ri = r.pop();
    if (ri < 0 || ri > n) {
      throw new RangeError('ri out of range');
    }

    if (ri) {
      if (!c[ri - 1]) {
        return 'No';
      }

      for (let j = ri - 1; j >= 0; j -= 1) {
        c[j] -= 1;
      }
    }
  }

  for (let j = n - 1; j >= 0; j -= 1) {
    if (c[j]) {
      return 'No';
    }
  }

  return 'Yes';
};

console.log(isSolvable([2, 3, 2], [1, 1, 3, 2]));

console.log(isSolvable([0, 0, 3], [0, 0, 3]));